
| Gordon S. Novak Jr. | William C. Bulko |
| Department of Computer Sciences | IBM Corporation |
| University of Texas at Austin | 11400 Burnett Road |
| Austin, Texas 78712 | Austin, Texas 78758 |
Copyright © 1990 by AAAI Press.
This article appears in Proc. National Conference on Artificial Intelligence (AAAI-90), Aug. 1990, pp. 465-470.
We describe a program, BEATRIX, that can understand textbook physics problems specified by a combination of English text and a diagram. The result of the understanding process is a unified internal model that represents the problem, including information derived from both the English text and the diagram. The system is implemented as two opportunistic co-parsers, one for English and one for diagrams, within a blackboard architecture. A central problem is establishing coreference, that is, determining when parts of the text and diagram refer to the same object. Constraints supplied by the text and diagram mutually reduce ambiguity in interpretation of the other modality.
Natural language is a versatile means of communication, but it is difficult to describe complex spatial relationships using natural language. Diagrams are frequently used to supplement natural language when spatial relationships need to be described. One of us has previously written a program that could understand textbook physics problems stated in English [novak:isaac,novak:ijcai]; however, most textbook physics problems are specified by a combination of English text and a diagram, neither of which is a complete description by itself. In understanding such a problem, the human reader must produce a single, unified model of the problem that incorporates information from both input modalities; to do so, it is essential to establish coreference, that is, to determine when different forms of description refer to the same object in the situation that is being described and, therefore, in the model of the situation that is being constructed by the reader.
Both natural language and diagrams can be highly ambiguous. A line in a diagram might represent an edge of a large object (such as the surface of the earth), part of a single object, a shared boundary between two objects, or an object in itself (such as a cable). Ambiguity can be reduced by knowing what things are expected to be in the diagram from reading the English text. As some objects are identified, the set of possible identifications of the remaining objects is reduced. Inferences based on common-sense physical principles can further reduce ambiguity; for example, an object is expected to be supported by something, and a rope is expected to be attached to something. Understanding the diagram can likewise reduce ambiguity in interpretation of the English description.
The process of understanding text and diagram together must be opportunistic: it is important to use all the clues that are available, but it is not possible to predict which clues will be present for a particular problem or what order of interpretation will cause all the pieces to fall into place. For this reason, the BEATRIX system [bulko:diss,bulko88] has been implemented within a blackboard architecture, using the BB1 blackboard system [bb1-manual] and GLISP [novak:glisp].
Examples of the kinds of problems understood by BEATRIX are shown in Figures 1 and 2. The result of the understanding process is a representation of the problem suitable for input to a physics problem solver such as that of Kook [kook:diss,kook-novak].

((TWO MASSES ARE CONNECTED BY A LIGHT STRING
AS SHOWN IN THE FIGURE)
(THE INCLINE AND PEG ARE SMOOTH)
(FIND THE ACCELERATION OF THE MASSES AND
THE TENSION IN THE STRING FOR
THETA = 30 DEGREES AND M1 = M2 = 5 KG))
Fig. 1: Test Problem P3 (Tipler 11)

((TWO MASSES ARE CONNECTED BY A CABLE AS
SHOWN IN THE FIGURE)
(THE STRUT IS HELD IN POSITION BY A CABLE)
(THE INCLINE IS SMOOTH , AND THE CABLE
PASSES OVER A SMOOTH PEG)
(FIND THE TENSION IN THE CABLE FOR
THETA = 30 DEGREES AND M1 = M2 = 20 KG)
(NEGLECT THE WEIGHT OF THE STRUT))
Fig. 2: Test Problem A2
Diagrams are entered by means of a user interface that allows drawings to be constructed easily by selecting drawing components and moving, scaling, and rotating them as desired. The interface also allows entry of bits of text within the diagram, as well as entry and editing of the English problem statement. The drawing is displayed in a window as it is constructed. As a side effect, a symbolic description of the items in the diagram is constructed; it is this description that serves as input to the understanding program.
If the input to the diagram understander were in terms of components such as blocks, ropes, and pulleys, understanding it would be trivial. Instead, we have taken care to make the input consist of ``neutral'' components such as lines, circles, and rectangles -- a form of input that could reasonably be produced automatically from a printed diagram by a vision preprocessor [ballard-brown]. Diagram items are represented by property-value pairs; for example,
(class LINE endpt1 (129 . 142)
endpt2 (354 . 173)
dashed T ah1 T ah2 NIL)
represents a dashed line with an arrowhead at its first endpoint
(ah1).
A human who is solving a physics problem will not read all of the text, and only then look at the diagram, or vice versa; instead, the human will typically look briefly at the picture, read some text, look back at the picture, and so forth until the problem has been understood. It is unlikely that any fixed order of processing would suffice for a broad selection of problems, especially since a given problem could be specified entirely by text, entirely by a diagram, or by a combination of the two. For this reason, BEATRIX is organized using co-parsing of the two input modalities. Parsing of the English text and parsing of the diagram proceed in parallel; the final interpretation of objects takes into account information from both parsed text and parsed diagram. This kind of control strategy allows understanding to be opportunistic, taking advantage of clues to understanding that arise from diverse knowledge sources; such a control strategy has been found to be advantageous in other perceptual domains such as speech understanding [hearsay] and sonar signal interpretation [nii:hasp].
The domain blackboard of the system is organized into five levels, as shown in Figure 3.

Fig. 3: Domain Blackboard Organization
The lowest levels of the blackboard are called TEXT and PICTURE . TEXT contains the English sentences of the problem statement; each sentence has a sequence number indicating its order of occurrence. PICTURE contains symbolic descriptions of the diagram elements, such as BOX, LINE, or CIRCLE. In addition, the PICTURE level contains a set of objects created by a preprocessor that represent contact points between diagram elements.
The intermediate blackboard levels, TEXT-MODEL and PICTURE-MODEL, represent hypotheses created by the parsing of the text and diagram. Objects on the PICTURE-MODEL level represent elementary physical objects, such as MASS or PULLEY, that are possibly contained in the diagram; these are recognized independently from the text, before coreference resolution takes place. TEXT-MODEL objects represent physical objects and relations tentatively identified from the TEXT by the English parser.
The most abstract level of the blackboard is the PROBLEM-MODEL level. Objects at this level represent physical objects in the final interpretation of the problem; these objects have links connecting them to their corresponding objects on the TEXT-MODEL and PICTURE-MODEL levels.
BEATRIX contains 53 knowledge sources ( KS's); each is a specialist in understanding a particular part of a problem description. Table 1 shows the knowledge sources used and classifies them into groups. The Control KS, Define-Reliability, is used to set up code for calculating execution priorities of the other KS's. The Identify KS's operate between the PICTURE and PICTURE-MODEL levels; they perform syntactic recognition of related groups of diagram elements. The single Parse KS calls an ATN parser written in Lisp to parse the sentences of the English text. Match KS's perform coreference matching, finding objects on the PICTURE-MODEL and TEXT-MODEL that correspond and making objects on the PROBLEM-MODEL level that encompass them. KS's whose names begin with Retrieve- serve to move information to higher levels of the blackboard when other KS's fail to do so, such as when an object appears in the diagram but is not mentioned in the text. Semantic KS's modify existing objects and make inferences; for example, if the angle between a horizontal surface and another surface is known, Propagate-Angle-ROTN will cause the rotation of the other surface to correspond to that angle. Of the Special KS's, Post-the-Problem initiates blackboard action by placing the text and diagram on their respective blackboard levels; the remaining KS's perform default reasoning for those cases where no more specific KS was able to act.
| Control: | Match: |
| Define-Reliability | Match-Incline |
| Match-Mass-to-Mass | |
| Identify: | Match-Mass-to-Object |
| Identify-Angles | Match-Normal-Arrow |
| Identify-Arrows | Match-Normal-Force |
| Identify-Line | Match-Pivot |
| Identify-Mass-Labels | Match-Pulley |
| Identify-Masses | Match-Rope |
| Identify-Pulley | Match-Struts |
| Identify-Pulley-System | Match-Surface |
| Identify-Struts | Match-Tension |
| Identify-Surfaces | Match-Tension-Arrow |
| Propagate-Touches | Match-Variable |
| Propagate-PM-Contact | |
| Parse: | Propagate-PSt-Contact |
| Parse-the-Sentences | Propagate-RM-Contact |
| Propagate-RP-Contact | |
| Semantic: | Propagate-RS-Contact |
| Add-Contact-Locs | Propagate-RSt-Contact |
| Add-Contact-Objects | Propagate-SM-Contact |
| Assign-Value-to-Variable | Propagate-SP-Contact |
| Correct-Floor-to-Table | Propagate-SS-Contact |
| Find-COEF | Propagate-SSt-Contact |
| Get-Mass-Value | |
| Neglect-TM-Weight | Special: |
| Propagate-Angle-ROTN | Default-Mass-ROTNs |
| Propagate-Rope-ROTN | Default-Rope-ROTNs |
| Propagate-Touch-ROTN | Post-the-Problem |
| Translate-BE-ADJ | Retrieve-Mass |
| Translate-LET-BE | Retrieve-Pulley |
| Retrieve-Rope | |
English sentences are parsed using an augmented transition network grammar [woods:atn] written in a meta-language similar to that described by Charniak and McDermott [charniak-mcdermott]. Figure NPcode shows the grammar function for a noun phrase; the grammar is simple and defers most semantic processing to the understanding module that considers text and diagram together. The ATN parser is invoked by a single knowledge source, Parse-the-Sentences. A sentence is syntactically parsed top-down, resulting in a parse tree and a list of tokens of the objects mentioned in the sentence on the TEXT-MODEL blackboard level. This forms the natural language input to the understanding module, which performs semantic processing of the natural language input and diagram together.
(DEFINEQ (NP (LAMBDA ()
(CHAIN NP
(EITHER
(CAT QWORD)
(SEQ (OPTIONAL (CAT DET))
(OPTIONAL (CAT NUMBER))
(OPTIONAL* (CAT ADJ))
(OPTIONAL (MEAS))
(CAT NOUN)
(SETQ NN1 (THAT NOUN))
(OPTIONAL (AND (SETQ LABEL-ARC
(CAT NOUN))
(EQ (GETPROP
(THAT NOUN)
'TYPE))
'VARIABLE)
LABEL-ARC))
(OPTIONAL (VCLAUSE))
(OPTIONAL (PREPP NN1)))))))
Fig. 4: Noun Phrase ATN Grammar Function NP
The diagram is parsed by a set of knowledge sources that recognize combinations of picture elements that have special meaning. In effect, these KS's act as grammar productions of a picture grammar [ksfu74]; [hanson78] describes the use of a blackboard system for scene interpretation that uses a grammar-like representation of components of a scene.
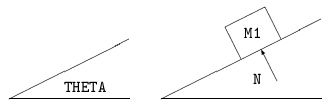
Local analysis of combinations of diagram elements often allows a combination to be interpreted as a larger and meaningful grouping. For example, if two lines touch at an acute angle and contain text between the lines and close to the vertex, and the text is a number or is a variable name that is typically used to denote an angle (such as THETA), then the two lines will be collected on the PICTURE-MODEL level as an ANGLE, and the number or variable will be associated with the ANGLE as its magnitude. An arc connecting the two lines is associated with the ANGLE if present, but is not required. The following examples show two angles, one containing text that is not part of the angle.
As parts of the diagram are interpreted, they trigger additional KS's that are associated with the interpretations. For example, after a small circle with a line to its center is interpreted as a PULLEY, the KS Identify-Pulley-System is triggered to look for the lines tangent to the pulley that represent the rope passing around the pulley. This results in the two lines that represent the rope being collected as a single ROPE object, with their endpoints away from the pulley being identified as the ends of the rope. This, in turn, triggers additional inferences, since the ends of a rope are expected to be attached to objects or surfaces. When a KS can make a clear interpretation of a part of the diagram, it obviates other KS's involving alternative interpretations of the object that might have been triggered.
In addition to triggering interpretations of other parts of the diagram, the diagram parsing KS's trigger expectations for later stages of processing. For example, identification of a CONTACT between a mass and a surface sets up an expectation that a normal force and coefficient of friction for the CONTACT may be specified by the English text.
The process of diagram ``parsing'' continues until no further interpretations can be made at that level; this results in a substantial degree of interpretation of the diagram. Figure 5 schematically illustrates the interpretation of an example after diagram parsing; most of the TOUCH relations and some CONTACT relations are omitted for readability.
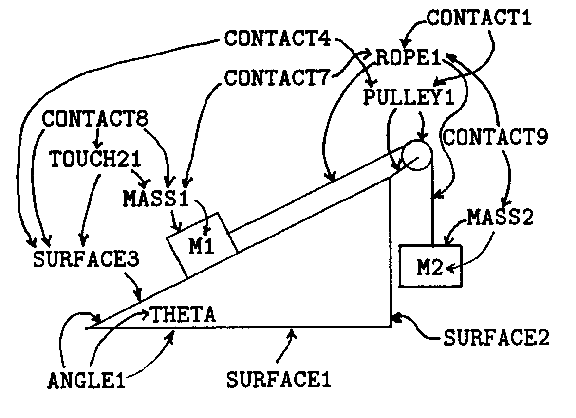
Fig. 5: Interpretation after Diagram Parsing
The understanding module controls the parsing of the text and diagram and performs the majority of the semantic processing. Its inputs are the ``parsed'' diagram on the PICTURE-MODEL level of the blackboard and the parsed sentences, represented as semantic networks or case frames, on the TEXT-MODEL level. It produces as output a unified model of the problem, incorporating information from both modalities.
In order to produce a unified model, a major task is to establish coreference between the two input modalities. Each object that appears in either text or diagram must be present on the PROBLEM-MODEL blackboard level; if features of an object appear in both text and diagram, the features must be collected on the same object in the model, to which the text and diagram co-refer. For example, the text could say ``the coefficient of friction is 0.25'', referring to a contact between a block and an inclined plane that is shown in the diagram but not mentioned in the text. In order to correctly understand the problem, the friction value from the text must be associated in the problem model with the contact relation between block and plane that was derived from the diagram.
The knowledge sources ( KS's) that perform coreference resolution are triggered when their corresponding types of objects are posted on the PICTURE-MODEL or TEXT-MODEL blackboard levels. For example, in the problem shown in Figure example1, parsing the phrase ``the string'' will cause an object representing the string to be added to the TEXT-MODEL level, and this will trigger the Match-Rope KS to attempt to find a corresponding object in the PICTURE-MODEL. In some cases, establishing coreference is fairly trivial, such as resolving a reference to ``the mass'' when only one item that could be a mass is present in the diagram. In other cases, however, the presence of parsed diagram elements on PICTURE-MODEL is necessary to resolve the referent of a phrase that would otherwise be incoherent. The text may contain a definite reference to an object (``the incline'') or to a feature of a relationship (``the coefficient of friction'') that is not otherwise mentioned in the text and could not be understood properly without the presence of the corresponding elements from the diagram. In effect, forward inferences are made to attempt to match things that might occur in the other modality; for example, in Figure example1 the contact between the mass and the inclined plane in the diagram causes the KS's Match-Normal-Force and Find-COEF to be triggered to look for corresponding references that might appear in the text.
The KS's of the understanding module also perform inferences that flesh out the representation of the problem; in some cases these can be considered to be based on common-sense physics. For example, BEATRIX will infer that the rotation of an object is the same as the rotation of the object on which it rests and that an object that is hanging from a rope hangs directly below it. Contact between an object and a surface is assumed to be a frictional touch contact, while contact between a rope and an object it supports is assumed to be an attachment. Such inferences are important for understanding, since natural language text often omits things that an intelligent reader is assumed to be able to infer.
Control of processing in understanding text and diagrams must be flexible, since no fixed order of processing is likely to succeed for a wide variety of problems. Some problems contain all of the necessary information in the text; for example, ISAAC [novak:isaac] handled problems that had diagrams in the textbooks from which they were taken, but had English descriptions sufficiently complete that diagram understanding was not necessary. Other problems rely heavily on the diagram; for example, in one example handled by BEATRIX the entire text is: ((WHAT IS THE TENSION IN THE CORD IN THE FIGURE)).
Control needs to be opportunistic, so that clear identifications can be made first; as some identifications are made, others that had been ambiguous often can be resolved uniquely. Expectations must be posted so that they can be matched with corresponding references that will appear later. Defaults need to be performed when no other knowledge source can operate.
A blackboard architecture provides a scheduling mechanism that allows many knowledge sources to be triggered, or scheduled for execution; the same KS can be triggered multiple times on different data. In the BB1 blackboard system [bb1-manual], a dynamically calculated priority is associated with each triggered KS; the KS with the highest priority is executed first. If a KS makes a clear identification, it can obviate (remove from the schedule) any remaining KS's for the same task. These methods are used to achieve opportunistic control. Bulko [bulko:diss] describes the processing of an example problem in step-by-step detail; the following summarize the control strategies used:
Understanding information from different perceptual modalities about a single situation is an important area of A.I. research. The task of understanding English text and diagrams together is nontrivial but simple enough for useful progress to be made. In addition, a clear test of the validity of the results is available, since the output must be sufficient to allow solving of the physics problem; the output of BEATRIX has been used as input to the physics problem solver of Kook [kook:diss].
Humans find graphical interfaces convenient. Most present graphical interfaces are special-purpose: the graphical primitives that are used, and the ways in which they can be connected and combined, are specialized to the application. The ability to understand diagrams input by the user as free-form drawings would allow the same interface to be used for multiple applications; special-purpose knowledge sources would be needed for particular application areas. With input of line drawings using an optical scanner and computer vision pre-processing, existing drawings (such as blueprints) could be understood without having to be entered by hand.
Drawings alone are not sufficient for complete specification; in many cases, blueprints contain blocks of text as well as drawings. The ability to understand text and drawings together would be needed for successful applications.
It is possible to imagine cases in which the diagram would allow resolution of ambiguity in parsing the English sentences and in which the semantics of the English itself would be insufficient. In the well-known example sentence, ``I saw the man on the hill with the telescope,'' several different parses are possible and correspond to different meanings; a diagram could indicate which meaning was correct. Likewise, the English text might allow resolution of an ambiguity in ``parsing'' the diagram. No cases of either type were found in the examples used in testing BEATRIX. There were many potential ambiguities in matching objects in the diagram and text, but none that would have changed the ``phrase structure'' of either. Nevertheless, this is a possibility, so we identify it as an area for further work. Implementation of the natural language parser within the blackboard framework would make it possible for natural language and diagram parsing to proceed in parallel at the lowest level and to influence each other.
The present system builds only a single interpreta-tion of a problem. A more advanced system should allow representation of alternative interpretations, perhaps like that of [seo-simmons] with certainty factors to indicate the goodness of an interpretation.
Understanding of larger diagrams, such as mechanical drawings or circuit diagrams, is an interesting area for additional research.
[ballard-brown] Ballard, D. H. and Brown, C. M., Computer Vision, Prentice-Hall, 1982.
[bulko:diss] Bulko, W., Understanding Coreference in a System for Solving Physics Word Problems, Ph.D. dissertation, Tech. Report AI-89-102, A.I. Lab, CS Dept., Univ. of Texas at Austin, 1989.
[bulko88] Bulko, W., ``Understanding Text With an Accompanying Diagram'', Proc. First International Conference on Industrial and Engineering Applications of AI and Expert Systems, Tullahoma, TN, 1988, pp. 894-898.
[charniak-mcdermott] Charniak, E. and McDermott, D. V., Introduction to Artificial Intelligence, Addison-Wesley, 1985.
[bb1-manual] Garvey, A., Hewett, M., Schulman, R., and Hayes-Roth, Barbara, ``BB1 User Manual -- Interlisp Verison'', working paper KSL 86-60, Knowledge Systems Lab, Stanford Univ., 1986.
[hanson78] Hanson, A. R. and Riseman, E. M., ``Visions: A Computer System for Interpreting Scenes'', in Hanson and Riseman (eds.), Computer Vision Systems, Academic Press, 1978.
[ksfu74] Fu, K. S., Syntactic Methods in Pattern Recognition, Academic Press, 1974.
[hearsay] Erman, L. D., et al., ``The Hearsay-II Speech-Understanding System: Integrating Knowledge to Resolve Uncertainty'', ACM Computing Surveys, vol 12, no. 2 (June 1980), pp. 213-253.
[kook:diss] Kook, Hyung Joon, A Model-Based Representational Framework for Expert Physics Problem Solving, Ph.D. dissertation, Tech. Report AI-89-103, A.I. Lab, C.S. Dept., Univ. of Texas at Austin, 1989.
[kook-novak] Kook, Hyung Joon and Novak, G., ``Representation of Models for Solving Real-World Physics Problems'', Proc. IEEE Conf. on Applications of A.I., Santa Barbara, CA, March 1990.
[larkin:lmss] Larkin, J., J. McDermott, D. Simon and H. A. Simon. ``Expert and Novice Performance in Solving Physics Problems'', Science, 208 (20 June 1980), pp. 1335-1342.
[nii:hasp] Nii, H. P. et al., ``Signal-to-symbol Transformation: HASP/SIAP Case Study'', A.I. Magazine, vol. 3, no. 2 (Spring 1982), pp. 23-35.
[novak:glisp] Novak, G., ``GLISP: A LISP-Based Programming System With Data Abstraction'', A.I. Magazine, vol. 4, no. 3 (Fall 1983), pp. 37-47.
[novak:isaac] Novak, G., ``Computer Understanding of Physics Problems Stated in Natural Language'', Am. J. Computational Linguistics, Microfiche 53, 1976.
[novak:ijcai] Novak, G., ``Representations of Knowledge in a Program for Solving Physics Problems'', IJCAI, 1977, pp. 286-291.
[seo-simmons] Seo, J. and Simmons, R. F., ``Syntactic Graphs: A Representation for the Union of All Ambiguous Parse Trees'', Tech. Report AI-87-64, A.I. Lab, C.S. Dept., Univ. of Texas at Austin, 1987.
[woods:atn] Woods, W. A., ``Transition Network Grammars for Natural Language Analysis'', Comm. ACM, vol. 13, no. 10 (Oct. 1970), pp. 591-606.