Optimizing Kick: Work Log
11/09/2009
Investigated Austin Villa's old Robocup code. Specificially, I was looking for a good kick to serve as a baseline for the learning algorithm. After locating all of the Lua motion files, I wrote a python parsing script to translate each kick from Lua to Tekkotsu. Kicks were then tested on the Aibo, and the "Power Kick" was selected as a good baseline because it was able to kick the ball up to and beyond the 200cm mark, yet still showed much room for improvement in reliability. I should note that this was essentially the only kick able to get 200cm, so there was not too much choice in the matter.
11/10/2009
Created 6 ball grab postures, each a minor variation on the others. Collected baseline kick accuracy data using grab4.pos follwed by a Power Kick. The collected data can be interpreted using the following diagram:
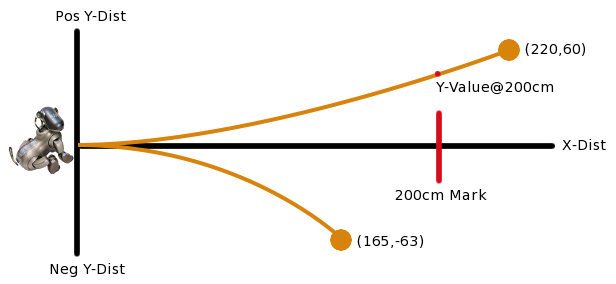 |
All kicks started from the origin and proceeded in the postive X-direction. For each kick several values were recorded. First, the Y-Position@200cm is the positive or negative Y-value when the ball crossed the 200cm mark. If the ball didn't reach the 200cm mark, "na" is given. Additionally, the final resting X and Y positions of the ball are recorded.
| Trial # | Y-Position @200cm | Resting X-Distance(cm) | Resting Y-Distance(cm) |
| 1 | -24 | 382 | -162 |
| 2 | na | 85 | -11 |
| 3 | -3 | 405 | 76 |
| 4 | na | 134 | 84 |
| 5 | 11 | 383 | 91 |
| 6 | na | 139 | -50 |
| 7 | na | 108 | 54 |
| 8 | na | 147 | -13 |
| 9 | 44 | 398 | 104 |
| 10 | 32 | 244 | 71 |
| 11 | 45 | 201 | 45 |
| 12 | 26 | 351 | 91 |
| 13 | na | 166 | 21 |
| 14 | -18 | 244 | 5 |
| 15 | 11 | 248 | 36 |
| 16 | -15 | 202 | -15 |
| 17 | -40 | 281 | -110 |
| 18 | 24 | 206 | 70 |
| 19 | -8 | 204 | 16 |
| 20 | -55 | 200 | -55 |
| 21 | na | 112 | -11 |
| 22 | 16 | 236 | 30 |
| 23 | na | 169 | -44 |
| 24 | 30 | 204 | 32 |
| 25 | 0 | 234 | 35 |
| 26 | -17 | 236 | 1 |
| 27 | na | 84 | 2 |
| 28 | na | 94 | 11 |
| 29 | -49 | 212 | -78 |
| 30 | -17 | 223 | -2 |
| 31 | na | 192 | 37 |
| 32 | -106 | 212 | -125 |
| 33 | na | 164 | -102 |
| 34 | 18 | 245 | 75 |
| 35 | 2 | 250 | 20 |
| 36 | -41 | 217 | -16 |
| 37 | -54 | 239 | -41 |
| 38 | -80 | 225 | -127 |
| 39 | -29 | 240 | -20 |
| 40 | 0 | 224 | 12 |
| 41 | na | 133 | 8 |
| 42 | 1 | 223 | -17 |
| 43 | na | 179 | -11 |
| 44 | na | 121 | 29 |
| 45 | 0 | 279 | -9 |
| 46 | -8 | 217 | 2 |
| 47 | -37 | 250 | -83 |
| 48 | -52 | 204 | -79 |
| 49 | na | 190 | 29 |
| 50 | -4 | 210 | -1 |
From this data the Power Kick can be characterized in several ways:
- Longest Kick: 405cm
- Average X-Displacement: 214.92cm
- Average Y-Displacement: 45.38cm
- Percentage to cross 200cm Mark: 68%
- Percentage Successful Passes: 28%
- Variance in 200cm Y-Displacements: 1157.57*
*Variance was computed only for those passes reaching the 200cm mark.
The following plot shows graphically where each kick came to rest. The start location is the origin, marked here with a red star:
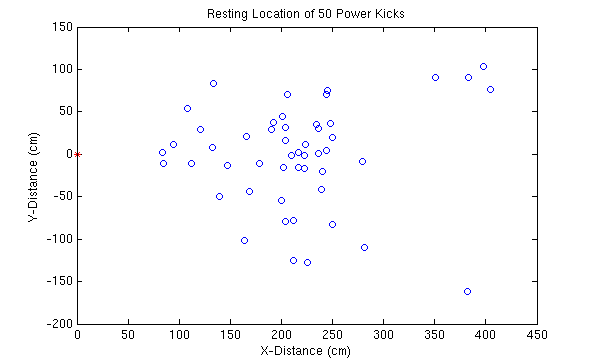
In all respects this seems like a really decent kick. Time will tell whether or not it can be improved.
11/12/2009
Adapted Nate Kohl's Policy Gradient Code to work in the Tekkotsu framework. Acquired a whiteboard left out for recycling which may make a great kicking surface. Also found some things resembling gutters, which would serve as great gutters or pipes to transport the ball.
11/14/2009
Found a wonderful discarded part of a table with a "u" shape. The width of which happens to be nearly exactly that of the Aibo's wingspan. This handy fact allows the Aibo to push against the opposing walls to re-align itself after taking a shot. Also got a simple version of the full system working today. The Aibo will use Policy Gradient to get a kick on the fly, execute the kick, re-align using the walls, and capture the ball when it returns, scoring the kick based on how long the ball took to return.
Right now the bulk of the work left falls into two main jobs: (a) choosing how to parameterize the state space of the kick and (b) constructing the rest of the kicking apparatus.
11/16/2009
Worked with Julian Bishop today to construct the bulk of the distance kicking apparatus. He volunteered to help me in exchange for rights to use the whiteboard after the project is over. All of the boundaries and objects are affixed to the board with industrial strength velcro, allowing them to easily be removed if necessary, leaving a undamaged whiteboard for Julian. Here's the finished product:
 The Aibo sits at the bottom of the brown, wooden "u" shaped contraption and kick upwards.
The Aibo sits at the bottom of the brown, wooden "u" shaped contraption and kick upwards.
 The steel box at the top left corner is used to give variable amounts of incline to the board.
The steel box at the top left corner is used to give variable amounts of incline to the board.
11/17/2009
Today I started the process of learning the kick. To keep things as simple as possible, I decided to attempt to learn kick by varying the raw joint angles. This saved me the work of having to select parameters for the kick. The kick is composed of 6 poses, and each pose consists of 19 joint angles with one additional parameter for the time to remain in that pose. All in all this added up to 114 parameters for each policy. In terms of Policy Gradient's parameters, I decided to use 10 policies per iteration of the algorithm and 1 trial per policy. Ideally the number of policies per iteration should be greater than the number of parameters, and the number of trials per policy should be high enough to get a good estimation of the value of that policy. Ideally, I should be using something like #policies per iteration >= 114 and #trials per policy ~= 10. However, this would take 1140 kicks per iteration which is simply out of the question. Using 10 policies per iteration with 1 trial per policy makes sure iterations end in a decent amount of time.
I was able to perform approximately 500 kicks or 50 iterations over the course of a single battery charge. The resulting logs of policies and scores can be found here: initLearn0.txt, initLearn1.txt.
Overall, the learning stumbled across some very good kicks on occasion but mostly didn't seem to be making smooth progress towards a better kick. Near the end of the battery charge there were quite a few promising kicks in a row. On average, many kicks were quite bad or utter failures. Even worse, I fear that I may have damaged the Aibo through the kicking process. Near the end of the battery charge, I noticed nearly all of the kicks were requesting the Aibo to swing its left front arm's rotator joint backwards, but the actuator didn't have enough torque to complete the request, as this would have required moving the full weight of the Aibo. This would result in the Aibo attempting to actuate the motion but being unable to succeed for a period of some seconds after each kick. It never got so bad that the Aibo shut down as it will typically do when unable to actuate motor commands, but after the duration of the battery, I noticed that the frong left rotator joint was quite stiff. I'm not completely sure that it wasn't stiff before the kicking session, but it seems likely that this was the cause.
In order to remedy this, I have take a couple of precautions. First, immediately after the kick ends, the Aibo is made to go into a neutral pose. This should prevent the actuators from continuing to strain to maintain a badly formulated pose. Second, I will parameterize the kick using symmetry -- all joints on the front and back legs should be made to assume the same value as that of the equivalent joint on the opposite leg. In essence, both back legs should have identical values as should the front. I feel this will both reduce the number of parameters and allow the Aibo to have access to enough torque (using two legs rather than one) to always be able to actuate the given joint commands.
11/18/2009
Changed the parameterization of the task from yesterday's setup. Instead of using all of the raw joint angles as well as timings between postures as parameters, today I tried using a symmetric parameterization. For the each pose, the joints of the front left leg were made to match those of the front right and likewise for the back left and right legs. Still accounting for timings between poses, this reduced the total number of parameters from 114 to 66. I chose to still use 10 policies per iteration which 1 trial per policy.
I learned for the course of one battery charge -- 652 kicks, 65 iterations. I'm pleased to report that the Aibo is still in quite good condition after the duration of this learning session. The two precautions described above and implemented here really seemed to help. Like before, there were occassional good kicks -- one which went off the far end of the board! -- but many bad or mediocre attempts. Overall the algorithm did not seem to converge to any single kicking style although the current kick did evolve through several different phases. The first phase of kicking resembled the original power kick. After that, the kick evolved into a chest hit and ceased to use the head at all. Next, the head was re-introduced but this time in conjunction with the chest -- the Aibo would hit first with the chest and then quickly with the head. Lastly, the kick evolved into only using the head -- similar to the power kick.
The raw kick log can be found here: learn1.txt. The average time for the ball to return from the kick was 2883.76ms. The longest ten kick times were (in ms): 10493, 9397, 6902, 6238, 5981, 5878, 5822, 5822, 5821, 5719. Note that the longest kick was probably made longer by me having to retrieve the ball after it cleared the end of the board.
While it's not clear the Policy Gradient is converging -- or even reliably improving, if nothing else the algorithm has stumbled upon what looks like some really interesting kicks. It may be worthwhile to evaluate some of these kicks in isolation.
In order to determine if the initial policy represents some sort of local maximum, as was the case with attempts to learn starting from the hand coded walk (see Nate Kohl's walk optimization paper), we plot the mean squared difference between the learned policy and the initial policy at each iteration.
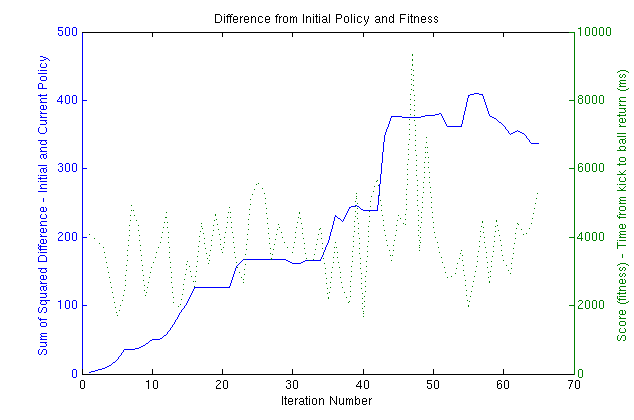
As this plot shows, the algorithm certainly is not stuck in some local maxmimum around the intial policy. As time progresses, the algorithm continues to explore different parts of the parameter space. The fitness, or score, for each iteration is plotted in green. It doesn't seem to show any overall improvement, but is able to keep the overall score pretty consistent. Two python programs, msdParse.py and scoreParse.py were used to parse the mean squared differences and scores from the raw learning logs.
11/21/2009
Today I decided to hill climb on the most promising of the kicks identified from the previous Policy Gradient Run. THe PG code was quite easy to adapt for hill climing -- instead of jumping to a new point in the direction of the gradient every iteration, simply make the new point equal to the best of the policies. My first attempt, which didn't last long due to battery issues, had the disadvantage of re-evaluating the best policy each iteration. While this is not necessarily a bad thing, it seemed like a lot of wasted work to keep on evaluating the same policy again and again. In accordance, I changed the hill climbing algorithm to only evaluate the best policy once, essentially holding its score constant. Other policies were then generated and tested against the best policy's score. After implementing this change, I did another full session of approximately 500 kicks. In this session, each policy was evaulated by 5 trials and there were only two policies per iteration (the current best and the newcomer).
All was going well until I examined the log and noticed that on the second iteration, for some reason, one of the trials had a score of 19.5 seconds. This is obviously incorrect, but it set the average score of the policy to 7.6 seconds, high enough to prevent any other policy from topping it. The next best policies were: 5.3 seconds, which was the initial policy, and 4.9 seconds. The log can be found here: hillClimb1.txt.
The reason for the 19.5 second kick was that the Aibo sometimes pauses and becomes unresponsive to button presses. This happens very rarely, but it's quite a shame that it was only my 2nd iteration out of 104. To resolve this problem, I plan to throw out any scores over approximately 15 seconds and simply repeat the kick. This way, when the Aibo becomes unresponsive, I can simply wait for maybe 30 seconds before pressing the head button again -- without worrying that scores have been skewed.
I decided to give one more go at it today. The previously described 15 second score toss away proved useful 3 times throughout the duration of the run. It also allows me to take a break if needed. I got 89 iterations or approximately 455 kicks out of this charge. Similar to the last, the initial kick proved to be quite strong, only being being bested twice throughout the run. The initial kicked showed an average return of 4.292 seconds, while the best kick, discovered about halfway through the run, had an average of 5.1238 seconds. At this point it really looks like learning has just about maximized and further returns are diminishing. The log can be found here: hillClimb2.txt.
Qualitatively, the best learned kick is looking quite powerful and I look forwards to benchmarking it for comparison against the original "Power Kick".
11/22/2009
Today I benchmarked the best kick from the hill climbing session of yesterday. This would be the kick with average return time of 5.1238 seconds. It's interesting to note that this kick is primarily a chest kick with an occasional bit of head contact. The results of 50 kicks are as follows:
| Trial # | Y-Position @200cm | Resting X-Distance(cm) | Resting Y-Distance(cm) |
| 1 | -40 | 243 | -42 |
| 2 | -24 | 446 | -41 |
| 3 | 7 | 271 | 15 |
| 4 | 41 | 244 | 56 |
| 5 | 16 | 328 | 37 |
| 6 | 92 | 214 | 98 |
| 7 | 6 | 249 | -14 |
| 8 | 0 | 271 | 23 |
| 9 | 36 | 221 | 39 |
| 10 | -36 | 235 | -106 |
| 11 | 52 | 227 | 126 |
| 12 | 13 | 291 | 13 |
| 13 | 45 | 278 | 52 |
| 14 | na | 148 | -25 |
| 15 | 0 | 279 | 20 |
| 16 | 53 | 236 | 73 |
| 17 | na | 173 | -15 |
| 18 | 32 | 311 | 66 |
| 19 | 24 | 238 | 16 |
| 20 | 4 | 226 | -20 |
| 21 | 50 | 210 | 54 |
| 22 | 13 | 319 | 10 |
| 23 | na | 147 | 29 |
| 24 | -21 | 204 | -35 |
| 25 | -16 | 271 | 5 |
| 26 | 9 | 259 | 22 |
| 27 | -13 | 265 | -18 |
| 28 | 24 | 251 | 37 |
| 29 | 23 | 275 | 26 |
| 30 | 15 | 234 | 36 |
| 31 | 43 | 245 | 125 |
| 32 | 34 | 282 | 60 |
| 33 | -19 | 293 | -26 |
| 34 | na | 109 | 81 |
| 35 | 6 | 306 | 20 |
| 36 | -5 | 388 | 40 |
| 37 | -11 | 361 | -11 |
| 38 | 57 | 198 | 58 |
| 39 | -23 | 226 | -67 |
| 40 | 22 | 201 | 22 |
| 41 | 0 | 354 | 24 |
| 42 | 11 | 298 | 30 |
| 43 | -12 | 249 | 8 |
| 44 | na | 182 | 56 |
| 45 | 25 | 287 | 36 |
| 46 | 37 | 217 | 48 |
| 47 | 0 | 442 | 29 |
| 48 | 37 | 272 | 55 |
| 49 | -2 | 327 | -4 |
| 50 | 28 | 293 | 58 |
From this data the Learned Kick can be characterized in several ways:
- Longest Kick: 446cm
- Average X-Displacement: 261.88cm
- Average Y-Displacement: 40.54cm
- Percentage to cross 200cm Mark: 40/50 = 80%
- Percentage Successful Passes: 20/50 = 40%
- Variance in 200cm Y-Displacements: 729.88*
*Variance was computed only for those passes reaching the 200cm mark.
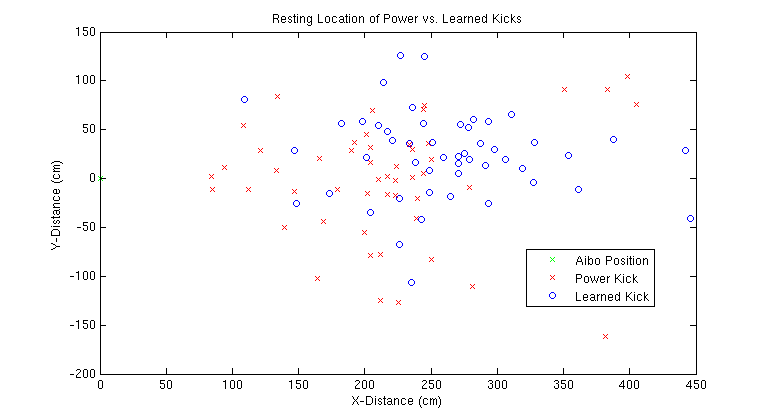
Here is a graph of the resting locations of each of the 50 Learned kicks:
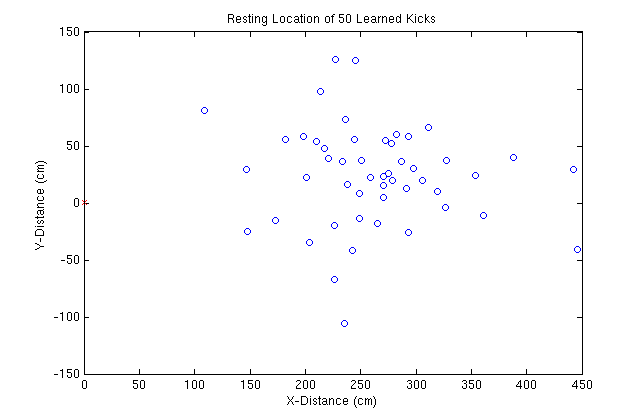
We can now emperically compare the Power Kick to the Learned Kick:
| Metric | Power Kick | Learned Kick | Difference |
| Longest Kick | 405cm | 446cm | 41cm |
| Average X-Distance | 214.92cm | 261.88cm | 46.96cm |
| Average Y-Distance | 45.38cm | 40.54cm | -4.84cm |
| Percentage to Cross 200cm Mark | 68% | 80% | 12% |
| Percentage Successful Passes | 28% | 40% | 12% |
| Variance of 200cm Y-Displacement | 1157.57 | 729.88 | -427.69 |
Overall these improvments look good. The Learned Kicks not only is more powerful, it also is more accurate than the Power Kick. Results of a two-tailed t-test show the distance improvement to be statistically significant with a P-value equal to 0.0013. Resting locations of power kicks and learned kicks are plotted below:
At this point I want to turn my attention towards developing a kick with variable distance. I'm planning on again re-parameterizing the learning -- this time the only parameters will be the timings between switching poses. I'm hoping that by varying the times between poses, the kick will become more or less powerful while still retaining its accuracy. I plan to use Policy Gradient to do the learning and to start with some really high switch times. By keeping track of the results of each kick as PG makes the kicks more powerful, I should have enough data to fit some sort of polynomial to the data points.
11/23/2009
Results are in for the PG on the timings. I used 7 policies per iteration with 4 trials per policy. This gave me 16 complete iterations or just over 448 kicks. The original switch times between poses were set to 50 frames each (400ms each). The weird thing I noticed was that since this is basically a chest/fall/head kick, even with 50 frames per pose, the Aibo still falls on the ball generating a relatively powerful hit. This is a problem because it breaks my assumption that kick power can be modulated simply by changing the timings between poses. I still think this hypothesis is still true, maybe just not for all kicks.
After 16 iterations of PG, we see the timings are reduced from the initial 50 frames, the lowest getting to about 25 frames. These timings are still higher than those of the original kick. Regardless, the power of this slower kick still rivals that of the original. Scores were pretty stable after 16 iterations, so I don't think that the times between frames will ever get down to as low as the original.
I think I need to use a different kick as the base for this learning, one which is more responsive to variations in pose timings.
I have tested the power kick in the same settings as the previous learned kick. I tried two different experiments. First, I attempted to coerce the power kick to kick more gently by setting the score equal to inverse of the time for the ball to return. The initial policy was equal to the original Power Kick timings. The problem was that the learning algorithm found other ways to make the kick less powerfull, in this case by increasing the speed of the motions until the hit was premature. This would have been alright except that it was very unpredictable. Sometimes the hit would be of decent power, othetime it would be quite weak. Stuck at this local optimum, the learning essentially stopped.
Next, I attempted to initialize the policy with very high switch times between frames (75 frame switch times) in this case. As before, PG went some way in lowering the switch times, but found a decent kick (~80% of full power) with much higher switch times. The kick went through two stages: first, when the times were really high, the ball would roll out of the Aibo's arms and be pushed forwards by its feet (not at all the way this kick was intended to work). Second, after some of the switch times were reduced, the kick would hit as intended (with the head). However, after 41 learning iterations, the switch times seem to have stabilized, but they're still approximately twice those used in the original kick. Learned timings were: 78.545, 63.9784, 59.9521, 19.7155, 59.1579, 69.5938 while original timings were: 24, 24, 16, 16, 24, 48. Some of the switch timings actually went up from where they were intialized to! There may be some loose correlations between the magnitudes of the timings, but nothing too concrete.
Now I'm a bit at a loss for how to proceed. I could try to fit a polynomial to the current power kick timings. I could run the same power kick trial again and observe if learning converges at the same spot. I could try and learn only the single timing necessary to hit the ball. I need to do some quick agile investigation and decide on the next coruse of action. If I'm luck I may get another run in tonight. Alternatively I could try to up PG's deltas and re-optimize. This would allow more of the space to be randomly explored with bigger jumps... Less vulnerable to local optima but more unpredictable changes.
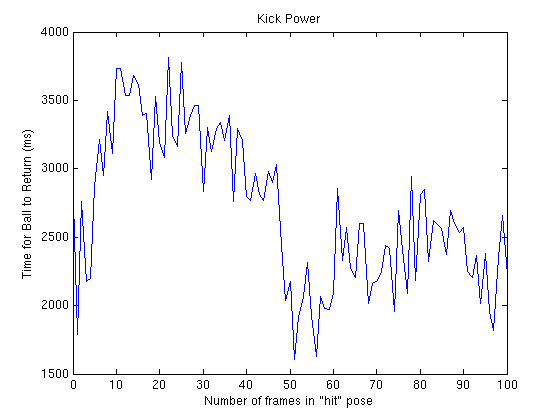
After some investigation I found that in the Power Kick there is a single pose which hits the ball. Varying the timing on this pose seems to vary the power of the overall kick. In order to collect data for model inversion, I varied the timing of this pose from 100 to 0 frames. Each data point was averaged over 3 kicks.
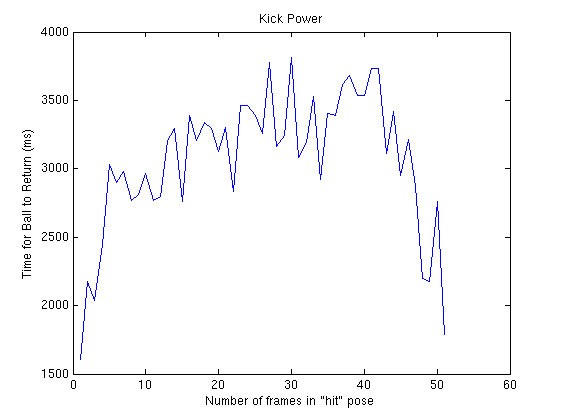
As can be seen from the full run, the results for over 50 frames seem pretty varied. The 50 frame mark is the switch over point where the kick transitions from pushing the ball forwards with the feet (in higher frame numbers) to hitting it with the head (in lower frame numbers). The frame numbers less than 50 have a somewhat regular shape, which I hope to fit a quadratic function to.
I hope to fit a quadratic function to the following graph:
The raw data for these trials can be found here: rampTimeInversion.txt.
11/24/2009
Fitting a quadratic to the kick data, we see the following:
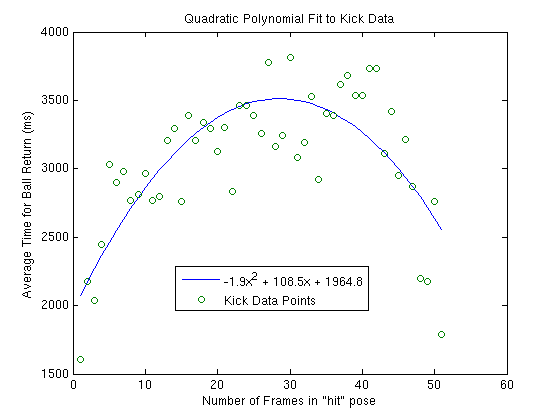
The next thing to do would be to parameterize the kick using the polynomial function. I'm not sure how to evaluate the parameterized kick however. It would be possible to plot the actual distance the ball is kick as a function of the number of frames in the "hit" pose (instead of the average time for the ball to return). This would ground the kick better in human units. I suppose the only real metric by which to evaluate it is whether or not it is useful for making better passes. This would require a lot of further experimentation however.
The following is the graph of actual kick distance as a function of the number of frames. Each data point was an average over the distance of 3 kicks. Here too, a quadratic is fit over the data:
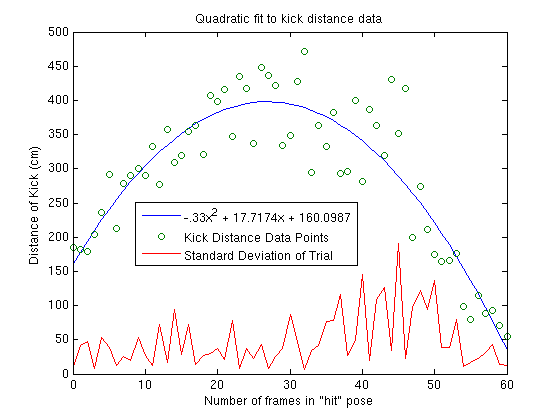
The raw data for these trials can be found here: distInversionData.csv. There are number of things we can gather from this graph. First, the data still looks roughly quadratic. This is a promising thing for the prospect of creating a working parameterized kick. Second, the standard deviations of the 3 kicks in each trial is somewhat larger on the right hand side (higher numbers of hit frames) than on the left. This would imply that all else equal, we would prefer to use the left side of the quadratic function over the right. However, the left side cuts off around 175cm so any desired distance less than that will require using the right side of the quadratic function.
The last and most distressing part of the previous graph is the distance that the power kick is traveling. If you recall, my previous benchmark of the power kick gave it an average kick distance of 214cm, which is obviously getting blown away in this graph (Original Kick used 24 frames in "hit" pose). The reason for this discrepancy is the switch of Aibos. The power kick was originally benchmarked on the first Aibo I was using, which subsequently blew out an actuator. Switching to the second Aibo, we see that the power kick has grown far more powerful. I have not yet re-benchmarked it, but it looks as though it will easily surpass the performance of my learned kick.
Anyway, enough woes. Back to the kick inversion, we can solve the above quadratic equation for x in terms of y. This yields two solutions:
x = (sqrt(15)*sqrt(87437-220*y)+885)/33.
The top corresponds to the left side of the quadratic while the bottom is the right side. With these equations it will be a simple matter to finish the kick inversion.
11/27/2009
The first thing I decided to investigate today was the accuracy of the metric which had been employed throughout previous learning sessions. The assumption was that the power or distance of the kick was correlated with the time it took for the ball to return to the Aibo after being kicked. To test the accuracy of this assumption I setup a second ramp which would feed the ball into the primary ramp, essentially forming a "V" shape. This allowed me to give the ball predictable amounts of velocity depending where on the first ramp it was released from. I discovered that not only was the metric wrong, but more powerful kicks actually took slightly less time to return than less powerful ones! Obviously, I had to redesign the metric. I decided on placing marks as regular 20cm intervals (as shown below). Now, after the Aibo kicks, I note the furthest mark the ball has reached before it returns. This number is then send to the Aibo in the form of a text message. While this is slightly slower for me than simply tapping the Aibo's head to stop a timer, I believe the feedback is informative enough to do some good learning. A picture of the new setup:

In regards the learning, at this point I hope to focus my efforts on proving that learning is effective with regard to an initial policy rather than trying to beat UT's best kick. To this end, I created my own kick which was quite weak (generally mis-hitting or moving the ball only a few cm). I then started using hill climbing to learn from this kick, with 2 trials per policy and 5 policies per iteration. The following is the graph of the score of the best policy at each iteration:
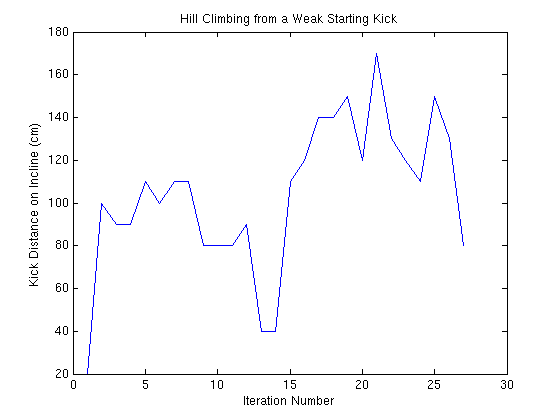
The best kick learned was a really powerful, but unreliable, head kick. The Aibo would essentially slam the head down into the ball, sometimes nearly sending it off the far end of the ramp. Note the max score possible is 200cm on incline, so about 3/4 of the way through the run, the kick was almost at the end of the ramp. I hope this trial, shows that kick learning can certainly be effective, and sometimes quite quick! The log for this run can be found here: noseKickHillClimb.txt.
Next, I used the same hill climbing to continue to optimize my best learned kick (described and benchmarked above). The kick started off kicking somewhere between mark 6 and 7. After about 15 trials, it discovered a slightly more aggressive strain which was putting up consistent 8s. Unfortunately, this good policy had a mis-hit and a bad one took its place about 2/3 of the way through the run. The power on this kick is really quite good now -- and the best part is that it really doesn't use the Aibo's head to hit the ball. This means that it might work equally well on those Aibos with worn out neck joints, the ones for which the power kick is weak. log.
11/28/2009
Today I decided to benchmark the best learned kick against UT's Power Kick using 5 Aibos. Each Aibo performed 5 Power Kicks followed by 5 Learned Kicks. The data can be found here: multiRobotBenchmark.csv. From this data we can see that
| Metric | Power Kick | Learned Kick | Difference |
| Longest Kick | 491cm | 628cm | 137cm |
| Average X-Distance | 290.2cm | 333.56cm | 43.36cm |
| Average Y-Distance | 63.2cm | 78.16cm | 14.96cm |
| Percentage to Cross 200cm Mark | 72% | 100% | 28% |
| Percentage Successful Passes | 36% | 28% | -8% |
| Variance of 200cm Y-Displacement | 501.77 | 877.53 | 357.76 |
From this table we can see that overall the learned kick is on par with the power kick. Some notes of interest. First, the learned kick had the most powerful Aibo kick I've ever seen. It stopped at 628cm after hitting the far wall of the testing room. Thats over 20 feet! Had it been allowed to travel the full course, it may have reached around 650cm. The power kick seems more accurate than the learned kick, but less powerful. This would make sense as the learning process was optimized for increasing power first and accuracy only insofar as the ball lost velocity when colliding one of the ramp's barriers. The main thing which strikes me from this experiment is how variable each of the kicks is on different Aibos. This effect can be seen on the following graph:
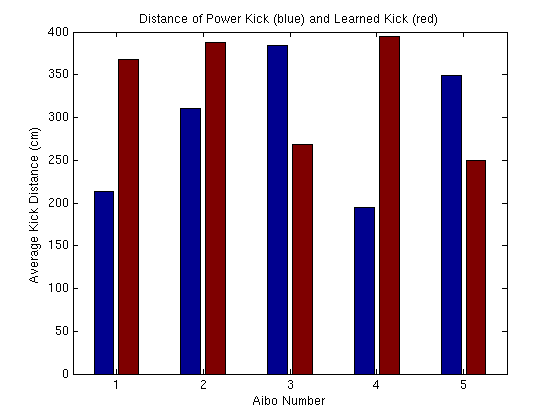
Clearly the decision of which kick is best depends primarily on the Aibo in question. For some Aibos, the Learned Kick overwhelms the Power Kick and vice versa.
To summarize, I feel that learning to optimize kick for distance was indeed successful. Learning from scratch using Hill Climbing resulted in a powerful nose kick after only 25 iterations. Learning from power kick using Policy Gradient didn't converge but did discover several interesting kicks, incuding the best learned kick, which was further optimized with hill climbing. The best learned kick was on par with UT's best kick and was quite different, hitting the ball with the chest rather than the head. In general, the power kick and the learned kick seemed complementary in that the learned kick was strong on those Aibos for which the power kick was weak. Maybe it would be possible for each Aibo to identify its own strongest kick and then use it exclusively.
Learning variable distance kick was also successful. This part of the project was reasonably straightforward -- hopefully it will prove useful for the passing challenge.
At this point I think its past time that I start the writing process. I'm aiming to create a mix of conference paper and research journal -- detailing both the successes and the failures I had throughout the course of the experiment.
12/09/2009
Well the class has wrapped up and the project with it. I was fornuate that my demo went really well. I tried to keep my presentation as short and to the point as possible, knowing that I could easily start rambling about different problems encountered throughout the project. Anyway, I was really fortunate that the learned kick produced quite a powerful kick on the first or second try, nearly reaching the far end of the room. Also, the variable distance kick worked well for all 3 or 4 times it was tested, nearly exactly hitting the correct distance mark.
The project was deemed an overall success and selected as a possible publication in the Robocup symposium. So currently I need change a fair amount of the writing, take some videos, and hopefully establish statistical significance for the experiments.
12/10/2009
There seem to be a few main things needed in terms of experimentation. In terms of timing constraints, I'd like to finish all of the experimentation before going home for break, leaving me with only writing over the break. The list is as follows:
- Picture of each learned kick pose with joints overlayed
- Video of learning process and final results
- Futher experimentation in pursuit of statistical significance
The most important is probably the 3rd item. I will work on this today. I messed up by not recording the mac addresses of the Aibos used for the first part of the final kick benchmark, so it's not an option to simply do more kicks on the same Aibos (as I can't be sure they are actually the same aibos). Instead I will select 5 more Aibos and do kicks on them.
I just finished with this additional kicking experiment. As suggested, 5 Aibos were used with 5 kicks of each type per Aibo. This was exactly the same as when I last did the experiment. The results of the kicks can be found here: multiRobotBenchmark2.csv. Overall, like before, the learned kick was slightly more powerful than the power kick. Interestingly, the mean of both kicks in this set of experiments was higher than that of the last. I think this is a result of overall higher quality Aibos being used for the experiments. The 5 Aibos used in the second experiments were from the Autonomous robots class rather than from the actual Robocup set -- meaning they had been put through less stress and had better joints.
Fortunately while neither of the experiments showed statistically significant improvements in kick distance, the combination of the data from each experiment did show the learned kick to be significantly more powerful than the power kick (p value = 0.0330). The following is the new table:
| Metric | Power Kick | Learned Kick | Difference |
| Longest Kick | 509cm | 628cm | 119cm |
| Average X-Distance | 322.4cm | 373.66cm | 51.26cm |
| Average Y-Distance | 47.4cm | 65.16cm | 17.76cm |
| Percentage to Cross 200cm Mark | 80% | 100% | 20% |
| Percentage Successful Passes | 54% | 48% | -6% |
1/14/2010
Today I collected some experimental data on the variable distance kick. It is meant to serve as an evaluation of the accuracy of this kick. The experimental setup was as follows: 20 random desired kick distances between 60cm and 398cm were generated and the actual kick distances were recorded. varKickEval.csv contains the results of this experiment. To summarize, the variable kick on average was accurate to within 57.8cm of the requested distance.
1/15/2010
I'm currently focusing on replicating my work on variable distance kicking using the learned rather than the power kick. Following the same procedure used to create the variable distance power kick, I recorded kick distances for the learned kick with different number of frames in the "hit" pose. learnedKickDistInversion.csv contains the data recorded from the individual trials. As before, a quadractic was fit to the points:
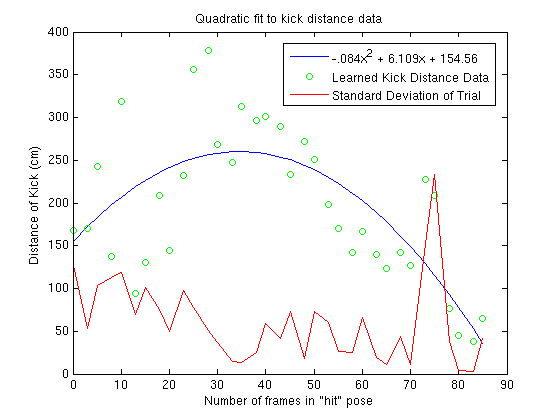
As before, when we solve for y in terms of x, two equations are yielded:
x = (5*sqrt(5)*sqrt(44561-168*y)+1525)/42
These equation correspond to the left and right sides of the quadratic. Next, I evaluated how accurately the learned kick was able to do on the same 20 randomly generated distances that the power kick was benchmarked against yesterday. This data (including yesterday's) can be found in varKickEval2.csv. The learned kick has an average difference of 45.5cm (std. dev. 39.35cm) compared to the power kick's avg. difference of 57.8cm (std. dev. 41.09cm). This difference is not statistically significant but does indicate that the two kicks are reasonably on par with each other in regard to how accurate they are able to place the ball.