NOTE: This transcription was contributed by Martin P.M. van der Burgt, who has devised a process for producing transcripts automatically. Although its markup is incomplete, we believe it serves a useful purpose by virtue of its searchability and its accessibility to text-reading software. It will be replaced by a fully marked-up version when time permits. —HR
A strong P/V-implementation of conditional critical regions.
(This note describes a program of which I announced, before starting on it,
that it would become “ghastly complicated”. I think that my expectation has
been fulfilled. This note is written for various reasons:
1) a successful result of four hours of hard work should be recorded
2) the existence of a program solving the problem in question under
the chosen constraints is, to my knowledge at least, a new discovery
3) I am not certain yet how to describe the program’s development, nor
how to justify the result.)
The problem.
With a semaphore m , initially = 1 , the mutual exclusion problem can be solved by ....P(m); critical section; V(m)..... This, however, introduces the danger of individual starvation in the case of three or more processes, when the P/V-operations are so-ca1led “weakly implemented”. In the weak implementation it is left absolutely undefined which of the blocked processes is allowed to proceed when two or more processes are blocked by P(m) when a V(m) is executed: individual starvation —as the result of “infinite overtaking”— can then not be excluded. It is therefore not unusual to postulate for the P/V-operations a so-called “strong implementation”, in which infinite overtaking is impossible —to admit the processes in the order of “first-come-first-served” would be one way of guaranteeing the strong property— . (Under the assumption of weak P/V-operations we have to prove that for each semaphore s the number of processes blocked by P(s) will, when positive, eventually be reduced to zero. All solutions I know ensure that each semaphore blocks at most one process: under that circumstance the difference between weak and strong implementation disappears. A starvation-free solution using a fixed number of weak semaphores is not known for an unbounded number of processes, and can probably be shown not to exist.)
With conditional critical regions “with r when Bi do Si od” we have exactly the same problem. In a weak implementation of conditional critical regions it is left undefined which of the blocked processes is allowed to continue when after the execution of an Si more than one blocked process has a true guard Bj . Ensuring progress of the individual programs under the assumption of weakly implemented conditional critical regions implies proving that for each blocked process this will eventually become the only blocked process with a true guard; this proof obligation imposes a severe constraint on the programs —several critical regions with the same guard may create serious complications— . For a strong implementation of conditional critical regions —i.e. one that disallows infinite overtaking— it should suffice to prove that infinite blocking of a particular process implies infinite overtaking. More precisely: we have then only to prove that, whenever a process is ready to enter a conditional critical region, the corresponding guard will be true within a finite time. The assumption that this has been proved is denoted by “the assumption of weak absence of starvation on the B-level”. The problem is to give a strong implementation of conditional critical regions for an unbounded number of processes, using a fixed number of (possibly strong) semaphores.
The solution.
Martin Rem has discovered how to implement conditional critical regions
with three semaphores in a very nice way. (Earlier, but somewhat less nice,
this has been done by Coen Bron.) Rem’s solution is a beauty, but it is only
a weak implementation. In this note we shall describe how with two more
semaphores, conditional critical regions can be strongly implemented, by
superimposing upon Hem’s solution the idea of “the binary bakery algorithm”.
Roughly speaking, blocked processes are divided over two groups, L and R ,
and R-processes have priority over L-processes. As long as the R-group
is not empty, it is not allowed to grow; its priority over the L-group and
the assumption of weak absence of starvation on the B-level thus implies
that the R-group gets empty in a finite period of time. Then the L-group
is emptied —either by transferring its members to the R-group or by allowing
them to proceed— before new processes are admitted to the critical
competition.
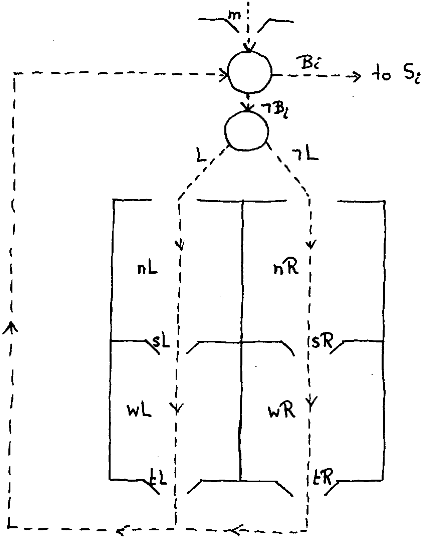
In the above drawing of four rectangular waiting rooms the dotted lines
indicate the possible paths of (mostly blocked) processes. Circles indicate
switches on their paths, each waiting room has an exit marked by the name
—sL, sR, tL, or tR— of a binary semaphore. Inside each waiting room I have
written the name —nL, nR, wL, or wR— of an integer counting the number of
processes inside the corresponding waiting room. When the processes from
the R-group should be allowed to test their guard—i.e. after the execution
of an S— , as in Rem's solution the top-right-hand waiting room is first
emptied into the bottom-right-hand waiting room, before they are admitted
(one at a time) to test their guard. The top-right-hand waiting room has
first to be emptied so that we can collect there the processes from the R-group
of which it has been established that their guards are still false. (For
more details of this part of the algorithm, see EWD629.) At the left-hand
side we have the same arrangement for the processes in the L-group. Then
the critical activity is left (with m = 1) and a new process is admitted
at the top, the bottom waiting rooms are empty and all blocked processes have,
indeed, a false guard.
When m = 1 , the L-group is empty or the R-group is not empty; when the R-group is not empty, L will be true, ensuring that new blocked processes will be placed in the L-group, so that those in the R-group cannot be overtaken by the new ones; when the R-group is empty, the L-group is empty as well and the value of L is immaterial.
When m = 0 and a blocked process tests again its guard, L is false if the process has been admitted to the test via V(tR), thus ensuring that when the process does not escape, it remains in the R-group; L is true when a process has been admitted to the test via V(tL), except when during this critical activity (i.e. period with m = 0 ) the R-group has become empty and the L-group has to be emptied.
This tells us that upon completion of an Si , the boolean L can always be set to false: if the R-group is not empty, its processes will test their guards first, if the R-group has become empty, but the L-group is not, the L-group has to be emptied, and if both are empty, the value of L is immaterial.
The system should be initialized with m = 1 , sL = sR = tL = tR = 0, and nL = nR = wL = wR = 0 ; the initial value of the boolean L is immaterial.
For the following program I am much indebted to W.H.J.Feijen. In my first version the transfer from the members of the L-group to the R-group, when the latter had become empty, bypassed the testing of their guards, and only when the transfer was completed, was testing resumed. Feijen’s first contribution was the remark that it was the purpose of the transfer to empty the L-group, and that therefore no harm was done when during the transfer a blocked proces escaped via its Si if it found its guard true. His second contribution was to urge me to make the picture on the previous page and to draw the paths. As a rule I don’t like such drawings because usually I find them more confusing than helpful. In this case, however, the picture was so helpful that with the picture next to me —and a full awareness of Rem’s
| P(m); | |||||||||
| do non Bi → | |||||||||
| if L → nL:= nL + l; if wL > 0 → V(tL) ▯ wL = 0 → V(m) fi; | |||||||||
| P(sL); nL, wL := nL - l, wL + 1; | |||||||||
| if nL > 0 → V(sL) ▯ nL = 0 → V(tL) fi; | |||||||||
| P(tL); wL:= wL - l | |||||||||
| ▯ non L → nR:= nR + 1; | |||||||||
| if wR > 0 → V(tR) | |||||||||
| ▯ wR = 0 ⇒ L:= true; | |||||||||
| if nL + wL = 0 → V(m) | |||||||||
| ▯ nL > 0 → V(sL) | |||||||||
| ▯ nL = 0 and wL > 0 → V(tL) | |||||||||
| fi; | |||||||||
| P(sR); nR, wR := nR - 1, wR + 1; | |||||||||
| if nR > 0 → V(sR) ▯ nR = 0 → V(tR) fi; | |||||||||
| P(tR); wR:= wR - l | |||||||||
| fi | |||||||||
| od | |||||||||
| Si; | |||||||||
| L:= false; | |||||||||
| if nR + wR > 0 → if nR > 0 → V(sR) ▯ nR = 0 → V(tR) fi | |||||||||
| ▯ nR + wR = 0 → if nL + wL > 0 → if nL > 0 → V(sL) ▯ nL = 0 → V(tL) fi | |||||||||
| ▯ nL + wL = 0 → V(m) | |||||||||
| fi | |||||||||
| fi | |||||||||
Because testing of the guards of the processes in a group always starts with the top waiting room empty, and the critical activity always ends with the bottom waiting rooms empty, for the four semaphores associated with the exits from the waiting rooms a weak implementation suffices. For the semaphore m , however, we need a strong implementation.
In a sense the whole experiment was a disappointment. Our original goal was an implementation of the conditional critical regions that would be strong by virtue of the strength of the sequencing primitives used. We have not been able to reach that goal, as we have only been able to ensure the strength by means of the “binary bakery algorithm”, as reflected in the L-group and the R-group. Whether this goal can be reached at all is unknown; on account of yesterday’s experience I doubt.
Finally: although it is conceptually very satisfying that this scheduling problem can be solved with a fixed number of semaphores, I can hardly say that I like the program. As the program stands it is rather an incentive to search for more appropriate means.
| Plataanstraat 5 | prof.dr.Edsger W.Dijkstra |
| 5671 AL Nuenen | Burroughs Research Fellow |
| The Netherlands |
Transcribed by Martin P.M. van der Burgt
Last revision