Partitioning the edges of the complete graphs into trees or cycles.

by the Tuesday Afternoon Club

The k(2k-1) edges of the complete 2k-graph can be partitioned into k subspanning trees. We demonstrate the construction for 2k=8:

EWD741 figure 1 the three remaining trees are obtained by successive rotations over π/4.

The k(2k+1) edges of the complete (2k+1)-graph can be partitioned into k subspanning cycles. We demonstrate the construction for 2k+1=9:

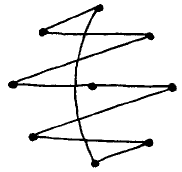EWD741 figure 2 the three remaining cycles are obtained by successive rotations over π/4.


Plataanstraat 5
5671 AL NUENEN
The Netherlands 		27 May 1980
prof. dr. Edsger W.Dijkstra
Burroughs Research Fellow