My mother’s proof of the Butterfly Theorem (see EWD866)
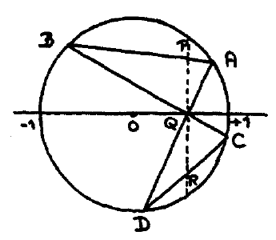
In a circle with centre O the chords AD and BC intersect one another in Q. The line PQR intersects AB in P and CD in R and is orthogonal to OQ. Prove PQ = QR.
(The name “Butterfly Theorem” is derived from the shape of the quadrilateral ABCD.)
Mother only used that the circle is a conic section and that Q divides the dotted chord into two equal halves. With O in the origin and the dotted chord of length 2⋅q along the y-axis, the substitution x ≔ 0 reduces the equation of the conic section to
y2 = q2 (0)
The substitution x ≔ 0 reduces the equation of the (degenerate) conic section consisting of the lines AD and BC to
y2 = 0 (1)
The substitution x ≔ 0 reduces the equation of any other member of the bundle on those two, i.e. of any other conic section through A, B, C, and D, to
y2 + λ ⋅ y2 = q2 + λ ⋅ O or
(1 + λ) ⋅ y2 = q2 (2)
for some λ. This holds in particular for the (degenerate) conic section consisting of the lines AB and CD. Since the two roots of (2) have equal absolute values, this concludes the proof.
* *
*
Mother’s proof is far superior to mine. I worked with line bundles. By recognizing pairs of lines as conic sections she did it with a bundle of conic sections. And, in passing, she generalized the theorem. To quote Ross Honsberger “Bless her heart!”.
|
Plataanstraat 5 5671 AL NUENEN The Netherlands |
18 December 1983 prof.dr.Edsger W. Dijkstra Burroughs Research Fellow |