E.W.Dijkstra Archive: A monotonicity argument revisited (EWD 1014)

(This is derived from AvG36/EWD878 d.d. 22 Feb. 1984.)

Square brackets denote universal quantification over x and y. Function f satisfies

[ x < y ⇒ f.x.y < f.y.x ] (0)

We observe (0) =p < q ≡ q > p [ y > x ⇒ f.y.x > f.x.y ] =change dummies x,y := y,x [ x > y ⇒ f.x.y > f.y.x ] ⇒pair-wise disjunction with (0); p < q ∨ p > q ≡ p ≠ q [ x ≠ y ⇒ f.x.y ≠ f.y.x ] =contrapositive [ x = y ⇐ f.x.y = f.y.x ] =Leibniz: [x = y ⇒ f.x.y = f.y.x] [ x = y ≡ f.x.y = f.y.x ](1)

^* _* ^*

Consider the triangle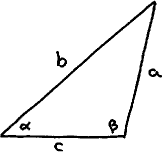
The triangle labeled angles: alpha, bravo and sides a, b, c.

We were taught two theorems
"The sides opposite to equal angles are equal" or

α = β ⇒ a = b (2)

"The angles opposite to equal sides are equal" or

α = β ⇐ a = b (3)

The theorems were proved separately; both were geometrical proofs using congruent triangles. Prior to that it had already been shown that opposite to the larger angle lies the larger side, i.e.

[ α < β ⇒ a < b ] . (4)

Consider now, for fixed c, a, and b functions of α and β. For reasons of symmetry a is the same function of (α, β) as b is of (β, α). i.e. for some f we have

a = f.α.β and b = f.β.α

Substituting this in (4) we see that this f satisfies (0), hence, on account of (1) we immediately get, as logical consequence

[ α = β ≡ a = b ] .

i.e. the conjunction of (2) and (3): the geometrical proofs with the congruent triangles are superfluous. The proofs were an obfuscation.

A similar pair of theorems is

"An isosceles triangle has two angle bisectors of equal length" and
"A triangle with two angle bisectors of equal length is isosceles"

The one is considered easy to prove, the other one difficult. Thanks to the above, both theorems are subsumed in "The larger angle has the shorter bisector.", which follows from the formula for the length of the bisector of α:

√
b∙c∙(1 − (
a
b+c
)²)

which is a decreasing function of a and an increasing function of b.

The above suggests that, in the way in which geometry is taught, logic is underexploited. Historically understandable, but regrettable all the same.