On the Economy of doing Mathematics
(Written for the 2nd International Conference on the Mathematics of Program Construction, 29th June – 3rd July, 1992, Oxford).
Every honest scientist regularly does some soul searching; he then tries to analyse how well he is doing and if his progress is still towards his original goal. Three years ago, at the previous conference on the Mathematics of Program Construction, I observed some of such soul searching among the scientists there present, and I observed more doubt than faith. The first part of this talk is therefore devoted to my explanation of why I think most of those doubts unjustified.
One general remark about an unexpected similarity between the programming community and the mathematical community first. In the past, art and science of programming have seriously suffered from the concept of “the average programmer” and the widespread feeling that his (severe) intellectual limitations should be respected. Industrial pressure and propaganda promoted the view that, with the proper programming language, programming did not post a major challenge and did not require mental gifts or education, thus creating an atmosphere in which self-censorship witheld many a scientist from exploring the more serious forms of programming methodology. I would like to point out that, in very much the same way, mathematics has suffered and still suffers from the tyranny of “the average mathematician”. Improvements in notation, in language or concepts are rejected because such deviations from the hallowed tradition would only confuse the average mathematician, and today’s mathematical educators who think that they are doing something great by turning a piece of mathematics into a video game are as misguided as earlier recruiters for the programming profession. The similarity is striking, the only difference between the average programming and the average mathematician possibly being that the latter tends to believe that he is brighter than everybody else. And this concludes my general introductory remark.
* *
*
Let us now have a look at various supposed reasons for losing faith in mathematical construction of programs.
• “Formal program derivation is no good because industry rejects it.” Well, what else do you expect? For four decades, the computing industry has been guided by businessmen, bean-counters, and an occasional electronic engineer. They have carefully seen to it that computing science had no influence whatsoever on their product line, and, now the computer industry is in problems, computing science gets the blame. (Ironically, many CS departments now feel “guilty” and obliged to turn out more “practical” graduates, i.e. people with the attitudes that got the computer industry into trouble in the first place.) Having put the blame on our doorstep, they have “justified” rejecting our work, and they have to continue to do so, so as to save their own image.
In short: when industry rejects formal methods, it is not because formal methods are no good, but because industry is no better.
• “Formal methods are no good because the practitioner rejects them.” This may sound convincing to you, but only if you don’t know the practitioners. My eyes were opened more than 20 years ago on a lecturing trip to Paris with, on the way back, a performance in Brussels. It was the first time I showed to foreign audiences how to write programs that were intended to be correct by construction. In Paris, my talk was very well-received, half the audience getting about as excited as I was; in Brussels, however, the talk fell flat on its face: it was a complete flop. I was addressing the people at a large software house, and in my innocence I had expected them to be interested in a way of designing programs such that one could keep them firmly under one’s intellectual control. The management of the company, which derived its financial stability from its maintenance contracts, felt the design of flawless software not to be in the company’s interest, so they rejected my recommendations for sound commercial reasons. The programmers, to my surprise, rejected them too: for them, programming was tedious, but debugging was fun! It turned out that they derived the major part of their professional excitement from not quite understanding what they were doing and from chasing the bugs that should not have been introduced in the first place.
In short: formal techniques are rejected by those practitioners that are hackers instead of professionals.
• “Formal methods are no good because quote a few colleagues in your own CS department are opposed to them.” This sounds like a much more serious objection, but fades away as soon as you know the reasons why your colleague objects. The one main reason is that, deep in his heart, your colleague is a hacker, that by advocating formal techniques you are promoting quality standards he cannot meet, and that consequently, he feels discriminated against. Such a colleague should be pitied instead of taken seriously. The other main reason is political. Once growth of the Department has been accepted as the target, one can no longer afford to present Computing as a serious Science, the mastery of which is sufficiently demanding to scare away the average student. Such a political colleague has adopted the morals of the bestseller society, and should be despised instead of taken seriously.
• “Formal methods are no good, for even mathematicians have not accepted them.” This sounds really serious, for mathematics embodies an intellectual tradition of thousands of years. Closer inspection shows that that is precisely one of its problems. While the Renaissance sent all of classical “science” to the rubbish heap, much of classical mathematics was accepted as the standard. This is one of the explanations of the fact that, to this very day, the Mathematical Guild is much more medieval than, say, the Physical Guild, and that informality — not to say, handwaving — is the hallmark of the Mathematical Guild Member: frantically trying to distinguish between form and contents, he neglects the form and thus obscures the contents. Never having given formal techniques, i.e. the manipulation of uninterpreted formulae, a fair chance, he does not have the right to say that they are no good.
This may be the place to point out that most programmers and most mathematicians work in linguistically comparable situations. The programmer uses symbols of a “programming language”, the mathematician uses symbols of a “reasoning language”. For the sake of compatibility, both languages are accepted as de-facto standards although both are bad, and totally defective as carriers of a formal system. These people do, indeed work in an environment in which formal techniques are hard to apply directly, but this is the consequence of well-identified shortcomings of the “languages” they have accepted as standards.
* *
*
Suddenly having to run a children’s party for kids ranging from 8 to 13 years of age, I gave them pencil and paper and asked them the well-known question whether it is possible to cover with 31 2x1 dominoes the 8x8 square from which 2 unit squares at opposite corners have been removed. They all tried doing it and failed each time. After about 20 minutes, the consensus was that it could not be done, but they agreed that impossibility could not be concluded from a sample of failed efforts. They also agreed that neither the party nor their patience would suffice for an exhaustive test, and their attention was on the verge of turning to something else when I showed to them how the impossibility can be established by means of the well-known counting argument inspired by the coloring of the chessboard. You should have seen the excitement on those young faces! They were absolutely fascinated, and rightly so, for even in this very simple setting they had caught a glimpse of the unequalled power of mathematics.
In connection with this problem I would like to point out two things. Firstly, it is not just brute force versus reasoning, for even the exhaustive “experiment” requires an argument that no cases have been overlooked. In other words, the two approaches represent two extremes on a spectrum of arguments: a very clumsy one and a very effective one. Secondly, the problem has effortlessly been generalized to many other sizes than 8x8. The importance of these observations is that mathematics emerges as something very different from what the Oxford Dictionaries give you, viz. “the abstract science of space, number, and quantity”; mathematics rather emerges as “the art and science of effective reasoning”, regardless of what the reasoning is supposed to be about. The traditional mathematician recognizes and appreciates mathematical elegance when he sees it. I propose to go one step further, and to consider elegance an essential ingredient of mathematics: if it is clumsy, it is not mathematics.
For the improvement of the efficiency of the reasoning process, three main devices have been found effective:
(i) adopting a notation that captures what is essential and nothing more (among other things to enable what A.J.M. van Gasteren has called “disentanglement”)
(ii) restricting reasoning steps to a well-defined (and modest) repertoire of manipulations
(iii) adopting a notation that yields formulae that are well-geared to our manipulative needs
Remark Alfred North Whitehead almost understood this; he was, however, willing to sacrifice ease of manipulation to brevity. A small study of the ergonomics of formula writing shows that the stress on his kind of brevity was misguided. (End of Remark.)
All these devices are closely connected to notation, and it is worth pointing out that the typical mathematician is very ambivalent about the importance of notation: on the one hand he knows that a good notation can make the difference between day and night, on the other hand he considers explicit attention paid to notation wasted. Quite typical was the reaction of a rather pure mathematician that had attended several days of lectures that W.H.J. Feijen and I gave in the second half of the 70s: he was very impressed by the power of our formal apparatus but regretted our deviations from standard notational conventions, not realizing that these deviations had been a conditio sine qua non. The probable explanation of the mathematical ambivalence towards notation is that the average mathematician is still a Platonist, for whom formulae primarily have a descriptive rôle, and are not meant for uninterpreted manipulation, “in their own right” so to speak; moreover, his unfamiliarity with formal grammars makes many notational issues impossible for him to discuss.
But let me give you three tiny examples of the importance of notation.
(i) Among a large number of electronic engineers I have established that, while all are certain that “and” distributes over “or”, a significant majority is ignorant of, or very uncomfortable with, the inverse distribution. This shocking observation has a simple explanation: in their crummy notation, the familiar distribution is rendered by the familiar x(y + z) = xy + xz , the unfamiliar distribution is rendered by the unfamiliar x + yz = (x+y)(x+z) .
(ii) With ∑ , π , ∀ , ∃ , ↑ or ↓ for the quantifier Q, the “1-point rule” is
⟨ Qi : i = n : t.i ⟩ = t.n
For ∑ and π , mathematicians know it, probably in the forms
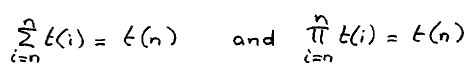
For ∀ and ∃ , they do not know the 1-point rule, working, as they do, in these cases without “range” for the dummy; they would have to code them as something like
(∀i (i = n ⇒ t(i)) = t(n) and
(∃i (i = n ⋀ t(i)) = t(n) ,
forms sufficiently opaque to make these formulae unknown. (And not knowing these 1-point rules really hurts, as they are the main devices for equating a quantified expression to an expression without quantifier.)
(iii) As a final example: recently I saw for a nonassociative relation between predicates an infix operator, say M, being introduced. An important property of M was rendered by
[ ⟨∀i ∷ p.i M q.i⟩ ⇒ (⟨∀i ∷ p.i⟩ M ⟨∀i ∷ q.i⟩) ]
Had we written M.(x,y) for x M y , we could have used that quantification distributes over pair-forming, i.e.
[ ⟨∀i ∷ (p.i , q.i)⟩ ≡ (⟨∀i ∷ p.i⟩ , ⟨∀i ∷ q.i⟩) ]
and with the dummy w of type “predicate pair”, the above property of M could have been written
[ ⟨∀w ∷ M.w⟩ ⇒ M.⟨∀w ∷ w⟩ ]
an implication familiar from conjunctivity. But it is hard to exploit the fact that quantification distributes over pair-forming if the pair has been pulled apart by an infix operator.
The ambivalence towards notation is reflected in what I am tempted to call “hybrid theories”; these are very traditional and are warmly recommended to this very day. The designer of a hybrid theory has the feeling of creating two things: firstly, the subject matter of the theory, and, secondly, a “language” to discuss the subject matter in. Besides metaphors, jargon and definitions, “language” includes here formalisms as well.
The idea behind the hybrid theories is that arguments and calculations, by definition formulated in the new language, are to be understood, interpreted, and given “meaning” in terms of the new subject matter. Usually the language is a semi-formal system, in which many steps of the argument are “justified” by an appeal to our intuition about the subject matter.
By giving enough care to the design of the language, by making it sufficiently elaborate and unambiguous, the validity of conclusions about the subject matter becomes a linguistics characteristic of the sentences describing the argument. In the ultimate case, reasoning about and in terms of the subject matter is replaced by the manipulation of uninterpreted formulae, by calculations in which the original subject matter has disappeared from the picture. The theory is now no longer hybrid, and according to your taste you may say that theory design has been degraded to or simplified to a linguistical exercise.
I have observed that even in the presence of a simple and effective formalism, mathematicians of a more conservative persuasion are opposed to such calculational manipulation of formulae and advocate their constant interpretation in terms of the constituents of the intended model. They defend this interpretation, also called “appeal to intuition” mainly on two grounds. Their first argument is that the close ties to the intended model serve as a source of inspiration as to what to conjecture and how to prove it. I have my doubts about this but I don’t need to elaborate on those because the sudden focus on “the source of inspiration” reveals a lack of separation of concerns: because there is a job to be done we are interested in the structure of the arguments and not in the psychological habits and mental addictions of individual mathematicians. Their second argument for constant interpretation is that it is an effective protection against the erroneous derivation of what, when interpreted, is obvious nonsense: in short, constant interpretation for safety’s sake. It is my contention that the second argument reflects a most harmful mistake, from which we should recover as quickly as possible: adhering to it is ineffective, paralyzing, misleading, and expensive.
• It is ineffective in the sense that it only protects us against those erroneous conclusions for which the model used readily provides an obvious counterexample. It is of the same level as trying to base confidence in the correctness of a program on testing it.
• It is paralyzing. You see, a calculus really helps us by freeing us from the fetters of our minds, by the eminently feasible manipulation of formulae whose interpretation in terms of a model completely defies our powers of imagination. Insistence on constant interpretation would rule out the most effective use of the calculus.
• It is misleading because the model is always overspecific and constant interpretation invites the introduction of steps that are only valid for the model the author has at that moment in mind, but are not valid in general. It is this hybrid reasoning that has given all sorts of theorems a very fuzzy range of validity. People working with automatic theorem provers discovered that in geometry most theorems are wrong in the sense that “the obvious exceptions” are not mentioned in the theorem statements; more alarming is that those exceptions don’t surface in the published proofs either.
• It is expensive because the constant “translocation from formulae to interpretation is a considerable burden. (In order to reduce this burden, P. Halmos strongly recommends to avoid formula with quantifiers!)
The moral is clear: for doing high-quality mathematics effectively, verbal and pictorial reasoning have to be replaced by calculational reasoning: logic’s rôle is no longer to mimic human reasoning, but to provide a calculational alternative. We have no choice, and, as a result, we are entitled to view the design of a mathematical theory as a linguistic exercise, and to rate linguistical simplifications as methodological improvements.
A major such improvement is the restriction to unambiguous formulae. It is easily implemented and is a great simplification compared to the unwritten rules of disambiguation that are invoked by “but everyone understands what is meant”. I remember how I was ridiculed by my colleagues, and accused of mannerism and arrogance, just because I avoided a few traditional ambiguities, but that was a quarter of a century ago and by now the mathematical community could be wiser.
A next step is to recognize that it is not string or symbol manipulation that we are doing, but formula manipulation; we replace not just substrings but subexpressions, and formula manipulation is therefore simplified by easing the parsing. Context-dependent grammars, for instance, are not recommended. I remember a text in which x = y ⋀ z had to be parsed as x = (y ⋀ z) for boolean x,y but as (x = y) ⋀ z otherwise, and such a convention is definitely misleading. These are not minor details that can be ignored. (The only calculational errors I am aware of having made in the last decade were caused by parsing errors.)
I would now like to draw your attention briefly to a linguistic simplification of a somewhat different nature, which took place in an area familiar to all of us, viz. program semantics. In this area, the 60s closed after the pioneering work of Naur and Floyd with Hoare’s Axiomatic Basis, where the rules of the game were couched as “inference rules”, expressed in their own formalism. A main reason for publishing in the 70s the predicate transformer semantics was that the latter eliminated the whole concept of inference rules by subsuming them in the boolean algebra of predicates, which was needed anyhow. The paper was written under the assumption that this simplification would be noticed without being pointed out; in retrospect I think that that assumption was a mistake.
Let me now turn to what might turn out to be the most significant simplification that is taking place these decades. If it is as significant as I estimate, it will need a name; my provisional name, description but a bit long is “domain removal”. Let me illustrate it with a very simple but striking example.
Let us consider the transitive relation ∝ (“fish”) i.e. for all p,q,r
p ∝ q ⋀ q ∝ r ⇒ p ∝ r ,
and the two ways of correcting the erroneous conclusion that p ∝ r holds for any p,r . The erroneous argument is “choose a q such that p ∝ q and q ∝ r both hold; p ∝ r then follows from transitivity”. The obvious error is that such a q need not exist, i.e. we can only demonstrate
⟨∃q ∷ p ∝ q ⋀ q ∝ r ⟩ ⇒ p ∝ r
The traditional argument goes as follows. Assume the antecedent ⟨∃q ∷ p ∝ q ⋀ q ∝ r ⟩ ; this means that we can choose a value that we shall call k such that p ∝ k ⋀ k ∝ r ; and now we can conclude p ∝ r on account of the transitivity of ∝ .
The alternative argument can be rendered by:
We observe for any p,r
⟨∃q ∷ p ∝ q ⋀ q ∝ r ⟩ ⇒ p ∝ r
= {predicate calculus}
⟨∀q ∷ p ∝ q ⋀ q ∝ r ⇒ p ∝ r ⟩
= {∝ is transitive}
true
These two arguments illustrate the difference in vitro, so to speak. In the traditional argument, identifiers are used to name variables of the appropriate type, identifier k, however, names a value of that type. In the alternative argument, the identifiers all name variables, and, consequently, the possible values of the variables have disappeared from the picture. By not mentioning the values, their domain has been removed. In demonstrating an existential quantification by constructing a witness and, conversely, in using an existential quantification by naming a witness, Gentzen’s Natural Deduction advocates proofs of the needlessly complicated structure.
Whether identifiers are names of variables or (unique!) names of values turns out to be a traditional unclarity. “Consider points A, B, C and D in the real Eucliden plane, etc.”: it is now unclear whether coincidence is excluded or not.
Proofs of uniqueness traditionally suffer from this complication. It means that for some given P one has to show
P.x ⋀ P.y ⇒ x = y for all x,y
Authors that are unclear about the status of their identifiers are uncomfortable about this because, with x and y unique names of values, x ≠ y holds by definition. They feel obliged to embed the above, packaging it as a reductio ad adsurdum:
“Let P.x; assume that there is another value y such that P.y . But P.x ⋀ P.y implies x = y, which is a contradiction, hence no such y exists.”
Another complication is that value-naming easily induces case analysis. Some time ago the problem of the finite number of couples circulated. You had to show that in each couple husband and wife were of the same age if
(i) the oldests of either sex had the same age, and
(ii) if two couples did a wife swap, the minimum age in the two new combinations were equal to each other.
The traditional argument is in two steps. It first establishes on account of (i) and (ii) the existence of a couple of which both husband and wife are of maximum age. In the second step it establishes that then and on account of (ii) in any other couple husband and wife are of the same age. When formulating this carefully, taking into account that there need not exist a second couple and that more than one man and one woman may enjoy the maximum age, I could not avoid all sorts of case distinctions. The trouble with this argument is, of course, that it has to refer to a specific couple. Here is, in contrast, the calculation in which no specific husband, wife, age or couple is named; the variables x,y are of type “couple”. We are given
(i) ⟨↑y ∷ m.y⟩ = ⟨↑y ∷ f.y⟩
(ii) ⟨∀x,y ∷ m.x ↓ f.y = f.x ↓ m.y⟩
and observe for any x
m.x = f.x
= {calculus: law of absorption}
m.x ↓ ⟨↑y ∷ m.y⟩ = f.x ↓ ⟨↑y ∷ f.y⟩
= {(i)}
m.x ↓ ⟨↑y ∷ f.y⟩ = f.x ↓ ⟨↑y ∷ m.y⟩
= {↑↓calculus: ↓ distributes over ↑}
⟨↑y ∷ m.x ↓ f.y⟩ = ⟨↑y ∷ f.x ↓ m.y⟩
= {(ii)}
true
which concludes the proof without any case analysis. (Some of the simplification is due to the fact that the range in (ii) includes x=y, the rest of the simplification is due to the fact that the calculation names no specific couple, only variables of type “couple”.)
The fact that, in useful calculation like the above, the possible values of the variables are totally irrelevant and can therefore profitably be ignored has been seen and explained in 1840 by D. F. Gregory — in “On the Real Nature of Symbolic Algebra” [Trans. Roy. Soc. Edinburgh 14, (1840), 208-216] — :
“The light, then, in which I would consider symbolic algebra, is, that it is the science which treates of the combination of operations defined not by their nature, that is by what they are or what they do, but by the laws of combination to which they are subject.”
Gregory knew that the domain of values could be ignored. So did John D. Lipson, in whose book “Elements of Algebra and Algebraic Computing” I found the above quotation. The amazing thing is that all texts about algebra I saw, Lipson’s book included, introduce algebras as defined on a (named) set of values! Gregory’s insight seems uniformly ignored. Sad.
All this has a direct parallel in programming. In order to establish the correctness of a program one can try a number of test cases, but for all other applications of the program one has to rely on an argument as to why they are correct. The purpose of the argument is to reduce the number of test cases needed, and I would like you to appreciate the dramatic change that occurs when the number of test cases needed is reduced to zero. Suddenly we don’t need a machine anymore, because we are no longer interested in computations. That is, we are no longer interested in individual machine states (because that is what computations are about). Reasoning about programs then becomes reasoning about subsets of machine states as characterized by their characteristic predicates, e.g.
{s | X.s}
The next step — known as “lifting” — is to rewrite relations between predicates, e.g. rewrite
⟨∀s: s ∈ S: X.s ≡ Y.s ⋀ Z.s⟩
as
[X ≡ Y ⋀ S]
because the most effective way of eliminating machine states from our considerations is by removal of the last variable that ranges over them. From variables of type “machine state” — like “s” — we have gone to variables of type “predicate” — like “X, Y, and Z” —. I cannot stress enough the economy of not having to deal with both types of variables. In other words, besides being ineffective, quality control of programs by means of testing is conceptually expensive.
The characteristic functions of singletons are called “point predicates”. My great surprise over the last ten years is the power of what became known as “pointless logic”, i.e. predicate calculus without the axiom that postulates the existence of point predicates. The calculus is extremely elegant: it is like a purified set theory, for which traditional sets composed of elements are an overspecific model. It is extremely powerful. It admits extension to “pointless relational calculus” which for me had many surprises in store. For notions like transitivity and well-foundedness I grew up with definitions in terms of individual elements, but the use of those elements is an obfuscation, for the concepts can be beautifully embedded in pointless relational calculus. Of all I have seen, it is the ultimate of removal of the inessential.
Finally, let me add to these pleasant surprises a pleasant observation: the average calculational proof is very short. I can truly do no better than relay to you the valuable advice my dear mother gave me almost half a century ago: “And, remember, when you need more than five lines, you are probably on the wrong track.”.