On some very binary patterns
In his last manuscript “A collection of nice problems”, Jan L.A. van de Snepscheut described the following one-person game. There is a table with four coins in the positions north, east, south and west, and the player’s goal is to get them all in the same orientation, i.e. all heads or all tails. The player never sees the coins but will be informed as soon as he has reached his goal. A move consists of the player mentioning one or more positions in which the coins will then be turned over; the complication is that, prior to each move, the table is rotated by a multiple of 90°; the multiple remains unknown to the player and may vary from move to move.
The version of the problem that Rutger M. Dijkstra told me after the 3rd International Conference on the Mathematics of Program Construction at Kloster Irsee, Germany — where it had apparently circulated — had been sanitized in that the player’s goal had been simplified to “all coins in a given orientation, say heads”. Moreover, Rutger had generalized the number of coins from 4 to any power of 2, a generalization that was extremely helpful because it was an irresistible invitation to look for a nicely recursive solution.
There are three reasons for writing this note. Firstly, when I had designed a winning strategy, I did not know how to present it nicely. Secondly, my solution’s correctness implied a theorem (of sorts) that I did not yet know how to formulate decently. Finally, there is my hope that Frans E.J. Kruseman Aretz, to whom this note is dedicated, will appreciate my efforts.
* *
*
In order to avoid all ambiguity, let us formulate the game as a program of which termination has to be guaranteed.
We introduce the type BV of bit vectors of length n (n ≥ 1 ; in Jan’s original problem, n = 4), and two constants ZEROS and ONES of type BV (viz. the sequence of n 0s and the sequence of n 1s respectively). On arguments of type BV, we denote the bit-wise addition modulo 2 (also known as “the carry-less sum”) by an infix ∔ ; as any sum, it is symmetric and associative. Finally, we introduce a function
rot: int → (BV → BV)
of which we know that rot.i.bv is some rotation of bv. We have no further knowledge how rot.i depends on i (which will act below as move number).
In the following program block, the state of the table with its coins is represented by an initialized global variable
t: BV
The player’s strategy is represented by a global function
ps: int → BV ,
where the 1s in the bit vector ps.i identify the positions in which the coins are turned over in the i-th move.
In the original problem we were interested in the termination of
(0) |[ var i: int; i ≔ 1
; do t ≠ ZEROS ⋀ t ≠ ONES →
t ≔ rot.i.t ∔ ps.i ; i ≔ i + 1
od
]|
but in the rest of this note we deal with the “sanitized” version
(1) |[ var i: int; i ≔ 1
; do t ≠ ZEROS →
t ≔ rot.i.t ∔ ps.i ; i ≔ i + 1
od
]|
Remark Note that in simplifying the guard we have weakened it. Hence, termination of the sanitized version (1) implies termination of the original program (0). (End of Remark.)
The challenge now is to design such a function ps that (1) terminates independently of the initial value of t and independently of how rot.i depends on i.
The purpose of our next massaging is to facilitate keeping track of the identity of the coins so as to ease tracing the influence of a change in the initial value of t.
We observe that as far as the identity of the coins turned over in a move is concerned, the effect of how far the table has been turned clockwise can also be obtained by the corresponding anti-clockwise turn of the player’s move. More precisely: because
| (i) | rotation distributes over bit-wise addition |
| (ii) | ZEROS is a fixpoint of any rotation, and |
| (iii) | we have to guarantee termination whatever rot’s dependence on its first argument, |
(2) |[ var i: int; i ≔ 1
; do t ≠ ZEROS →
t ≔ t ∔ rot.i.(ps.i) ; i ≔ i + 1
od
]| ,
viz. for all rot, and for all initial t. The gain of this rewriting is that it makes it easier to separate these two universal quantifications.
Consider now a terminating computation of (2) and let fi be the final value of i. Because ∔ is associative and ZEROS has the property
u ∔ v = ZEROS ≡ u = v ,
we can conclude that the carry-less sum of rot.i (ps.i) for 1 ≤ i < fi equals the initial value of t. Termination of (2) for any initial value of t is thus equivalent to stating that during execution of
(3) |[ var i: int; s: BV; i,s ≔ 1, ZEROS
; do i ≠ N →
s ≔ s ∔ rot.i.(ps.i); i ≔ i + 1
od
]|
with sufficiently large N, variable s successively takes on all possible value of type BV. Because type BV comprises 2n distinct values, “sufficiently large” is at least 2n. As we will show, we don’t need a larger value; for the rest of this note we choose
N = 2n
Now our challenge is to define N-1 values ps.i (1 ≤ i < N) such that, in the execution of (3), for any rotation function rot, variable s successively takes on all its N possible values. We shall solve the problem for n=1, and shall show how, from a solution ps for n, we can construct a solution ps′ for n′, provided n′=2n . We thus solve the problem for n an arbitrary power of 2.
Remark Since — as the reader may verify — the problem is unsolvable for n=3, there is probably no point in trying to be more ambitious. (End of Remark.)
For n=1, N=2 and ps.1=1 does the job: rotating a big vector of length 1 leaves it unchanged and in the one and only step of the execution of (3), the single bit s is inverted.
For n′=2n, type BV′ comprises the N′ bit vectors of length n′ with N′=2n′ or N′=N2. Variable s′ is of type BV′ and function ps′: int → BV′ is to be defined under the hypothesis that ps solves the problem for bit vectors of length n.
For the purpose of our discussion we introduce variables u,v: BV such that
s′ = u ⫲ v
(where ⫲ denotes catenation). The above relation implies that s′ determines the pair (u,v) and vice versa. We observe that this also holds for s′ and the pair (u ∔ v , v). (This observation captures the core of our solution.) In our solution, ps is used at two levels, so to speak. At one level — see below at "r = 0" — ps is used to generate all possible values for u ∔ v; at the other level — see below at "r ≠ 0" — ps is used to generate, for each value of u ∔ v and under invariance of it, all possible values for v. The two levels thus generate all (u ∔ v , v) pairs, i.e. all s′-values. More precisely, with 1 ≤ q * N + r < N2 ⋀ 0 ≤ r < N , ps′ is defined by
ps′.(q * N + r) = if r = 0 → ZEROS ⫲ ps.q
⫾ r ≠ 0 → ps.r ⫲ ps.r
fi
We have to check that the rotations in (3′) of bit vectors of length 2n can be interpreted as rotations of bit vectors of length n, so as to make ps applicable as generator of all BV values. On the first level, the symmetry of u ∔ v takes care of that, on the second level the symmetry of ps.r ⫲ ps.r does so.
For the sake of illustration, we tabulate ps for small values of n in fig.0. (For n=8, we give only the beginning of the table, which has 255 entries.)

In the column marked “ps” we have tabulated the ps-values as bit vectors of length n. In the column marked “gr” we have tabulated the corresponding “generators”, which are more compact characterizations of ps-values. Starting with a bit vector of length 1, consisting of a single 1, we can construct any ps-value by successively subjecting our bit vector to operation x or to operation y:
x: double its length by prefixing zeros y: double its length by catenating a copy
The generator records in order from right to left the sequence of operations that construct the ps-value. (Hence, 01010101 has generator yyx, while 00001111 has generator xyy.) Note that each y in the generator doubles the number of 1s in the bit vector.
For the sake of completeness we give a recursive definition, which is completely analogous to that of ps.
For n=1, gr.1 = “the empty string”; for n′, with 1 ≤ q * N + r < N2 ⋀ 0 ≤ r < N
gr′.(q * N + r) = if r = 0 → x⋅ gr.q
⫾ r ≠ 0 → y⋅ gr.r
fi
where x⋅ and y⋅ denote prefixing by the indicated singleton.
The advantage of generators is that they are nonredundant: not every bitvector is a ps-value, but every x/y-sequence is a generator. Generators, more precisely, the function gr will be explored for its own sake in the next section.
* *
*
The tabulated generators admit an alternative interpretation, viz. as identifiers of the bits whose inversions generate what is known as the “Gray Code”, e.g. for n=4:

That the Gray-Code table of width n and height N, as generated above, contains all N values, can be demonstrated by showing that any two entries in the table differ.
To this end we define for generators of equal length a total order < by the alphabetic order, i.e. with P and Q generators of equal length
(4a) x⋅P < y⋅Q (4b) x⋅P < x⋅Q ≡ P < Q (4c) y⋅P < y⋅Q ≡ P < Q
and now we can formulate
Lemma 0 In the sequence gr.i , h ≤ i < j with 1 ≤ h < j < N , the alphabetic minimum of the values in the sequence occurs exactly once.
Proof sketch In view of the recursive definition of gr, the proof is by mathematical induction on the length of the generator, with a case analysis in the induction step.
Either some value in the sequence starts with an x, or all values in the sequence start with y.
In the first case, (4a) tells us that we can configure our attention to the values of the form x⋅ gr.q ; the q-values being consecutive, (4b) thus reduces the demonstrandum for gr′ to the demonstration for gr.
In the second case we have a sequence of values of the form y⋅ gr.r with consecutive r-values; this time, (4c) performs the reduction.
(End of Proof sketch.)
Lemma 0 implies the absence of duplicates in the table we generated for the Gray Code: in the sequence of transitions that transforms the one entry into the other, the unique minimum identifies a position in which one inversion takes place, and in which therefore the entries differ.
* *
*
After the above interlude about the Gray Code, we return to our original problem. We have shown earlier that all the 5-values generated by (3) are distinct, whatever rotations for the ps-values are chosen, but now the obvious challenge is to prove this as well in a way analogous to our demonstration of the absence of duplicates in the Gray Code.
To this end, we associate with each generator its “patterns” and its “partition”; we discuss the patterns first. The patterns are the corresponding ps-value in its various rotations. For instance, generator yxy yields ps-value
00110011 (0, 1, 4, 5)
and by rotation the further patterns
01100110 (1, 2, 5, 6)
11001100 (2, 3, 6, 7)
10011001 (3, 4, 7, 0) .
Next to each pattern we have recorded — numbering them in the patterns from right to left — the bit positions of its 1s. They are of interest because, modulo n, their differences are unaffected by rotation. Note that the positions of the 1s in the ps-value are obtained by substituting in the generator 0 for x, and for each y a 0 or a 1, and reading the result as a binary number. For instance, in the above example, generator yxy yields 1s in positions 000(=0), 001(=1), 100(=4) and 101(=5).
The partition associated with a generator partitions the bit positions and has as many cells as an associated pattern has 1s. Each cell contains the values whose binary representations coincide in the y-positions of the generator. For instance, generator yxy yields the partition
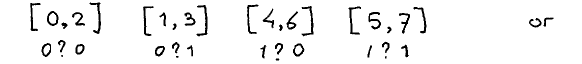
Lemma 1 An arbitrary pattern associated with a generator has exactly one 1 in each cell of the partition associated with that generator.
Proof Since the number of 1s in the pattern equals the number of cells in the partition, it suffices to show that no cell contains two 1s. We show this by demonstrating that no distance between two 1s in a pattern equals the distance between two positions in a cell of that partition.
We use two little theorems about binary arithmetic of natural numbers
(i) the least-significant 1 in the difference of two distance numbers occurs in a position where one of the numbers has a 1, the other a 0
(ii) two numbers whose least-significant 1s occur in different positions, differ.
The distance between two 1s in a pattern equals modulo n (which is a “higher” power of 2) the distance between two 1s in the ps-value (e.g. in our last example 7 - 0 = (8 + 4) - 5). The ps-value has its 1s in positions whose binary numbers have their 1s in the y-positions of the generator. From little theorem (i) we conclude that the least significant 1 in the binary representation of the distance between two 1s in a pattern occurs in a y-position of the generator.
By construction, a cell contains values that in binary only differ in x-positions of the generator, and thus we conclude from little theorem (i) that the least-significant 1 in the binary representation of the distance between two positions in a cell occurs in an x-position of the generator.
Thanks to little theorem (ii), the last two conclusions imply that no distance between two 1s in a pattern equals the distance between two positions in a cell of the partition.
(End of Proof.)
Lemma 2 Let generator G0 be alphabetically less than generator G1; then each pattern associated with G1 has an even number of 1s in each cell of the partition associated with G0.
Proof This proof is a little bit more complicated because the notion of alphabetic order has to be taken into account. The proof is by mathematical induction over the length of the generators. In base and step, P and Q are generators of the same length b and n = 2b.
Base The base case — see (4a) — are two generators whose left-most characters differ, i.e. G0 = x⋅P and G1 = y⋅Q .
By construction, the 1s in a pattern associated with y⋅Q can be grouped in pairs of 1s that are n apart. Also by construction, positions that are n apart occur in the same cell of the partition associated with x⋅P. From these two observations, the theorem follows for the base case.
Step Here — see (4b) and (4c) — we consider two generators whose left-most characters are equal. With P < Q we distinguish two cases.
(i) G0 = x⋅P ⋀ G1 = x⋅Q .
Patterns associated with x⋅Q are twice as long and have the same number of 1s as those associated with Q and are obtained from the latter by moving a number of its 1s at the right-hand side over n places to the left. In the transition from P to x⋅P, each cell is doubled in size by taking its union with the image obtained by moving it over n places to the left. Consequently, a new pattern has as many 1s in a new cell as some original pattern had in some original cell.
(ii) G0 = y⋅P ⋀ G1 = y⋅Q .
Patterns associated with y⋅Q are twice as long and have twice as many 1s as those associated with Q and are obtained from the latter by prefixing each pattern with a copy of itself. In the transition from P to y⋅P, cell size remains unchanged but their number is doubled: each original cell spawns the image obtained by moving it over n places to the left. Again a new pattern has as many 1s in a new cell as some original pattern had in some original cell.
And thus Lemma 2 has been proved for generators of arbitrary length. (End of Proof.)
Consider now a sequence of moves in (3). According to Lemma 0, there is in that sequence a unique move with the alphabetically smallest generator. Now focus on the parities of the cells of the partition of that generator. According to Lemma 1, that unique move changes these parities, while according to Lemma 2, all other moves leave them unchanged.
Acknowledgements I thank Rutger M. Dijkstra for drawing my attention to the problem and for generalizing four to any power of two. In matters of presentation I am endebted to the Tuesday Afternoon Clubs of Eindhoven and Austin.