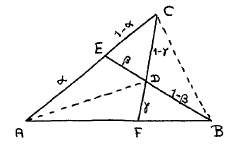
Given:
AE = α•AC
ED = β•EB
FD = γ•FC
Denoting with (PQR) the area of ΔPQR, we observe
(ADB) = γ•(ACB) and also
(ABD) = (1–β)•(AEB)
= (1–β)•α•(ACB)
from which we conclude γ = (1–β)•α .
[ The theorem we used thrice—say (PQR)•RS/QR = (PRS)—is no more than adding metric to —see EWD1221b—
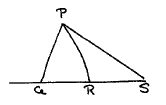
R ≠ S ∧ col.R.S.Q ∧ tri.R.Q.P ⇒ tri.R.S.P ]
The theorem proved in this note is of no importance; it is recorded here because I don't remember this proof technique from my school-days.
transcribed by Swarup Sahoo
last revisedSun, 26 Jun 2011
Nuenen, 22 December 1995
prof. dr. Edsger W. Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
transcribed by Swarup Sahoo
last revised