Two problems derived from Hugo Steinhaus

Given 4 points in the Euclidean plane such that their 6 mutual distances are all distinct. (Note that this implies that the 4 points are distinct.) We connect by a drawn line segment any pair of points of which one is the nearest neighbour of the other. Show that no drawn segments intersect each other.

If the points are not the vertices of a convex quadrangle:

the 6 connecting segments don't intersect at all, so no matter which connections are drawn, the theorem holds.

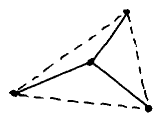
If the points are the vertices of a convex quadrangle, e.g.

the only intersecting pair is formed by the diagonals, and it therefore suffices to show that at least one of the diagonals is dotted, i.e. that at neither of its ends it is the shortest connection.

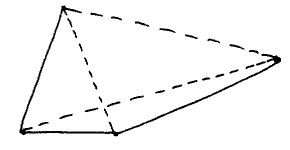
I have seen several arguments, including a wrong one by myself, in terms of lengths alone; in one way or another they all used the triangular inequality. Not so the argument by Lyn Pierce, which was the shortest of them all.

A diagonal is an edge in two triangles, and it is dotted if it is the longest side of one of those triangles. It is so if, in that triangle, it is opposite to the largest angle. Because the 3 angles of a triangle add up to 180° (and are positive), an angle ≥90° is the triangle's largest. Because the 4 angles of a quadrangle add up to 360°, at least one of them is ≥90°, and hence at least one of the diagonals is dotted, viz. the one "opposite" to a largest angle of the quadrangle. A very nice, constructive existence proof! I was pleased to see "maximum ≥ average" used in a setting different from the pigeon hole principle. Steinhaus, needless to say, gave a proof by contradiction.

* *
*

We consider the various (viz. n! to be precise) ways in which one can nail a wire exactly once on each of n posts, put at equal distance along a straight road.

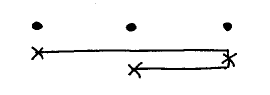
When one wishes to minimize the length of the piece of wire used, one starts at one end, and nails the wire on the posts in order, e.g. (n = 5, and each x standing for a nail)

Five fenceposts strung together in-line.

But what if we want to maximize the length of wire? For n = 3, the solution is obviously (apart from reflection)

Three fenceposts with one wire doubling back for maximum length.

and for n = 4 (after a moment's thought)

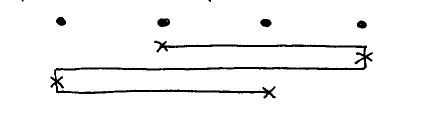Four fenceposts with wires folded twice for maximum length.

but how is it for general n?

The crucial observation is that in a maximal arrangement, at no post the situation

A nail where the wire goes straight through.

occurs: the wire could have been lengthened by removal of the above nail and connecting the above post to one of the posts where the wire currently ends. This observation leads to the

Lemma 0. At each nail, the wire ends or reverses direction.

In other words — in pictures, to be precise — nails only occur in the following 4 positions

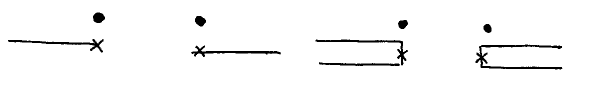Wire to the left, wire to the right, wire doubling left, wire doubling right.

We now mark the zones before, between, and after the posts with their "intensities", i.e. the number of

Zones marked with intensities on the n = 4 solution.

wires passing through each zone. This terminology (with Lemma 0 and the fact that the wire has 2 ends) allows us to formulate

Lemma 1. At two posts, the intensity changes by 1, at all other posts it changes by 2.

The length of the wire equals the sum of the intensities. We maximize this sum when, going in from the outside (where the intensities are 0), we increase the intensities each time by the maximum amount 2 until near the center we accommodate the two changes = 1.

For even n (odd number of zones), the sequence of intensities is unique, e.g. for n = 6 : 0 2 4 5 4 2 0 .

For odd n (even number of zones) there are two solutions which are each other's mirror image, e.g. for n = 7

0 2 4 6 5 4 2 0 and
0 2 4 5 6 4 2 0 .

The sequence of intensities does in general constrain but not determine the shape of the wire: in terms of the wire, the solution is in general far from unique. The above problem is closely related to "The problem of the difficult dartboard" (see EWD1045, dd 27 February 1989).

The problems come from Hugo Steinhaus, "One Hundred Problems in Elementary Mathematics". Dover Publications Inc, New York, 1979