The angle bisectors of a triangle
Renewed interest in EWD1014 induced me to look for a nice derivation of the formula for the lengths of the angle bisectors in a triangle. In doing so, I had a few small surprises, but just enough to justify this note.
* * *
There is, to begin with, the theorem that the angle bisector divides
the opposite side into the same ratio as the adjacent sides, in terms
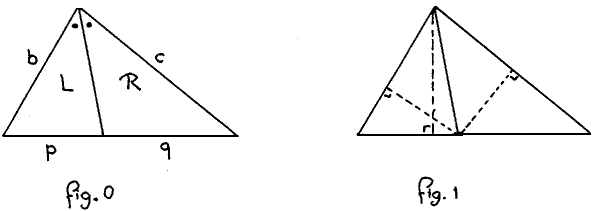
of the annotation in fig.0 for instance
(0) p/q = b/c(The usual proof of (0) is by remarking that both expressions equal L/R where L and R denote the areas of the left and right subtriangle respectively; p/q equals L/R because — see fig.1 — the subtriangles share the same (vertical) altitude, while b/c equals L/R because the two remaining altitudes drawn in fig.1, since they intersect on the angle bisector from the top, have the same length.)
We introduced (0) with the clause "for instance" because alternative formulations are
q/p = c/b , b/p = c/q and p/b = q/c ;please note that these 4 formulations equate 4 different values, while there is no reason to prefer one over the other. Compared to the above four, the fifth
(1) p∙c = q∙bis canonical! It is a striking example of how much nicer the symmetric product is than the quotient, whose asymmetry creates a spurious diversity. (This in addition to the problems that, in general, may be created by the fact that the quotient is a partial function.) In what follows, we shall use (1).
* * *
Next our attention turned to the angle bisector itself. We named it
d, as in fig.2:
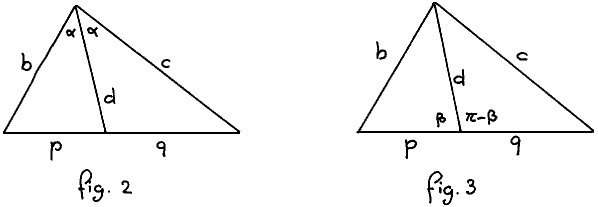
The two angles known to be
equal we named α, and our purpose was to apply the Cosine Law to
both subtriangles and then to eliminate α. We observe
p2 = b2 + d2 − 2∙b∙d∙cos.αmultiplying the former by c and observing — see (1) — p2∙c = p∙q∙b, multiplying the latter by b and similarly observing q2∙b = p∙q∙c and subtracting we get
q2 = c2 + d2 − 2∙c∙d∙cos.α
p∙q∙(b-c) = b∙c∙(b−c) + d2∙(c−b)Dividing out the common factor (b−c) we get (as intended)
(2) d2 = b∙c − p∙q ,but the problem with the last step is that it does not work in the case b=c.
It was Rajeev Joshi who observed that there is no need to take again into account that the two angles at the top are equal because (1) already captures that we are talking about the angle bisector of the top. Applying the Cosine Law — see fig.3 — and using cos.(π−β) = -cos.β, we obtain
b2 = p2 + d2 − 2∙p∙d∙cos.βmultiplying the former by q and the latter by p and observing, thanks to (1), this time q∙b2 = p∙b∙c and p∙c2 = q∙b∙c, and finally adding, we get
c2 = q2 + d2 + 2∙q∙d∙cos.β
(p+q)∙b∙c = (p+q)∙p∙q + (p+q)∙d2,which yields (2) without the exception. Not using the equality of the angles at the top a second time is the other charm of the latter argument.