EWD35 translated. Original is here .
About the sequentiality of process descriptions.
It is not unusual for a speaker to start a lecture with an introduction. As some in the audience might be totally not familiar with the issues that I wish to address and the terminology, which I will have to use, I will to give two examples as a means of introduction, the first one to describe the background of the problem and a second one, to give you an idea of the kind of logical problems, that we will encounter.
My first introduction is a historical one. Firstly I want you to understand what a sequential process description is. An example of a sequential process description that you all know is the construction of the altitude from the vertex C of the triangle ABC. This description might read as follows: 1) draw the circle with centre A and radius = AC; 2) draw the circle with centre B and radius = BC; 3) draw the line, which is determined by the intersections of the circles mentioned under 1) and 2). This description is for the benefit of those unfamiliar with the construction of the altitude line; for their benefit the construction of the altitude line consists of a number of actions of a more limited repertoire; actions, which may be executed in the specified order, one after the other, i.e. sequentially. It will not have escaped the attentive reader, that here we have specified more than strictly necessary: it is essential for action 3) to be carried out only after operations 1) and 2) have been completed; operations 1) and 2) may however be carried out in reverse order, or even concurrently by a drawer who can operate two compasses, lets say one in each hand, executing actions 1) and 2) simultaneously. But this freedom has disappeared entirely from our process description.
Now for a more numeric example, something more in line with the area, where the problems soon be treated have become actual. Given the values of the variables a, b, c and d, asked to calculate the value of the variable x, given by the formula "x = (a + b) * (c + d)". When performing this value assignment is not part of the primitive repertoire of the calculator – and you may by now start thinking of a calculator machine – , then this calculation rule should be constructed from more elementary steps such as:
Calculate t1: = a + b;
Calculate t2: = c + d,
Calculate x: = t1 * t2.
This calculation rule contains exactly the same over-determination as our altitude construction: the order of the first two steps is irrelevant, they could even be carried out simultaneously. The above process description is representative of the execution mode of more traditional computing machines. The repertoire of elementary operations, because technical components are required for every operation, is finite and for financial reasons even very limited; these calculators owe their enormous flexibility to the fact, that arbitrarily complex algebraic expressions as above illustrated can be broken down in a sequence of these elementary operations. Inherent to this sequential description of the process is, that one specifies more than strictly necessary. This has not been a problem for some time, but in recent years this has changed. This is due to two reasons: changes in the structure of machines and the advent of a new class of problems, where these machines are to be used.
The classical sequential machine does "one thing at a time" and performs one function after another. For the sake of efficiency many specific devices were built for specific functions, but if you hold on to carrying out the different operations strictly sequential, suddenly the machine presents itself as N cooperating bodies, of which only one or two are working at any discrete moment. If N is large, this means that most of your machine most of the time stands idle and that is clearly not the intention.
The second reason is the advent of a new category of problems; computing machines were originally only used for fully predefined processes, and the machine could execute the process on its own at its own pace. As soon as one wants the information processing method to cooperate with some other process – e.g. a chemical process, which must be directed by the computing machine – then very different types of problems occur. Referring to our example of the calculation of x: = (a + b) * (c + d) we no longer are in the situation that it does not matter, which sum is created first. If the data a, b, c and d are provided at unknown moments by the environment of the computing machine and it is the task of the machine, to deliver on the value of x as soon as possible, this means that the machine should initiate with a partial calculation as soon as the necessary information is available: which sum one wants to be calculated first, will depend on the sequence in which the data a, b, c and d become available. This was my first introduction and with it I hope to have given you an idea of how you should visualize a sequential process description, and why there is a need for less strict sequential process descriptions.
Now my second introduction, which is meant to give you right from the start an idea of the logical problems, we will run into by leaving the strict sequentiality. Just as in an ordinary piece of algebra variables are identified with letters, generally "names", in the actions of information processing one has the continuous duty to identify, the duty to find the object defined by a name. Under circumstances one would like to have the selection process, which the teacher in the classroom has, when she says "Johnny, come to the black board." Assuming that the class as a whole pays attention and obeys, this process works flawlessly under the assumption that there is one and only one Johnny in the classroom. The particularity of this selection mechanism is that it works regardless of the number of children in the classroom. Unfortunately this idyll cannot be implemented technically or at the most with flaws and we have a problem, which is more in line with reality, when children do not spontaneously respond to calling their name and Miss, when she wants Johnny to the board, is forced to take Johnny by the ear and drag him to the board. If it is an old fashioned school, where every child has its own place in the classroom, then the teacher can, when at the beginning of the year she has put the children on a particular place, rename them for her own convenience, and replace the name "Johnny" – which for finding the boy is not very helpful – by an identification, which, according to its structure immediately defines which ear she should pull: she can call the boy "third row, second desk". This is essentially the technique that is used in classical automata by classical applications. In modern applications one can not do this, and one must cope with such problems, as Miss has, when the children can choose where they sit. To make it not impossible for Miss, we assume that a name label has been pinned on each of the obstinate children. If the teacher now wants Johnny to the board, she has to look up Johnny. The teacher works sequentially, can only read a label at a time, and the teacher works systematically: she ordered the desks for her self uniquely in one way or another and if she wants Johnny, she visits the desks in this order, always asking herself "Are you Johnny?", if not, then she goes to the next desk. This process works flawlessly, if we can guarantee that the children do not change positions during the walk of the teacher, if we can guarantee that the two processes "child localization" and "child permutation" are not performed simultaneously. Because also you understand that Johnny, as soon as he realises, that he is the wanted figure, sits down in the back of the classroom and when the teacher searched the front half of the class, he jumps quickly forward. We can refine the teacher and make her, if she has searched the whole class and did not find Johnny, start all over from the beginning, but this is no solution, because Johnny immediately would jump back again. Now you might remark that if those permutations were not executed with so much malice but only randomly, then in that case the expected time for locating Johnny remains finite, his freedom of jumping around did not even increase it. This remark, how hopeful, brings no solace. Those who have studied the "Theory of computability" know how much weight is given to a finite, i.e. guaranteed to end algorithm, and they will understand that a process that potentially spins indefinitely, is no attractive element. Worse is, that in reality it is often a question, whether we are allowed to consider the permutations of the children as random. If the probability is finite, that when the teacher has made her round through the class, the children are seated exactly as when the teacher began to search, this could really be the first period of a pure periodic phenomenon. Even if we accept the risk that we will never find Johnny, still her misery does not stop here, because in addition to the risk that she will not find Johnny, she runs the much greater risk that she drags the wrong child to the board, i.e. when the children between the moment that she satisfactorily ascertains "So, you are Johnny" and the moment that she, based on the findings, stretches out her hand to the corresponding ear, swiftly change places. In an information processing system this would be tantamount to a disaster. This is the end of my second introduction, which I hope gave you some idea of the kind of problems that we will encounter.
At the end of my first introduction I mentioned two reasons which were responsible for a growing interest in less strictly sequential process descriptions. I've only slightly touched on them and it is you may not have noticed that they were derived from almost opposite entourage. In the first case I mentioned the increasing complexity of machines, which now are composed of a number of more or less autonomous working parts with the assignment to work together to execute one process. In the second case, where we looked at the machine in a so-called "real-time application", then we had a view of a single device that had the possibility, in case of a change in the external urgency situation, to switch to the now most urgent of its possible tasks. These two packages, a cooperation of a number of machines in one process and conversely, one machine dividing its attention on a number of processes, have long been regarded as alien to one another. They have even invented different names for it, one called "parallel programming" and the other called “multi programming”. You should not ask me what's what, because I can not remember that, since having discovered that the logical problems, that they evoke by the non-sequentiality of the process definition, are in both cases exactly the same.
In the next part I will use the view of a number of mutually weakly coupled, in itself sequential machines, following the first entourage. But this is only a way of describing, because that what I will call a machine from now on is not necessarily a discrete identifiable piece of equipment; from now on my distinguished machines may be very abstract and they represent no more than a standalone sequential subprocess. This is partly reflected in my showing a predilection for a cooperation of N machines, N random. If I only used the term machine for a sensible functional piece of equipment, then I might consider the number of machines for each installation as fairly constant. Now that a machine, as personification of a standalone sequential subtask, may be created ad libitum by the user, such a fixed upper limit is no longer acceptable. So I'm going to talk about the cooperation of N machines, N not only arbitrary, but if it has to be, variable during the process. Superfluous machines can be destroyed, new machines can be created as needed and included in the cooperation of the others. I hope, that you will accept, now on my authority or afterwards by your own recognition, that we can limit ourselves without harming the generality to sequential machines, which execute some cyclical process.
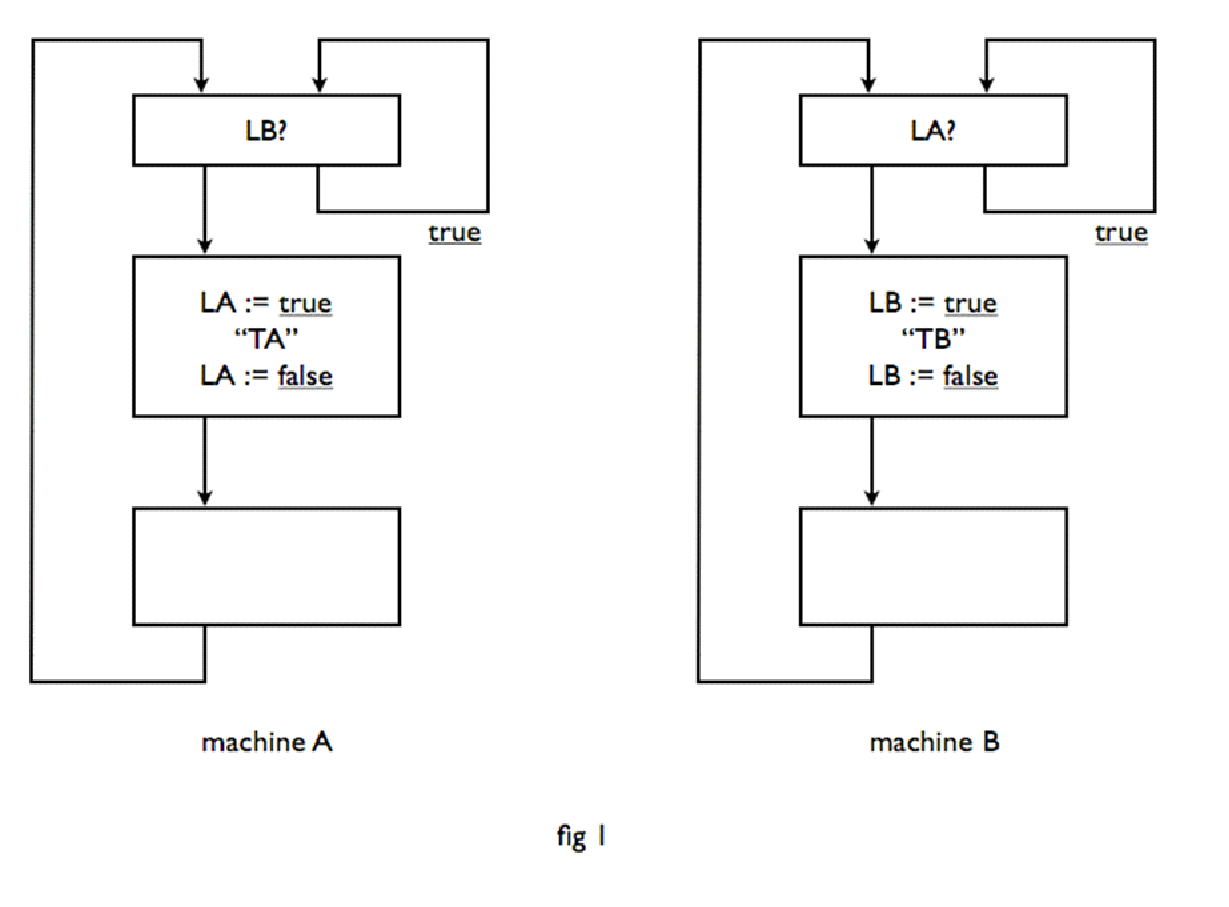
Let us start with a very simple problem. Given two machines A and B, both engaged in a cyclical process. In the cycle of machine A there is a certain critical section, called TA, and in that of machine B a critical section TB. The task is to make sure that never simultaneously both machines are each in their critical section. (In terms of our second introduction: A machine could be the teacher, trajectory TA the selection of a new student, to be called to the board, while the trajectory TB represents the process "child permutation".) There should be no assumptions made on the relative speeds of the machines A and B; the rate at which they work does not even need to be constant. It is clear that we can realize the mutual exclusion of the critical section only, if the two machines are in some way or another able to communicate with each other. For this communication, we establish some shared memory, i.e. a number of variables, which are accessible to both machines in either direction, i.e. to which both machines can assign a value and whose current value may be found out by both machines. These two actions, assigning a new value and inquiring about the current value are considered indivisible actions, i.e. if both machines wish to "simultaneously" assign a value to a common variable then the value assigned at the end is one or the other value, but not some mixture. Similarly, if one machine asks for the value of a shared variable at the time that the other machine is assigning a new value to it, then the requesting machine will receive or the old or the new value, not a random value. It will show that for this purpose we can limit ourselves to common logical variables, i.e. variables with only two possible values, which we following standard techniques denote with "true" or "false". Furthermore, we assume that both machines can only refer to one common variable at one time and next only to assign a new value or to inquire after the current value. In Figure 1, a tentative solution is given in block diagram form for the structure of the program for both machines. Each block has its entrance at the top and its exit at the bottom. For a block with a dual output, the choice is determined by the value of the previously requested logical variable: has it the value true, then the output right intended, has a value of false, then we choose the exit left.
There are two common logical variables in this diagram, LA and LB. LA means machine A is in its critical section, LB means machine B is in its critical section. The schemata in Figure 1 are obvious. In the block top machine A waits if he arrives at a moment, that machine B is busy in section TB, until machine B has left its critical section, which is marked by the assignment "LB: = false", which next lifts the wait of machine A. And vice versa. The schemata may be simple, they are unfortunately also wrong, because they are a bit too optimistic: they don't exclude that both machines simultaneously enter their respective critical sections. If both machines are outside their critical section – say somewhere in the block left blank – then both LA and LB false. If now simultaneously they enter in their upper block, they both find that the other machine does not impose any obstacle in their way, and they both go on and arrive simultaneously in their critical section.

So we have been too optimistic. The error has been that the one machine did not know, whether the other was already inquiring about his state of progress. The schemata of Fig. 2 make a much more reliable impression, and it is easy to verify that they are totally secure. e.g. machine A can only start to execute section TA, after, while LA is being true, it has been verified that LB is false. No matter how soon after the knowledge of this fact to machine A becomes obsolete, because machine B in its upper block performs "LB = true", machine A can safely enter section TA, because machine B will be neatly held up until after finishing section TA LA is being changed to false. This solution is perfectly safe, but we should not think that with this we have solved the problem, because this solution is too safe, i.e. there is a chance that the whole teamwork of these machines halts. If they run the upper block in their schema simultaneously, then both machines run in the subsequent wait and continue into eternity of days politely facing the same door, saying, "After you", "After you".

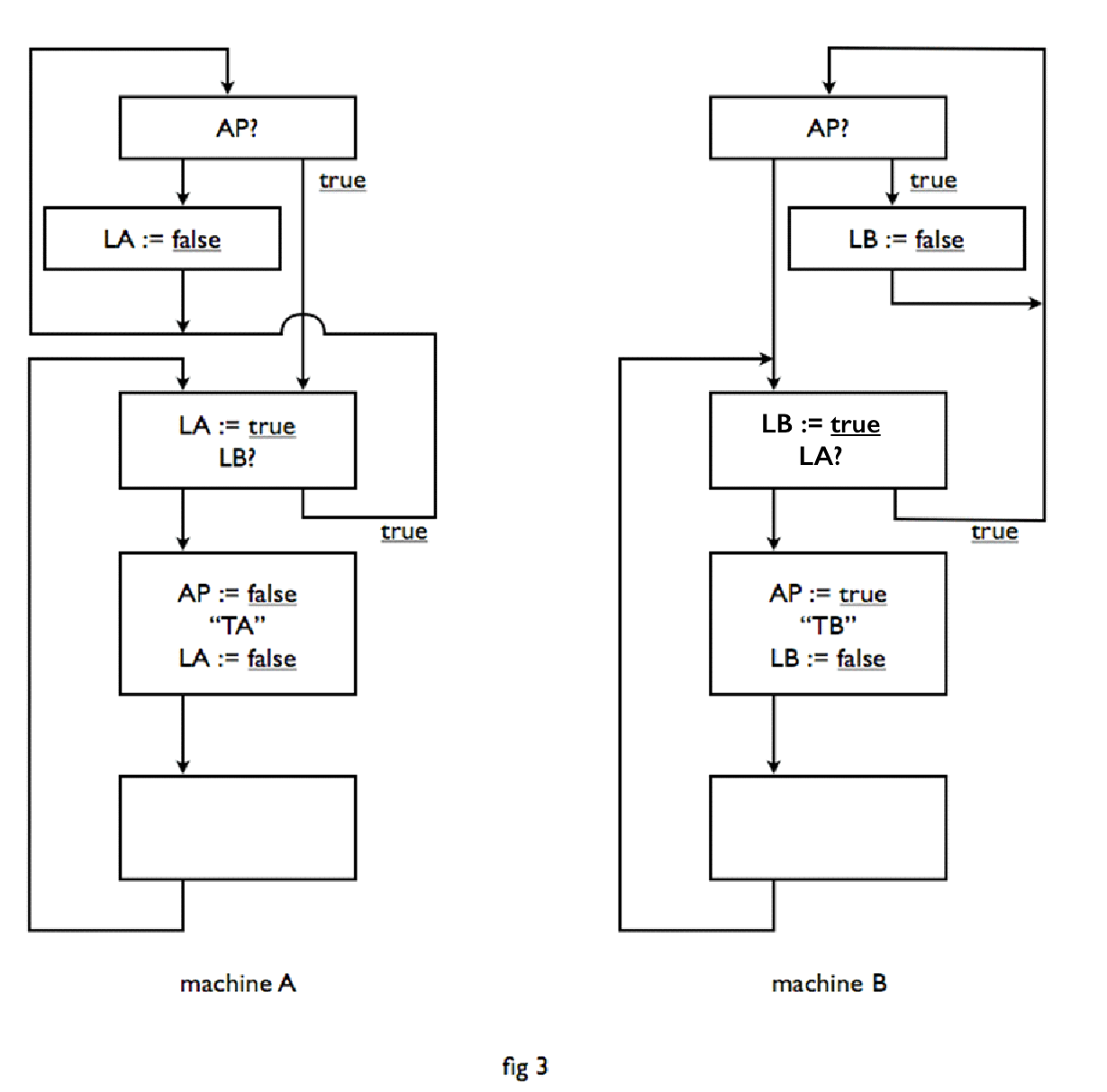
We have been too pessimistic. You see, the problem is not trivial. It was to me at least, after these two try-outs, not at all obvious that there was a safe solution, that did not also contain the possibility of a dead end. I have passed the problem in this form to my former colleagues of the Computational Department of the Mathematical Centre, adding that I did not know if it has a solution. Dr. T. J. Dekker has the honour of being the first to have found a solution, which was also symmetrical in both machines. This solution is shown in Figure 3. A third logical variable is being introduced, namely AP, which means that in case of doubt machine A has priority. Due to the asymmetric significance of this logical variable, portions of these programs more or less mirror each other, but functionally the solution is, however, completely symmetrical and no one machine has a precedence over the other. To prove that this solution conforms to the stated requirements, we first observe that the sections TA and TB are preceded by the lock, which we have already identified in Figure 2 as safe. Simultaneous execution is thus impossible. We only need to verify that it is also impossible that both machines keep waiting before their critical section In these wait cycles, the value of AP will not be changed. If we restrict ourselves to the case that AP is true, then machine A can only continue cycling if also LB is true; under the condition AP true machine B though can only remain running in the cycle, that sets LB to false, i.e. that forces machine A out of its cycle. In the case of the AP false the analysis follows in the same way. As AP as a logical variable is or true or false, thus the possibility of eternal waiting for each other is also excluded. Q.E.D.
Dekker's solution dates back to 1959 and for almost three years, this solution has been considered a "curiosity", until these issues at the beginning of 1962 suddenly became relevant for me again and Dekker's solution acted as the basis of my next attempts.
The problem had by now changed drastically. In 1959, the question was of whether the described capability for communication between two machines made it possible to couple two machines such, that the execution of the critical sections was mutually excluded in time. In 1962, a much wider group of issues was considered and the question was also changed to "What communication possibilities between machines are required, to play this kind of games as gracefully as possible?"
Dekker's solution was used as a starting point in different ways. As it is unclear in this solution, what one should do, when the number of machines increases, and the challenge remains to ensure that at any time there is only one critical section treated, it was an incentive to find other ways. By analysing the difficulties that Dekker had to overcome, we could get a clue what would be a more hopeful path to follow.
The difficulties arise because if one of the machines inquired after the value of a common logical variable, this information can immediately afterwards already be obsolete, even before the informing machine has effectively acted upon it. In particular: before the informing machine has had the possibility to inform its partners that he "has taken a snapshot" of the value of a shared variable. The hint, which can be extracted from this reflection is that one should look for more powerful "elementary" operations on the common variables, in particular for operations, in which the limit of one-way information transmission between the machine and shared memory no longer applies.
The most promising operation, we could think of, is the operation "falsify". This asks after the value of a logical variable and the fact that this operation is performed is revealed in half of the cases. The operation falsify exits, forcing the logical variable, which it operated on, with value "false".
The operation "falsify" can be defined as follows:
"Boolean procedure falsify (S); boolean S;
begin boolean Q; falsify := Q := S; if Q then S: = false end ",
provided we hereby state that the operation falsify, in spite of its sequential definition should be considered as a elementary instruction of the repertoire of machines. Where "elementary" in this case means that during the execution of falsify by one of the machines the logical variable in question is considered inaccessible to all other machines.
That this operation is a step in the right direction, follows from the fact that we immediately have the solution for a cloud of machines X1, X2, X3, . . . , each with its critical path TXi, that all have to exclude each other in time. We can play this with one common logical variable, say SX indicating that none of the machines is executing its critical path. The programs now all show the same structure:
"LXi: if non falsify (SX) then goto LXi; TXi; SX := true; process Xi; goto Lxi"
note, that in the programs for the separate machines Xi nowhere is it stated, how many machines Xi actually exist: we can by merely adding, expand the cloud of machines Xi.
The programmed wait cycle that exists herein, is of course very nice, but it did little to what our goal. A tiny wait cycle is indeed the way to keep a machine busy "without effect" . However, if we consider now, that will be the majority of these machines will be simulated by a central computer so that any action in one machine can only be performed at the expense of the effective speed of the other machines, then it is very costly using a wait cycle to demand attention of the central computer for something completely useless. As long as the wait cycle cannot be exited, in our opinion the speed of this machine may be reduced to zero, To express this we introduce a statement instead of wait cycle, a basic instruction in the repertoire of the machines, that may take a very long time. We indicate this with a P (to Pass); in anticipation of future needs, we represent the statement "SX: = true" by "V(SX) – with V of “vrijgave” (in English: release) (This terminology is taken from the railway environment. In an earlier stage the common logical variables were called "Semaphores" and if their name starts with an S, it is a reminiscence of it). The text of the programs in this new notation is as follows:
"LXi: P(SX); TXi; V(SX); proces Xi; goto LXi" .
The operation P is a tentative pass. It is an operation, which can only be terminated at a time, when the associated logical variable has the value true, termination of the operation P also implies, that the value of the associated logical variable is again set to false. Operations P can be carried out simultaneously, the termination of a P-operation however is considered as an indivisible event.
The introduction of the operation V is more than introducing a shorthand notation. Because, when we still had the wait cycle using the operation falsify, the individual machines had the duty to detect the equalization to true of the common logical variables, which were waiting for the event and in that sense waiting was a fairly active business for a relatively neutral event. With the introduction of the P-operation as we more or less achieved, that we say to a machine, which temporarily has to stop, "Go to sleep, we will wake you up when you can progress." But this means that assigning true to a common logical variable, for which there might be a machine waiting, no longer is a neutral event like any other value assignment. Here namely we might have to attach the side effect, that one of the "dormant" machines should be “woken”. It means that the logical variables, which while being false might be blocking one or more machines, need not be permanently monitored for, but only when the transition to the value true will be signalled to a “central alarm-clock”. If the "central alarm-clock" keeps record for each common logical variable, which machines are waiting in this moment for each logical variable, the central alarm-clock can, if it is explicitly alerted on becoming true of one of those common logical variables, decide quickly, whether this transition is a motive to wake up a sleeping machine and if so which one. The operation V can now be considered as a combination of assigning the value true to a semaphore, plus alerting the central alarm clock on this event. It is clear that this central alarm-clock can not function, if we allow that the common logical variables may also be changed privately, "secretly", by normal value assignments (of the neutral type "S := true"). To underline this ban, I call the common logical variables from now on "semaphores" and I demand, that the only way, in which a machine will be able to communicate with an existing semaphore, will be the P-operation and the V-operation.
And herewith the operation "falsify", which by the attractiveness of its simplicity for our comprehension has been so helpful, has again disappeared from the scene and the question is justified, whether we with the introduction of the semaphore, that is only accessible through the operations P and V, have not thrown the baby out with the bathwater. This fortunately is not the case. By removing the operation "falsify" from the basic repertoire of the various machines and to replace it by the operations P and V, we have lost nothing: be the introduction the operations P and V no empty gesture, there must be at least one semaphore, on which they can operate. This one semaphore – call him "SG", the Semaphore-General – is sufficient to add the operation falsify on any common logical variable to the repertoire of all machines. Because:
If we define in each machine:
"boolean procedure falsify(GB);
boolean GB;
begin boolean Q;
P(SG); falsify := Q := GB;
if Q then GB := false; V(SG)
end"
and we furthermore agree that any reference to a common logical variable will be encapsulated between the statements "P(SG)" and "V(SG)" (such that the assignment "GB1 := true" in each machine will now have the form "P(SG); GB1 := true; V(SG)", we have ensured that we comply to the secondary condition, that “the logical variable in question during operation falsify by one of the machine is inaccessible for all other machines”. We did not shoot ourselves in the foot with the barter.
We now will show that the operations P and V in their scope are not limited to mutual exclusion, but that we can use them to synchronize two machines with each other. Suppose that we have two cyclic machines, say X and Y, each in their cycle has a critical section, say TX respectively. TY, wherein the requirements are as following:
1) the execution of the critical section TX may in time not coincide with that of TY;
2) the execution of the sections TX and TY must be alternating events (to this condition we were referring when we spoke of "mutual synchronization").
If you want to imagine an entourage, in which one is placed before this problem, then think about the following. Process X is a number generating process (a calculation process), process Y is a number consuming process (a typewriter) and these two processes are linked by a "counter" having the capacity of one digit. The action TX is to deposit the next digit to type on an empty counter, the piece TY represents the pick up of the digit from the full counter. The strict alternation arises from the requirement that on one hand none of the offered digits to the counter "may be lost" but has necessarily to be typed, and on the other hand – if for some time there is no offer is – the typewriter should not go about filling his time by yet again type the last digit.
We can accomplish this with two semaphores, say SX and SY, where: SX now means that first it is section TX's turn, and SY means that first it is section TY's turn. For machines X and Y programs now read:
"LX: P(SX); TX; V(SY); proces X; goto LX" and
"LY: P(SY); TY; V(SX); proces Y; goto LY".
We can immediately extend this in two different ways. If we exchange the machine X by a cloud of machines Xi, who all want to use the same counter to discharge their production and exchange the machine Y replaced by a cloud machines, all of which are willing to take of the information off the counter(regardless by which the machines Xi it was placed there, therefore the image of typewriters is no longer suitable), then the programs for machines Xi and Yj read in analogy to the above-programs:
"LXi: P(SX); TXi; V(SY); proces Xi; goto LXi" and
"LYj: P(SY); TYj; V(SX); proces Yj; goto LYj" .
If we had also had a group of machines Zk, and had the problem been, that the implementation of a TX-section, a TY-section and a TZ-section should follow each other cyclical in that order, then the programs read:
"LXi: P(SX); TXi; V(SY); proces Xi; goto LXi" and
"LYj: P(SY); TYj; V(SZ); proces Yj; goto LYj" and
"LZk: P(SZ); TZk; V(SX); proces Zk; goto LZk" .
We note here, that in the last two examples the machines Xi are equal: they represent only that the process TX has to be inter-spaced by something, they leave the question open, how complex these intermediate operations will be realized.
The next task may prove that our operations P and V in their current form are not quite powerful enough. We consider therefore the following configuration. We have two machines A and B, each with their critical section TA respectively TB; these sections are completely independent of each other, but there is a third player, machine C, with its critical section TC and the execution of TC may in time not coincide with that of TA, nor with that of TB. We can do this with two semaphores say: SA and SB. For machines A and B, the program is simple, namely
"LA: P(SA); TA; V(SA); proces A; goto LA" and
"LB: P(SB); TB; V(SB); proces B; goto LB" ,
but for machine C the next program is although safe, unacceptable:
"LC: P(SA); P(SB); TC; V(SB); V(SA); proces C; goto LC" .
In fact: machine C might have successfully completed the statement P(SA) at a time, that machine B is busy in section TB. As long section TB is not yet completed, machine C can not continue – that is correct – but also machine A can no longer execute his section TA and that is not correct: indirectly, via C machine here the sections TA and TB are yet again coupled. The operation P(SA) of machine C hastily put the semaphore SA to false, thereby hindering A machine unnecessarily.
We will therefore extend the operations P and V to operations, to which we can offer an arbitrary number of arguments – exceeding the limits of ALGOL 60, but that does matter very little in this context. For the V operation the meaning is clear: it is no different than the simultaneous assignment, which assigns the value true to all semaphores passed. The P-operation with a number of arguments, eg "P(S1, S2, S3)", is an operation which can terminate only at the moment, that all semaphores passed have the value true (in our example therefore the moment when is valid: "S1 and S2 and S3"), termination of a P-operation in this context implies that simultaneously a value of false is assigned to all semaphores. And after this expansion the termination of a P operation is again considered an indivisible event.
With this extension, we are able to define machine C such, that the signalled objection no longer presents itself:
"LC: P(SA, SB); TC; V(SA; SB); proces C; goto LC".
Finally I wish to show, although this is certainly not the application for which the P and V operations are designed, how this will allow us to calculate the dot product of two vectors, without committing us to the order in which the products of the elements are added together.
Suppose that we wish to calculate the sum SIGMA (i, 1,5, A [i] * B [i]) – in words, the sum, for i from 1 to 5, of (A [i] * B [i]) -; Suppose that have been introduced the 7 semaphores: Ssom, Sklaar and five semaphores Sterm [i] with i = 1,2,3,4 and 5; all 7 with the initial value false;
Suppose, that already have been created five machines with the structure (i = 1,2,3,4,5):
"Lterm[i]: P(Ssom, Sterm[i]);
scapro:= scapro + A[i] * B[i];
n:= n – 1;
if n = 0 then V(Sklaar) else V(Ssom)
goto Lterm[i] " ,
all executing their – only – P-operation;
Consider now a sixth machine, that under these conditions will begin the following statements:
". . .; n:= 5; scapro:= 0;
V(Ssom, Sterm[1], Sterm[2], Sterm[3], Sterm[4], Sterm[5]);
"program, that does not modify names semaphores, scalars en vector elements";
P(Sklaar);. . "
After the last P-operation of the sixth machine is finished, n has the value 0, scapro the value of the requested sum and all semaphores and five former machines are returned in their original condition.
transcribed by Gerrit Jan Veltink
translated by Martien van der Burgt and Heather Lawrence