Understanding Gradient Descent Using Toy Models

Although gradient descent is a nifty little algorithm, it is unfortunately very slow. In order to speed it up, we may seek to modify the gradient - stepping in the direction it points at either slower or faster, or maybe in a different direction altogether.

In order to achieve this, we can bring in the generalization that our gradient descent step looks like:

theta_t+1 = theta_t - f(grad L(theta_t))

The simplest example of such a function would be

f(x) = epsilon * x, for epsilon > 0

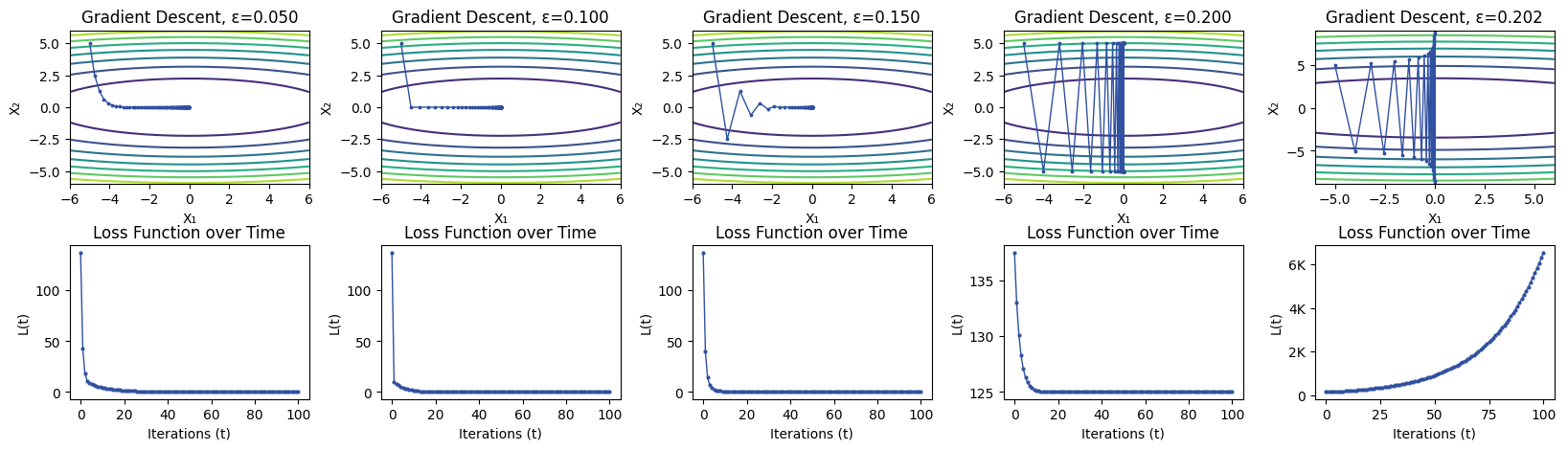
That is, simply scaling the size of our gradient. Since this only increases or decreases the magnitude of the gradient without changing the direction, epsilon corresponds to the size of the steps we take; higher values of epsilon will make us take larger steps across the parameter space, while lower values of epsilon will make us take smaller steps. As a result, epsilon is also referred to as the step size parameter.

Different values of epsilon can result in different end-behavior of the algorithm. Consider the simple example of a 3d parabaloid, displayed as a contour plot below