Applying Inverse Kinematics to Animate Molecules
Goal
The goal of this
project was to use some of the inverse kinematics techniques to generate
molecular configurations for a known molecule.
These configurations can be viewed in a browser to observer conformation
changes as a molecule changes its shape.
Background
Inverse kinematics is
a widely used technique in robotics to compute rotational angles between joints
for a given set of links, their starting position, and the desired position for
the end effector [1]. Several papers
have been written on how a molecule can be modeled as a robot [1], and how this
model can be used to solve inverse kinematics equations for molecules. These solutions can be extremely useful in
solving protein folding and protein docking problems [1]. For details refer to [6].
Tasks
There are three main
tasks associated with this project:
- Model a molecule as a series of links so
that the inverse kinematics algorithm can be used to compute new position.
- Use the inverse kinematics algorithm designed
by Young-In (Human body project’s team member) to calculate new
configurations.
- Export the new configurations to a file
format readable by the Perfly browser.
As most molecular
inverse kinematics techniques are being studied to solve protein docking or
folding problems, I focused on the “Anthrax Antigen” protein
Modeling the Molecule
According to Kavraki
[1], most molecular kinematics studies treat van der Waals radii, electric
charges, bond lengths, and bond angles as constants, and only allow the
torsional angles to change. However,
determining the torsional angle was a major challenge.
The source for the protein
I used was the PDB databank [3]. A PDB
file only contains the atom type and its co-ordinates, so I had to compute the
links based on that information alone.
Protein Structure
A protein can
be thought of a long train of amino acids linked together. Amino acids are chemically linked via their
amino or carboxylate groups to form a peptide bond. The peptide bond is restricted in its rotation, because of its
partially double bonded character and this makes the polypeptide backbone
rather stiff [2].
Since most of the protein is
covalently bonded via single-bonds, which are freely rotatable in principle, a
number of torsional angles are commonly defined and referred to. The torsional
angles along the polypeptide chain are called omega (the peptide bond), phi
(preceeding the C-alpha atom) and psi (following the C-alpha atom). A
precise description of these angles along the protein backbone will specify the
conformation of the polypetide chain. This representation of a protein fold in
torsional space can be useful since only three parameters are required per
peptide unit, but since errors accumulate over the length of the chain, the
long-distance spatial relationships may become inaccurate [2]
.
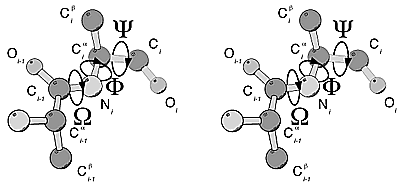
Figure 1: Stereo
view of amino acid geometry nomenclature. An alanine dipeptide is shown in an
extended conformation in which all torsional angles are at 180°. The omega
angle characterizes the peptide bond; due to it's partial double bonded nature omega
never deviates significantly from 0° (cis peptide bond) or 180° (trans peptide
bond, shown here). While there is considerable rotational freedom around the phi
and psi angles, due to steric repulsion not all torsional angles or
combinations of angles are observed in proteins.
To keep the link
simple and manageable, I used the psi angle (one following the C-alpha
atom) as the torsional angle, and treated both omega and phi as
constants. I used the C-alpha positions
as link joints, so the length of the two links was simply the distance between
two consecutive C-alpha atoms. As the
PDB file contains information about the type of atoms (“CA” for C-alpha) and
their associated position, computing the length was fairly easy. The psi angle was computed as the
rotation angle of the C-alpha vector along x-axis. All the other atoms in an amino acid were considered part of the
link. The resulting link is shown
below:
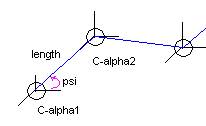
Figure 2: Molecular link approximation for the anthrax
antigen protein.
Using the Inverse Kinematics Algorithm
The molecular link
calculated in task 1 is passed to an inverse kinematics procedure [4], which calculates
the new intermediate points and angles based on initial and final
positions. I created the link tree in a
format readable by the inverse kinematics, and randomly selected one C-alpha
atom in a chain of 20 links to be the end-effector. The first C-alpha atom in the chain was used as the base
atom. The final position of the
end-effector was randomly generated.
The inverse kinematics
algorithm requires four parameters per link: length and the three euler
angles. To compute the length between
the two C-alpha atoms (C1 and C2) I used the following
equation:
L =
sqrt((x2 – x1)2 + (y2-y1)2
+ (z2-z1)2)
The three euler angles
were computed using the following equations [5], where view is the unit vector and angle is the rotation angle along x-axis for the
global co-ordinate system:
phi = arctan(view_y/view_x)
theta
= arccos(view_z)
psi = angle - phi
These three parameters
were passes on to the inverse kinematics (IK) algorithm for a set of about 20
links. The algorithm returned after
each iteration with the new normal and rotation angle (ra). These
two parameters, along with the original vector for each C-alpha atom was used
to compute the new position. The equation
that can be used for this calculation is shown below [4]:
new = cos(rotation angle)(normal)
+
(1-cos(rotation angle))(normal . original)(normal)
+ sin(rotation
angle)(normal x original)
as the rotation angle is expected to
be really small, we used an approximation to speed up the computation:
new =
normal + (rotation angle)(normal x original)
Generating PDB Files With New Data
The final task was to update parts of the PDB file to reflect the change in
each atom’s position. The updated data
can be written to a PDB file for each iteration of the IK algorithm, which can
then be converted to an IV file to be viewed in a browser.
Since the IK algorithm only used the C-alpha atom, I used the difference between
the new and previous position of each C-alpha atom in the link and updated all
other atoms in that amino acid based on this difference.
Results
I was successfully able to parse and rewrite a PDB file with the updated
data. The link information was also
generated successfully based on the above equations. However, there were probably some mathematical errors, as the end
position the computed by the IK algorithm was very different than the actual
link position.
Start Position of the end effector based on PDB data: (47.435, 44.295,
17.571)
Desired position: (91.96, 78.47, 20.65)
Position calculated by the IK algorithm after the first loop
iteration: same as the start position.
I was unable to run the IK algorithm more than once as it caused the
application to crash on the next run.
Lessons Learned
Although inverse kinematics is a very useful technique, a solution for it
in the molecular world required the molecular chain to be over simplified and
treat several parameters as constants.
For example, the anthrax antigen molecule I used has about 735
amino-acids, and if we only take the C-alpha atom for each amino acid, we still
have 734 links to iterate for each iteration of the IK algorithm. This process can be very slow and the
resulting final configuration may or may not be a valid conformation for that
molecule [1].
References
[1]
Zhang, M. and Kavraki, L. “Finding
Solutions of the Inverse Kinematics Problems in Computer-aided Drug Design”,
http://cs-tr.cs.rice.edu/Dienst/UI/2.0/Describe/ncstrl.rice_cs/TR02-385
[2] http://www.lmb.uni-muenchen.de/users/steipe/lectures/structure/node02.html
[4] http://www.cs.utexas.edu/users/bajaj/human_body_animation/human_body_animation.htm
[5] http://www.niams.nih.gov/rcn/labbranch/lsbr/software/bsoft/bsoft_orientation.html
[6] http://www.cs.utexas.edu/users/bajaj/molecular/sadia/InverseKinematics.ppt.