

The rules are quite simple, but it's actually surprisingly sophisticated. The game is known to be Turing complete. This means that any computation that can be performed could be performed by setting up an appropriate instance of the game. The most powerful computer on the planet could be simulated in the Game of Life, though it would be incredibly complicated to do so.
The universe of the Game of Life is an infinite, two-dimensional grid of cells, each of which is in one of two possible states, live or dead. Every cell interacts with its eight neighbors, which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:
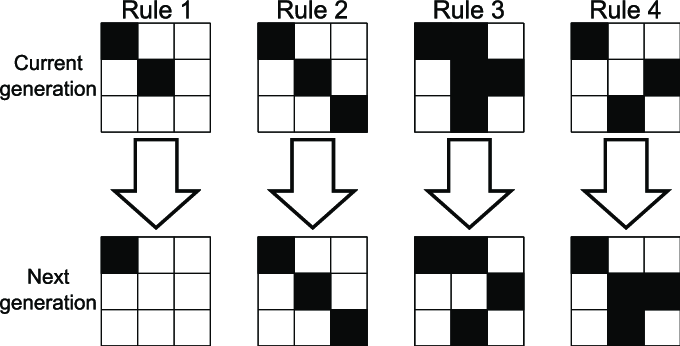
The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules simultaneously to every cell in the seed, live or dead; births and deaths occur simultaneously. The rules continue to be applied repeatedly to create further generations.
You must implement your grid as an instance of a class. Then you will write a function that updates the grid for one step according the Game of Life rules and another function that updates the grid n successive steps.
Defining the Grid Class: Each cell of the grid will contain either DEAD or LIVE. Your Grid class will have at least the methods shown in the template below. Implement your grid as a 2D list of strings where DEAD is the string "." and LIVE is the string "X". That way when you print the grid you can easily see where the cells are and see patterns of live cells. In my __str__ function, I added an extra space between cells in each row so that the grid appears more square when printed. See the sample output below.
One of the trickiest things about playing Game of Life on a finite grid is dealing with cells on the border. E.g., how many live neighbors does cell (0, 0) have? It's possible to do that by programming in a bunch of special cases. But, as with many problems in programming, there's a much easier and clever way to do it. Cells outside the grid border should be considered DEAD, but if you write your code carelessly it will crash as you try to access cells that aren't defined. My suggestion is to ask first if either or both of a cell's coordinates would make it fall outside the grid; if so, call it DEAD. Otherwise, ask if grid[row][col] contains LIVE. That way, when counting the live neighbors of cell grid[0][0] you can safely ask about the "cell" at grid[-1][-1], for example, without crashing your program. Think about this when you program the class method isCellLive.
A template for the Grid class is below. For each method, replace pass with your code.
LIVE = 'X'
DEAD = '.'
class Grid:
"""This defines the playing surface for Conway's Game of Life."""
def __init__(self, size):
"""Create the grid as a 2D list of dimensions size x size. Initially,
each cell of the grid contains DEAD."""
pass
def __str__(self):
"""Return a string to display when printing the grid.
I put in an extra space between columns so that it would
appear more square. Don't forget to include a newline
after each row."""
pass
def getGridSize(self):
"""Return the size of the grid."""
pass
def getCell(self, row, col):
"""Fetch the contents of the cell at coordinates (row, col).
Assume that these are legal coordinates."""
pass
def setCell(self, row, col, value):
"""Set the contents of the cell at coordinates (row, col) to
value (presumably this should be either DEAD or LIVE.
Assume that the coordinates are legal."""
pass
def isCellLive(self, row, col):
"""A cell is live if it's within the grid and contains LIVE.
Otherwise, it's considered DEAD. Rather than returning a
boolean, this returns 0 or 1 so we can also use this in counting
live cells. Note that in a Boolean context, 1 and 0 work just
as well as True and False."""
pass
def countLiveNeighbors( self, row, col ):
"""Count the live neighbors of the cell with coordinates (row, col).
To do this we just need to ask of each for the 8 possible neighbors
whether it's alive and count those that are. Return the count."""
pass
Other Functions: In addition to the class described above, you
must define several other functions that makes use of the class.
These are the functions that update the grid according to the rules of
the game, along with a function that makes it more convenient to set
up the initial seed. These functions should be defined outside of the
Grid class, but in the same file. Feel free to define auxiliary
functions if you like, but you must have at least the following
functions:
def makeCellsLive( grid, cellsList ):
"""Given a list of coordinate pairs (x, y), make each of these
LIVE in the grid."""
pass
def stepGameOfLife( grid ):
"""This implements one step in the Game of Life. Given a grid, update
it following the rules of the games. I.e., for each cell in the grid, count
its live neighbors and decide whether the cell is LIVE or DEAD in
the next generation. Then update the grid to reflect the changes."""
pass
def playGameOfLife( grid, n ):
"""Given an initial grid, take n steps in the Game of Life."""
pass
Notice that in stepGameOfLife you need to define another 2D
array to hold the results temporarily. You can't just modify your
input grid in place as you go. Otherwise, by the time you get to row
k you'll have already updated row k-1 which will change the results.
Instead, create an empty 2D list of the same size as your grid, put
the results there, and at the end copy them back into your grid.The coordinates of a cell are two integers row and col, where 0 ≤ row < size and 0 ≤ col < size. In function makeCellsLive the second argument is a list of coordinate pairs. Each element of this list is of the form (x, y) and you can access the components of a pair p by p[0] and p[1]. This is all explained in the Tuples material from Week 11.
The pattern shown is a "glider." In four steps the pattern repeats but has moved down and to the right.
>>> from Project2 import * >>> grid = Grid( 10 ) >>> print(grid) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> GLIDER = [ (0, 1), (1, 2), (2, 0), (2, 1), (2, 2) ] >>> makeCellsLive( grid, GLIDER ) >>> print(grid) . X . . . . . . . . . . X . . . . . . . X X X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> stepGameOfLife( grid ) >>> print(grid) . . . . . . . . . . X . X . . . . . . . . X X . . . . . . . . X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> stepGameOfLife( grid ) >>> stepGameOfLife( grid ) >>> stepGameOfLife( grid ) >>> print(grid) # glider again, but moved . . . . . . . . . . . . X . . . . . . . . . . X . . . . . . . X X X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> playGameOfLife( grid, 4 ) >>> print(grid) . . . . . . . . . . . . . . . . . . . . . . . X . . . . . . . . . . X . . . . . . . X X X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>>
Another interesting pattern is the "pentadecathlon." It goes through 14 different patterns before it repeats. Note: it's necessary to build it away from the borders because some of the intermediate patterns are larger than the initial pattern.
> python Python 3.8.10 (default, Jul 29 2024, 17:02:10) [GCC 9.4.0] on linux Type "help", "copyright", "credits" or "license" for more information. >>> from Project2 import * >>> grid = Grid( 20 ) >>> print(grid) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> PENTADECATHLON = [ (5, 5), (5, 6), (4, 7), (6, 7), (5, 8), (5, 9), (5, 10), (5, 11), (4, 12), (6, 12), (5, 13), (5, 14) ] >>> makeCellsLive( grid, PENTADECATHLON ) >>> print(grid) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . X . . . . X . . . . . . . . . . . . X X . X X X X . X X . . . . . . . . . . . . X . . . . X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> stepGameOfLife( grid ) >>> print( grid ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . X X X X X X X X . . . . . . . . . . . . X . X X X X . X . . . . . . . . . . . . X X X X X X X X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> stepGameOfLife( grid ) >>> print( grid ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . X X X X X X . . . . . . . . . . . . . X . . . . . . X . . . . . . . . . . . X . . . . . . . . X . . . . . . . . . . . X . . . . . . X . . . . . . . . . . . . . X X X X X X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>> playGameOfLife( grid, 13 ) >>> print( grid ) # back where we started . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . X . . . . X . . . . . . . . . . . . X X . X X X X . X X . . . . . . . . . . . . X . . . . X . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . >>>You should try some of your own patterns. If you Google "Conway's Game of Life" you can find some interesting ones. Some repeat (after a certain period), some move across the grid, some disappear, some grow, etc. The TAs should be able to import your module and run their your own patterns to see that your functions work correctly. Here are some patterns you can explore:
BLINKER = [ (3, 3), (4, 3), (5, 3) ]
BLOCK3x3 = [(3, 3), (3, 4), (3, 5), (4, 3), (4, 4), (4, 5), (5, 3), (5, 4), (5, 5)]
BLOCK2x4 = [(3, 3), (3, 4), (3, 5), (3, 6), (4, 3), (4, 4), (4, 5), (4, 6)]
CROSS = [(7, 3), (7, 4), (7, 5), (7, 6), (7, 7), (7, 8),
(8, 3), (8, 4), (8, 5), (8, 6), (8, 7), (8, 8),
(5, 5), (5, 6), (6, 5), (6, 6), (9, 5), (9, 6), (10, 5), (10, 6)]
Your file must compile and run before submission. It must also contain a header with the following format:
# Assignment: Project2 # File: Project2.py # Student: # UT EID: # Course Name: CS303E # # Date: # Description of Program:
