A position paper for the FMWG

Lesley Semmens, Leeds Metropolitan University, UK

L.Semmens@lmu.ac.uk

This is just a sketch of what I do – I am happy to answer any questions from members of the WG over the next few days. I will begin by outlining the approach I take to teaching formal methods, and then discuss briefly the reasons for using this approach. I have included some examples of material I use with my students.

Here at LMU I take an integrated approach to the teaching of Z to the second and final year students on the Software Engineering route of our BSc Computing degree. The students have already studied discrete maths and logic in a first year, mathematically based module which includes a brief introduction to Z schema notation.

I teach the second year System Specification module which aims to get the students to a point where they can:

1. explain the importance of requirements analysis and specification in the development of systems

 

2. read and explain requirements specification documents written using a range of techniques and notations

 

3. demonstrate a proper understanding of the mathematical foundations of formal methods.

 

4. given a written description of a system, produce an accurate and complete formal specification (we use Z)

 

5. critically appraise the contribution of formal specification to software production.

In the final year the students study Advanced Software Engineering which includes learning outcomes that the students should:

• consolidate a range of techniques and skills from across the course of study which impinge upon software development

• understand the need for integration of different methods for software development.

Throughout my teaching in the second and final years I try to relate Z to other notations, with which the students are familiar, so that they see Z as just another notation for specifying systems, rather than something alien that does not relate to other things they cover.

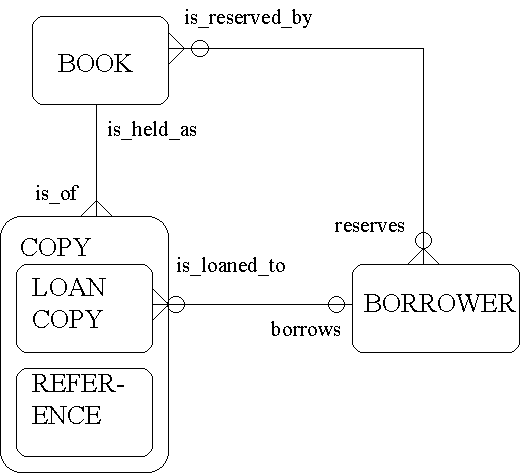
I start, with the second year students, by relating the Z state schema to an Entity Relationship Diagram (see the Library example below).

In the final year Advanced Software Engineering module we look more at the theory of Methods Integration. I also look at how other notations, e.g. state-transition diagrams, can help in developing other parts of the specification e.g. preconditions for operations. We also look at how we might add more detail, such as that included in Entity Attributes (see the last parts of the Library example below).

I see the main problem in the early teaching of formal methods to be the students’ limited ability to model. The notations are not the main problem. I therefore try to build on other experience and understanding they already have. I have tried many different approaches over the ten years I have been teaching formal methods. I have done it with and without tools (fUZZ, Formaliser, ZTC). We have even built tools to translate from ERDs to Z. But, always it comes back to the students’ ability (or lack of ability) in modelling. Using tools student beginners produce syntactically correct Z, but often it is semantic nonsense; they concentrate far too much on the syntax and coping with the ideosyncracies of the tool.

I am not totally against tools. With the final year, who have more understanding of what they are doing (and more ability in modelling), I use tools, such as fUZZ and ZTC if time permits. In any case I encourage them to try out the tools, in the same way as they might any other software engineering tool. This seems to work, they are not trying to learn two things at once and appreciate the help the tool gives them.

NB

I have not included references. I know Neville is aware of my Methods Integration work, and I have had a number of papers at computing education conferences. If anyone wants references to the education work and/or the methods integration stuff please contact me.

1. The system allows the acquisition of books, of which multiple copies may be held.

 

2. Borrowers may register with the library.

 

3. Copies may be borrowed by registered borrowers who may also return them.

 

4. There is a predefined limit on the number of copies each user may borrow.

 

5. Copies may be for reference only or for loan.

 

6. If there are no copies of a book on the shelves then the book may be reserved by a borrower.

 

7. A user should be able to make enquiries for books by a particular author or on a particular subject.

Introduce a basic type for each entity:

[BOOK, COPY, BORROWER]

We have a requirement that there be a limit on the number of copies each user may borrow so we need to introduce a constant MaxLoans.

MaxLoans : N

Books : P BOOK

Copies : P COPY

LoanCopies : P COPY

Reference: P COPY

Borrowers : P BORROWER

Copy_isof_Book : COPY ß BOOK

Book_isreservedby_Borr : BOOK « BORROWER

Copy_isloanedto_Borr : COPY ß BORROWER

á LoanCopies, Referenceñ partition Copies

dom Copy_isof_Book = Copies

ran Copy_isof_Book = Books

dom Book_isreservedby_Borr Í Books

ran Book_isreservedby_Borr Í Borrowers

dom Copy_isloanedto_Borr Í LoanCopies

ran Copy_isloanedto_Borr Í Borrowers

A b : ran Copy_isloanedto_Borr ·

# (Copy_isloanedto_Borr t {b}) £ MaxLoans

An initial list of candidate events might be as follows:

E1 Borrower joins library

E2 Borrower leaves library

E3 Borrower reserves book

E4 Borrower requests loan

E5 Borrower returns copy

E6 New book acquired by library

Checking the model, using a CRUD (Create, Read, Update, Delete) matrix, to help identify missing events

CRUD matrix for the library system

COPY is never deleted.

The additional required event is:

E7 Copy removed

Revised CRUD matrix

Extract from Loan Copy entity life history

Loan copies may either be on the shelf or on loan, so we can partition the set of copies further and also refine the constraint on dom Copy_isloanedto_Borr.

The improved specification is now:

Books : P BOOK

Copies : P COPY

OnShelf : P COPY

OnLoan: P COPY

Reference: P COPY

Borrowers : P BORROWER

Copy_isof_Book : COPY ß BOOK

Borr_reserves_Book : BORROWER j BOOK

Copy_isloanedto_Borr : COPY ß BORROWER

..... schema continues .....

á OnShelf, OnLoan, Reference ñ partition Copies

dom Copy_isof_Book = Copies

ran Copy_isof_Book = Books

dom Borr_reserves_Book Í Borrowers

ran Borr_reserves_Book Í Books

dom Copy_isloanedto_Borr = OnLoan

ran Copy_isloanedto_Borr Í Borrowers

" b : ran Copy_isloanedto_Borr ·

# (Copy_isloanedto_Borr t {b}) £ MaxLoans

We can begin to specify the IssueCopy operation if we first draw a mini-DFD.

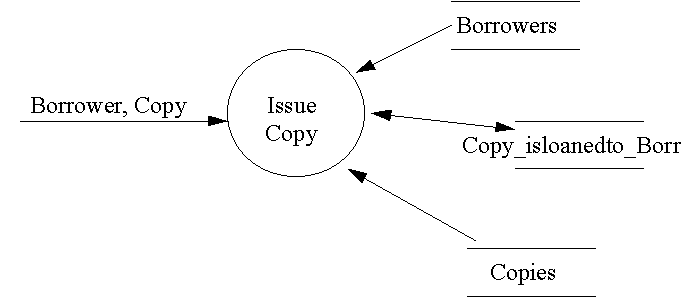
From the DFD and the Entity Life History we can extract some preconditions on the operation:

Library2

copyID? : COPY

borrowerID? : BORROWER

copyID? e OnShelf

borrowerID? e Borrowers

#(Copy_isloanedto_Borr t {borrowerID?}) < MaxLoans

The operation can then be completed by adding the values of the state variables after the operation:

D Library2

copyID? : COPY

borrowerID? : BORROWER

copyID? e OnShelf

borrowerID? e Borrowers

#(Copy_isloanedto_Borr t {borrowerID?}) < MaxLoans

Copy_isloanedto_Borr' = Copy_isloanedto_Borr U

{copyID? a borrowerID?}

OnShelf' = OnShelf \ {copyID?}

OnLoan' = OnLoan U {copyID?}

Reference' = Reference

Borrowers' = Borrowers

Copy_isof_Book' = Copy_isof_Book

Borr_reserves_Book' = Borr_reserves_Book

We now consider what would be needed to cover requirement 7, the need to be able to list books by an author or on a particular subject:

BookDetails ::= Book + Title + Subject + Author

We need some more basic types:

[TITLE, SUBJECT, AUTHOR]

Book : BOOK

Title : TITLE

Subject : SUBJECT

Author : AUTHOR

The book details can be added using an injection BookId from BOOK to BookDetails the value of this injection is constrained in the predicate.

BookId : BOOK © BookDetails

Copies : P COPY

OnShelf : P COPY

OnLoan: P COPY

Reference: P COPY

Borrowers : P BORROWER

Copy_isof_Book : COPY ß BOOK

Borr_reserves_Book : BORROWER j BOOK

Copy_isloanedto_Borr : COPY ß BORROWER

BookId = {b:BookDetails | b.Book Î Books · b.Book a b }

á OnShelf, OnLoan, Reference ñ partition Copies

dom Copy_isof_Book = Copies

ran Copy_isof_Book = Books

dom Borr_reserves_Book Í Borrowers

ran Borr_reserves_Book Í Books

dom Copy_isloanedto_Borr = OnLoan

ran Copy_isloanedto_Borr Í Borrowers

" b : ran Copy_isloanedto_Borr ·

# (Copy_isloanedto_Borr t {b}) £ MaxLoans

Now an enquiry operation to list books on a particular subject can be specified

X Library3

subject? : SUBJECT

books! : P BookDetails

books! = { bd : ran BookId | bd.Subject = subject? }