Chapter 4: Introduction to DAGH

Conceptual Overview of DAGH

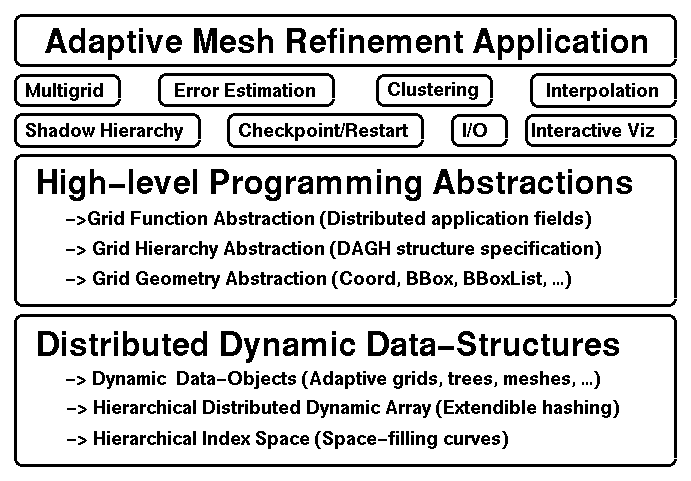
DAGH provides a program development infrastructure for implementation of solutions of partial differential equations using adaptive mesh refinement algorithms. The principles of hierarchical abstraction and separation of concerns were incorporated into the development of DAGH.

Figure 2: Design model for DAGH

Figure 2 is a schematic design model for DAGH. Each level can be thought of as a set of abstract data types. The lowest level defines a hierarchical dynamic distributed array (HDDA) that is a generalization of the familiar static array. It has the operations of creation, deletion, array expansion and contraction, and array element access defined on it.

We illustrate the separation of concerns by defining a separate level (above HDDA) to implement grids and/or meshes. This abstraction level implements grids by instantiating arrays as components of grids. In the definition of grids are the operations of creation, deletion, expansion, and contraction. These operations are directly translated to operations on instances of HDDA. The definition of grids also includes computational operators, partitioning operators, refinement and coarsening operators, etc.

Figure 3: DAGH Abstraction Hierarchy

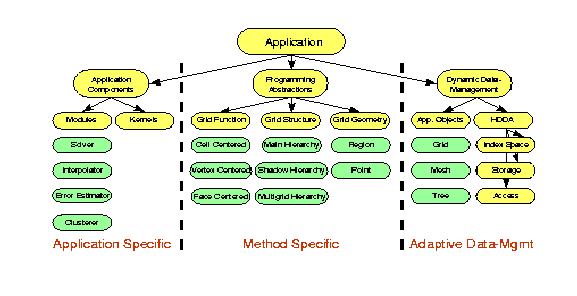
Figure 3 is another schematic diagram of the levels of abstraction in DAGH. But in this figure the hierarchy descends from left to right. Each level of the hierarchy is given in more detail from top to bottom.

An application consists of specific components. These components are mapped to operations on appropriate subtypes on their right in the programming abstraction layer. The grid subtypes are mapped to the types implemented by the dynamic data management layers to their right.

The Grid Structure abstractions define hierarchical grids and implement standard operations on these grids. These abstractions represent the structure of the geometry of the computational domain. The Grid Function abstractions define application fields on the Grid Structure. These abstractions define the data storage associated with a grid structure. This separation of Grid Function from Grid Hierarchy enables the structure of the computational domain to be defined and manipulated independent of the computational data.

The Grid Geometry abstractions represent regions in grid space that are independent of grid type. These abstractions provide the means for interacting with grids and addressing and directing computations to regions on the grids.

DAGH Data Structures

Hierarchical Dynamic Distributed Array (HDDA) is the data structure abstraction used in DAGH. HDDA is an array data type that has the operations of creation, deletion, array expansion and contraction, and array element access and storage defined on it. Separation of concerns applies vertically within the definition of HDDA. HDDA is composed of three abstractions: index spaces, storage, and access.

Index Space

The index space is a lattice of points in an n-dimensional discrete space. It is recursively defined so that each position in an index space could be an index space.

Storage

This is a mapping from the n-dimensional index space to a one dimensional physical storage. Space filling curves [Hans Sagan, Space-Filling Curves, Springer-Verlag, 1994] allow mappings from a multi-dimensional space to a 1-dimensional space. Thus given an index in the 1-dimensional space one can find its position in the multi-dimensional space.

Access

This is a set of operations for returning the values associated with positions in the index space from the associated storage.

Data storage is implemented using extendible hashing techniques to provide a dynamically extendible, globally indexed storage. Entries in the HDDA correspond to DAGH blocks. Each block in the list is assigned a cost corresponding to its computational load. The grid hierarchy can be partitioned by appropriately partitioning the linear representation of a DAGH instance across processors so as to balance the computational cost associated with each processor.

Structure of DAGH-based code

DAGH provides the class libraries needed to implement adaptive mesh refinement methods and to run a program on parallel processors. All programs that use DAGH have a common structure. This structure can be viewed as a template for application dependent routines which are supplied by the user. To create a DAGH-based application you have to provide -

• Driver
  The driver creates and initializes the DAGH hierarchy, sequences invocations of the solution operations, and interfaces to visualization routines. A detailed discussion of the structure of the driver is given next section.
• Routines to perform grid level operations
  Update functions for
  • Interior points
  • Boundary points
  To update the values of the function at the grid points both inside the region under consideration as well as on the boundary the user supplies the kernels. The kernels can be written in Fortran 77, Fortran 90, C, or C++. It is important to remember that DAGH uses storage maintained in Fortran compatible fashion.
• Routines to perform inter-grid level operations
  • Prolongation
  • Restriction
• Several utility operations
  • I/O routines
  • Visualizations interface
  • Clustering routines
    DAGH provides the I/O framework. The input parameters can be hard coded into the driver or if the DAGH I/O routine is initialized then the input parameters can be read from a file. The output is sent to an IO server. How the output is then written to a file or sent to a visualization interface is defined by the user.
• Routine to perform error estimates
• Input parameter file (optional)
• Makefile

Driver

The driver is a C or C++ program (although drivers can be written in Fortran this option is not discussed in the tutorial). The driver needs to be compiled. One usually uses a makefile to do the compilation. After compilation you can run the executable code on a single processor or use MPI to run it on several processors. The top level view of the structure of the driver is as follows:

• Initialize the environment
  • MPI (Message Passing Interface)
  • I/O
  • Graphical Interface
  • Open files
  • Steering (change values of variables during the computational process)
  • Interaction (check point, roll back, restart)
• Read the input parameters for the problem
  • dimension of the grid
  • size of the grid
  • grid step
  • lower and upper bounds for each of the coordinate directions
  • time step
• Setup Grid structure
• Setup Grid functions
• Setup initial conditions
• Start the Main Loop
  • User interaction or control
  • Update grid functions at
    • Interior
    • Boundary
  • Communicate result of updating with other grids
  • Output result to a file and / or output to a visualization interface
• End Main Loop
• Shutdown environment
  • MPI
  • I/O
  • Graphical Interface
  • Files

The DAGH Interface

The DAGH interface includes:

• creation and deletion of instances of DAGH's
• definition of logical regions within the DAGH hierarchy (a logical region region that includes a span of the grid hierarchy)
• applications of user defined operations to the logical regions of the grid hierachy

An instance of DAGH typically includes:

• a main grid hierarchy to which the operations are applied
• a shadow hierarchy which is used to store past states of the DAGH for use in error estimations