Your assignment is to write a program that will determine, given a sample of sound from a piano key, what key (1-88) and note (A-G#) it is.

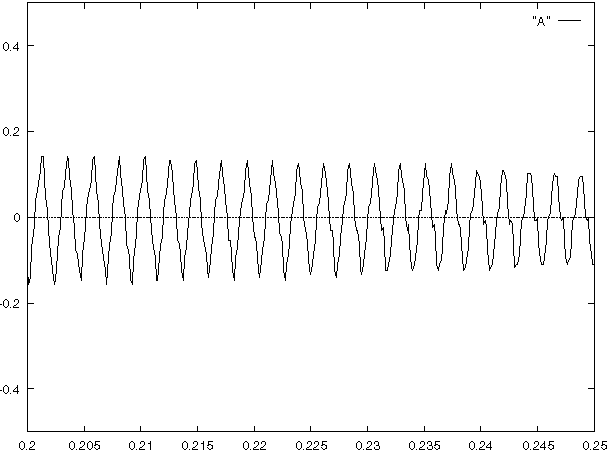
The x axis is the number of seconds from the time the key was
struck; as
you can see, we are considering only 1/20 of a second of time.
This piano key happens to be the A above middle C, tuned at 440 Hertz
(abbreviated Hz). That means the string vibrates 440 times per second.
The y axis plots the amplitude of the compression of air around a
microphone
connected to my computer; you can think of it as a voltage level.
As you can see from the plot, the voltage level, or signal, spikes
once every 1/440 of a second.
Sound is a continous signal, so how do we reprent it inside the computer?
One way is to take a sample of the amplitude of
the signal once every, say, 1/8000 of a second. We can store
these samples in a large array. Whenever we want to look at the signal
at time t, where t is in seconds, we just multiply
t by 8000,
find the closest integer, and look in the array at that point. In fact,
this is exactly the way sound is stored on an ordinary CD, with samples
taken every 1/44000 of a second.
How do you determine the frequency of a sampled sound? This situation
is complicated by the fact that in most situations, including the piano
key strike, there are many frequencies superimposed on each other. For
example, the A above also vibrates at 880 Hz, 1320 Hz, and other frequencies,
although these show up at a lower amplitude. These harmonic
frequencies are what give the piano,
other instruments, your voice, and pretty much every other sound its
characteristic texture. However, we are now only interested in determining
the fundamental frequency.
The data are given to us in the time domain, i.e., we know, for any
given time, what the amplitude will be. It would be nicer if the data
were in the frequency domain, where we would know, for any given
frequency, what the amplitude will be. Then we can just look for the
frequency with the highest amplitude, and that's the fundamental frequency
(usually; it works for the middle part of the piano, at least).
The Fourier Transform of a function takes a function y(t)
in the time domain and ``transforms'' it into a function Y(f) in the
frequency domain. It works for any periodic continuous function.
The Fourier Transform, for your amusement, looks like this:
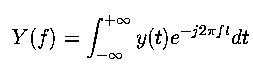
If you don't know what this means, don't worry; you don't have to.
cfft (complex_array, 8192)
where complex_array is the name of your array.
Your time-domain data will be replaced with the frequency domain data
from the Fourier transform. Copy cfft.o and cfft.h
to your directory. Call
your program file piano.c and write a Makefile for it;
remember to link the file cfft.o with a line like:
$(CC) -o piano piano.c cfft.o -lmin your Makefile. You may also wish to use the complex array routines discussed in class; they are available as complex.c and complex.h on this web site. I have done so for my program; my Makefile looks something like this:
CFLAGS = -g -Wall
LDLIBS = -lm
CC = gcc
all: piano
piano: piano.o cfft.o complex.o
$(CC) -o piano piano.o complex.o cfft.o $(LDLIBS)
piano.o: piano.c cfft.h complex.h
complex.o: complex.h complex.c
You should do all your work in a subdirectory called assign5.
The output of your program should be give the maximum
amplitude, the fundamental frequency, the key number, and the symbol
for the note. So, your program should:
runner% piano 1.dat maximum amplitude is 55.04 at 155.27 Hz, key = 31 key letter is D# runner% piano 2.dat maximum amplitude is 33.75 at 330.08 Hz, key = 44 key letter is E runner% piano 3.dat maximum amplitude is 143.59 at 310.55 Hz, key = 43 key letter is D#To turn in this program, do exactly this from the prompt on runner, after having compiled your program:
% cat piano.c > output % piano ~djimenez/cs1713/1.dat >> output % piano ~djimenez/cs1713/2.dat >> output % piano ~djimenez/cs1713/3.dat >> output % piano ~djimenez/cs1713/4.dat >> output % piano ~djimenez/cs1713/5.dat >> output % piano ~djimenez/cs1713/6.dat >> output % piano ~djimenez/cs1713/7.dat >> output % piano ~djimenez/cs1713/8.dat >> output % piano ~djimenez/cs1713/9.dat >> output % piano ~djimenez/cs1713/10.dat >> output % Mail -s "piano program" djimenez@ringer.cs.utsa.edu < outputThis will run your program on all the files and send me the output. (If you have written other files beside piano.c, e-mail me them, too, separately.) Expect the run time of this program to be rather long, on the order of a few seconds; an FFT is a computationally expensive operation, especially when there are 30 other students on runner running the same program.