Consider a weighted, directed graph
G = (V, E, w).
V is the set of vertices.
E is the set of edges that are order pairs linking the vertices.
w is a function from E to the real numbers
giving the weight of an edge.
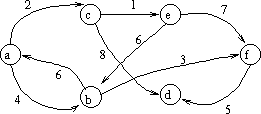
For example, in the following graph:

A path through the graph is a sequence of vertices that are connected by edges. For instance, (a, b, f, d) is a path connecting vertex a to vertex d. The length or cost of a path is the sum of all the weights of the edges traversed. The length of (a, b, f, d) is w(a, b) + w(b, f) + w(f, d) = 4 + 3 + 5 = 12. Another path is (a, c, d), with length 2 + 8 = 10, so some paths are longer than other.
We would like to know, given a single source vertex, what the length of the shortest path to any other vertex is. This is the single-source shortest paths problem. It can be solved with a greedy algorithm called Dÿkstra's Algorithm.
In the algorithm, we will arrange V as an sequence from 1..n, with vertex #1 being the source vertex. We'll have an array D[2..n] keeping track of the current minimum distances; at any point in the algorithm, D[i] is the current minimum length of a path from vertex #1 to vertex #i. There is a priority queue Q that contains vertices whose priorities are their values in D (smaller value means higher priority). Note that the priority queue must be able to automatically account for adjustments to D, so we'll have to use something a little more sophisticated than a heap (but just a little).
Dÿkstra (G, s) n = the size of V for i in 2..n do // initially, D[i] is the weight D[i] = w (1, i) // of the edge from vertex 1 to i, end for // which might be infinite for all i >= 2 in V, insert i into Q, using D[i] as the priority repeat n-2 times v = Extract-Minimum (Q) // v is the closest vertex to #1 for each vertex w left in Q do D[w] = min (D[w], D[v] + w (v, w)) end for end repeat return DD starts out as the obvious first guess: the length of the edge from 1 to i for i in 2..n. This might not be the best guess, especially if there is no edge and the w function returns infinity. Q starts with all the vertices in it.
In a loop, we greedily go toward the vertex v closest to 1, the minimum element in the queue. At this point, we know the length of the minimum path from 1 to v that doesn't go through any of the vertices in Q. We then update D, offering each other vertex w a possibly shorter path length from vertex 1 via v, i.e., path from 1 --> v --> w. If the length in D is greater than this length, we replace it.
At the end of the algorithm, all vertices but the farthest one from 1 have been removed from the queue, thus D has the lengths of the shortest paths through any vertex.
Let's use the above graph for an example of Dÿkstra's Algorithm starting from vertex a:
Initially:
Q = { b, c, d, e, f} (think of them as 2..5)
b c d e f
D[2..5] = [ 4 2 oo oo oo ]
repeat loop starts:
minimum v from Q = c, with D[c] = 2. Now Q = { b, d, e, f }.
Look at path lengths from a through c to { b, d, e, f }
D[b] = 4, D[c] + w (c, b) = oo, no change.
D[d] = oo, D[c] + w (c, d) = 8, so now D[d] = 8 (a->c->d)
D[e] = oo, D[c] + w (c, e) = 3, so now D[e] = 3 (a->c->e)
D[f] = oo, D[c] + w (c, f) = oo, no change
b c d e f
Now D = [ 4 2 8 3 oo ]
minimum v from Q = e, with D[e] = 3. Now Q = { b, d, f }
Look at path lengths from a through e to {b, d, f}
D[b] = 4, D[e] + w (e, b) = 9, so no change.
D[d] = 8, D[e] + w (e, d) = oo, so no change
D[f] = oo, D[e] + w (e, f) = 10, D[f] = 10 (a->c->e->f)
b c d e f
Now D = [ 4 2 8 3 10 ]
minimum v from Q = b, with D[b] = 4. Now Q = { d, f }
Look at path lengths from a through b to {d, f}
D[d] = 8, D[b] + w (b, d) = oo, so no change.
D[f] = 10, D[b] + w (b, f) = 7, so D[f] = 9 (a->b->f)
b c d e f
Now D = [ 4 2 8 3 9 ]
minimum v from Q = d, with D[d] = 8. Now Q = { f }
Look at path length from a through b to f
D[f] = 9, D[d] + w (d, f) = oo, so no change.
We are done; f is the only element of the queue, so it can't help make
any other path lengths shorter.
b c d e f
D = [ 4 2 8 3 9 ]
If we assume an
adjacency matrix representation, then w is just an O(1)
array access and Q is a queue of array indices. Storage
for an adjacency matrix is
If we want to use a heap-based priority queue, we'll have to call
Heapify each time D is updated, which happens
O(|Q|) times throughout the repeat loop
and takes O(ln |Q|) time for each call.
The initialization of D is
The repeat loop happens n-2 times. Let e = |E|,
i.e., the number of edges. No edge is considered more than once in the
for each edge loop, so this is an upper bound on the number of
possible updates to D and thus calls to Heapify, which
each cost O(ln n) time. We must
do an Extract-Minimum each time through the repeat
loop, each of which also cost O(ln n) time. So we
the algorithm runs in time O(n ln n) (for
initializing the queue) + O(n ln n) (for
the calls to Extract-Minimum) + O(e ln n)
(for all the calls to Heapify when we update D),
= max (O(n ln n),
O(e ln n)).
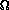 (n2).
If we know that there are very few edges, an adjacency list representation
would be more appropriate. We'll assume a matrix representation for the
analysis.
(n2).
If we know that there are very few edges, an adjacency list representation
would be more appropriate. We'll assume a matrix representation for the
analysis.
 (n), the
initialization of the queue is O(n ln n)
(n inserts into a heap, each costing O(ln n) time).
(n), the
initialization of the queue is O(n ln n)
(n inserts into a heap, each costing O(ln n) time).