Lecture 6

Heapsort continued

Building a Heap

We would like to take an unordered array of items and make it into a heap. Basically, we want each node to satisfy the heap property, i.e., each node's value should be at least that of its children. We'll do this with two procedures:

Heapify(A,i) will make a subheap out of the ith element of the array, provided that Left(i) and Right(i) are both heaps:

Heapify (A, i)
        l = Left (i)			// 'largest' will be the index
        r = Right (i)			// of the largest of nodes 'l',
 					// 'r', and 'i'
 
        if (l <= heap_size(A) and A[l] > A[i]) 
                largest = l
        else
                largest = i
        if (r <= heap_size(A) and A[r] > A[largest])
                largest = r
 
        if (largest != i)		// 'i' should be the largest.
					// if it isn't, then swap it
					// with the largest child
                exchange A[i] with A[largest]
					// the exchange may have violated
					// the heap propery, e.g.:
                        5               7
                      /   \           /   \
                     4     7  ===>   4     5    <--- this subheap is
                    / \   / \       / \   / \        no longer a heap!
                   1  2  3   6     1  2  3   6
			                // so we must re-establish the 
					// heap property, possibly marching 
                Heapify (A, largest)	// down a path of the tree 
					// recursively swapping
					// things into place.

Build-Heap(A) will start at the last node of the array that could possibly have children, i.e., could possibly violate the heap property, and swap elements such that the node satisfies the heap property and is the root of a subheap. It will continue doing this node by node until it reaches the root:
```
Build-Heap (A)
	heap-size(A) = length(A)	// the heap is same size as the array
	for i in floor(n/2) downto 1 do	
		Heapify (A, i)		// Heapify each non-leaf node
	end for
```

Now for the analysis. How long does Heapify take? We can count array accesses or machine instructions, but they are all pretty much proportional to one another. There are no loops, so Heapify takes

(1) time for each recursive call. So the question is, how many recursive calls will Heapify do? In the best case, it won't do any, so the answer is

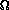(1). We're more interested in the worst case. In this case, Heapify traces a path from the root node down possibly to the parent of a leaf node, swapping elements each time. If the tree has a height of h, then Heapify can't call itself recursively more than h times, since any path from root to parent of a leaf is at most of length h. So Heapify runs in time O(h). Recall that there are at most n=2^h+1-1 nodes in an almost complete binary tree of height h, so Heapify runs in time O(ln n).

How long does Build-Heap take? Clearly, it calls Heapify n/2 times, so it takes O(n h) = O(n ln n). But this isn't the whole story; O(h) is an upper bound for Heapify. Most calls to Heapify are done on nodes that are the roots of subtrees far smaller than size n. For example, a node at level 4 will have only n/16 descendants under it. The larger i is in Heapify, the farther down in the tree i occurs, and thus the fewer nodes Heapify has to consider.

We'll start by counting the number of nodes at depth d in the tree, and figuring out how much time Heapify must spend on each one. We know that a complete binary tree of height d has 2^d+1-1 nodes. If we subtract off all the nodes at levels lower than d (i.e., the number of nodes in a tree of height d-1), we get 2^d+1-1 - (2^d-1) = 2^d nodes at level d. The heights of each subheap of these nodes is h-d, so at level d Heapify only has to do O(h-d) work.

Now if we count the amount of work done for all levels, i.e. from level 0 to level h, we get big-oh of:

h
(h-d) 2^d d=0

which works out to:

h
- [d 2^d] + h(2^h+1-1
) d=0

Amazingly, through the magic of guesswork and a gross proof by induction you don't want to see, it turns out that:

h
[d 2^d] = [(h-1) 2^h+1+2]
d=0

So we can rewrite our equation, after some simple algebraic manipulations, as

2^h+1- h - 2.

But wait! That looks familiar; it is a little less than the number of nodes in our heap, i.e., n-1-h. So the time for Build-Heap is just O(n). Since in the best case, Heapify will have to do O(1) work and still be called n/2 times, Build-Heap will take

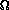(n) time, so

(n) is a tight bound for Heapify.

Now let's look at the Heapsort algorithm itself. It takes the root of the tree, which we know must be the largest element in the array, and swaps it with the last element in the array; now the largest element is in the right place. The size of the heap is reduced by one, then Heapify is done to correct the damage done by putting a small element in the root's place. This process continues until the entire array has been processed and the very smallest element is swapped up to the top of the array. It's kind of like the selection sort algorithm in reverse, only Heapsort has a O(1) way of finding the maximum element in the array! Here it is:

Heapsort (A)
	Build-Heap (A)
	for i in length(A) downto 2 do	// no need to make a singleton heap
		exchange A[1] with A[i]	// put the biggest element into
					// its place at decreasing spots in A
		heap-size(A)--		// decrease the size of the heap by 1
		Heapify (A, 1)		// reinstate the heap property
	end for

The call to Build-Heap takes time

(n), then we do n-1 swaps and decrements (each of constant time) and calls to Heapify, each of time O(ln n). So the whole thing takes

(n) + O(n ln n) = O(n ln n).