Consider the problem of sorting and array A[1..n]
of unique positive integers. That is, we are guaranteed there are no duplicates.
Professor Fubar claims that there is a worst-case lower bound of
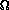 (n ln n) on
the number of array accesses needed to solve this problem.
(n ln n) on
the number of array accesses needed to solve this problem.
We know that this is true for a comparison sort, but it's not
clear whether this extends to every sorting algorithm.
Professor Emacs refutes the claim with this argument: Arrange the
integers as a list of strings of digits, using leading zeros when needed,
then use radix sort. We know radix sort makes
 (c n)
array accesses where c is the number of digits per item.
If c is a constant, then only
(c n)
array accesses where c is the number of digits per item.
If c is a constant, then only
 (n) array accesses are needed.
(n) array accesses are needed.
Is this a valid refutation of the claim? Explain your answer in
two or three brief sentences. Remember, we interested only in this
refutation, so don't try to think of a different algorithm.
No. Since the integers are all unique, we know that at least one of them
must be greater than n (if they were all less than n, then there would
have to be duplicates). So a lower bound on the value of c for radix sort
is the number of digits in n, i.e., floor(1 + log10 n). So radix sort would
take 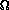 (n log10 n) =
(n log10 n) = 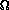 (n ln n) time, which is what Professor Fubar predicted.
(n ln n) time, which is what Professor Fubar predicted.
Consider the following recursive algorithm for sorting a subarray
A[i..n] of unique items.
It it initially invoked as Sort (A, 1, n) to sort the entire
array. It returns a truth value that is True if the array is sorted,
False otherwise; this value is only used in the algorithm for deciding
whether to continue sorting.
1 Sort (A, i, n)
2 if i = n then
3 for j in 2..n do
4 if A[j-1] > A[j] then return False
5 end for
6 return True
7 else
8 for j in i..n do
9 exchange A[i] with A[j]
10 if Sort (A, i+1, n) then return 1
11 exchange A[i] with A[j]
12 end for
13 return False
14 end if
Note that the value of i recursively increases from 1 to n
(see line 10). The recursion stops when i reaches n; at
this point, the array is checked to see if it is in order. If it isn't,
False is returned and the algorithm continues. If it is, True is returned
and all the recursion "unwinds" and stops, leaving the array in
sorted order. The when i isn't equal to n, the
algorithm tries exchanging every element in
A[i..n] with A[i], seeing
if the resulting array is (recursively) sorted (and if so, returning
with True), then restoring the array to its original order to try again.
This just generates every possible permutation of A[1..n],
testing each one to see if it is sorted.
Give upper and lower bounds on the number of times line 4 is
executed. Your bounds should be within a factor of n
of each other. You may assume that, on average, half of the permutations
must be checked before the sorted one is found.
Line 4 is part of the loop that checks whether the array is sorted. It is
executed at least once every time the loop is reached. Since the algorithm
simply goes through all possible permutations of the array, line 4 is executed
at least 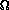 (n!) times (exactly 1/2 n! times if we find the sorted
permutation halfway through the set of permutations).
(n!) times (exactly 1/2 n! times if we find the sorted
permutation halfway through the set of permutations).
Since line 4 is in a loop that might not end until n comparisons have been
done, and the "for" loop is done 1/2 n! times, an upper bound is O(n n!), or
O(n2 (n-1)!).
[ Note that this is a mind-numbingly inefficient algorithm! Note also that
finding the right answer quickly is just a matter of what to ignore in
the text of the problem. Lines 7 through 14 of the algorithm, an opaque
jumble of recursive invokations, can be ignored since the problem itself
states that "this just generates every possible permutation" of the
array, and we know that there are n! permutations of n things.]
 (2n)
(2n)
 (n2)
(n2)
 (2n+4)
(2n+4)
 (logb n), for a and b constant, a!=b
(logb n), for a and b constant, a!=b
 (nb), for a and b constant, a!=b
(nb), for a and b constant, a!=b
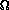 (ln n) time.
(ln n) time.