

O is an upper bound. To say that something has an upper bound of "at least" x means it could be less than x or it could be more than x. It's like if you ask someone "Do you know the upper bound" and the response is "Maybe I do and maybe I don't."
Exercise 2.1-4.
2n+1 = O(2n) because 2n+1 = 2 * 2n = O(2n).Suppose 22n = O(2n) Then there exists a constant c such that for n beyond some n0, 22n <= c 2n. Dividing both sides by 2n, we get 2n < c. There's no values for c and n0 that can make this true, so the hypothesis is false and 22n != O(2n).
| A | B | O | o | 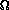 |
w |  |
|---|---|---|---|---|---|---|
| lgk n | n |
yes | yes | no | no | no |
| nk | cn | yes | yes | no | no | no |
| n1/2 | nsin n | no | no | no | no | no |
| 2n | 2n/2 | no | no | yes | yes | no |
| nlg m | mlg n | yes | no | yes | no | yes |
| lg n! | lg nn | yes | no | yes | no | yes |
Problem 2-3.
We are to rank the functions given in order of increasing asymptotic growth. Here is my ranking. Functions on the same line are in the same equivalence class, i.e., theta of each other. If you get most of them in the right order, you'll get full credit.
1, n1/lgn
lg*(lg n)
lg(lg* n)
lg *n
ln ln n
sqrt(lg n)
ln n, 2lg* n
lg2n, (lg n)!
(lg n)lg n
sqrt(2)lg n
2sqrt(2 lg n)
n, 2lg n
n lg n, lg (n!)
4lg n, n2
n3
(3/2)n
2n
en
n 2n
22n
22n+1
n!
(n+1)!