Subsection 1.4.2 Argument (Proof)
A proof is an argument that applies one or more:
sound reasoning methods
to a collection of:
premises and definitions
to produce a conclusion that must be true whenever the facts are true.
The reasoning methods are general purpose. They’re the major focus of this course.
The premises and definitions must be chosen so that they model whatever situation(s) we want to reason about.

A formal proof typically looks something like this:
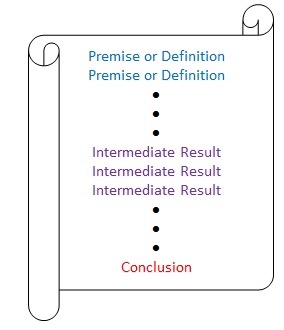
Each line of such a proof (other than the premise/definition lines) must follow logically from one or more of the preceding lines.
Activity 1.4.2.
Here’s an example of a simple proof. We reason first that, by virtue of being on the team, Alex is a student. Then, since all students must take final exams, Alex must do so.

In this class, we will spend some time practicing writing formal proofs in this way.
But often, both in everyday reasoning and in mathematics, we write arguments with a less rigid structure. That’s okay, as long as it’s clear what the premises/definitions are and it’s still true that every other claim we make is justified by the application of a sound logical rule to one or more claims that are known already to be true.
Activity 1.4.3.
Here’s a possibly more natural way to state the argument about Alex:
Alex must take final exams. Since he’s on the team he must be a student and all students have to take the exams.
Notice that, unlike in the formal structure, we actually wrote the conclusion first. That’s common. But don’t be fooled. The reasoning is the same. The conclusion follows from the premises.
Remark 1.4.1. Big Idea.
The tools of logic are premise-neutral. They can be stated in a general way and then applied to any premises we choose. Their job is to preserve truth. They will allow us to derive only claims that must be true whenever all the premises are true.
Problems 1.4.4.
Consider the following argument:
Jean is the President of the club. She’ll be at the party on Saturday. Everyone in the club is coming.
(a)
“Jean is the President of the club,” is a:
Premise.
Intermediate Result/Conclusion that could reasonably be derived from the other claims.
(b)
“Jean will be at the party on Saturday,” is a:
Premise
Intermediate Result/Conclusion that could reasonably be derived from the other claims.
(c)
“Everyone in the club is coming,” is a:
Premise
Intermediate Result/Conclusion that could reasonably be derived from the other claims.
(d)
Which of the following is a correct description of our argument:
It is correct (i. e., it uses only the given premises and reasons correctly to the conclusion.)
It isn’t quite right, but it would be if we made explicit one or more premises that are common knowledge.
It isn’t correct and it can’t easily be fixed by adding obvious premises.
