English Sentences versus Logical Statements

Subsection 1.2.4 English Sentences versus Logical Statements

The relationship between English declarative sentences and logical statements is not always straightforward. We’ll have a lot more to say about this in later chapters. But let’s just get a glimpse of the problem now so that we don’t get confused and worry that, because English is complicated, our logic must also be.

Subsubsection 1.2.4.1 Nonsense

Some English declarative sentences can’t be translated into logical statements because they don’t make sense (at least without assuming we’re in a cartoon or some other non-everyday world).

Activity 1.2.9.

A serving of pie has dragon calories.
The sister of our textbook is walking into class.
There are no people in 7.

All of these sentences are nonsense because of what we can call type conflicts. In each of them, we appear to be asserting a claim about some property of some object, but the object isn’t the kind of thing that can possess the stated property. 1 is nonsense because dragon isn’t a number. 2 is nonsense for a couple of reasons, but we’ll start with the fact that textbooks don’t have biological relatives. 3 is nonsense because 7 isn’t a set, so it doesn’t make sense to talk about whether or not something is in it.

Notice the difference between being nonsense and being false.

Activity 1.2.10.

Consider:

Pencils are fond of chocolate.

1 is nonsense. If it were simply false, then it's negation would have to be true (by the Law of the Excluded Middle). But that is:

Pencils are not fond of chocolate.

But this, too, is nonsense.

Compilers for programming languages are very clear about what it means for there to be a type conflict (as opposed to what it means for something to be false).

Activity 1.2.11.

In Python (just to pick one example):

\(7 + 1 > 0 \): executes and returns the value true
\(7 + 1 \lt 0 \): executes and returns the value false
\(abc + 1 > 0 \): produces the red message: \({\color {red} {Type Error} } \)

As we explore the use of our logical language, we’ll see that we can avoid writing nonsense by giving clear definitions for all of our terms and then using those terms in ways that are consistent with those definitions.

Problems 1.2.12.

For each of the following sentences, indicate whether or not there is a sensible interpretation that can be expressed as a logical statement. Don’t stretch to think of some metaphorical or imaginary interpretation that makes sense. Note that we are talking about making a sensible claim. Not necessarily a true one. Sensible claims can be false.

(a)

Spinach is fattening.

Sensible
Not sensible

Answer.

i is correct.

Solution.

Fattening is a property of foods. So this sentence makes sense, although it is false.

(b)

Pencils are optimistic.

Sensible
Not sensible

Answer.

ii is correct

Solution.

Optimism is a property of sentient beings and, in another sense, of situations. It doesn’t make sense to assert it of pencils

(c)

You can access the Internet on the moon.

Sensible
Not sensible

Answer.

i is correct.

Solution.

Accessibility of the Internet from a particular location is a well-defined property.

Subsubsection 1.2.4.2 Vagueness

Some English sentences don’t seem to have a truth value because they are vague or fuzzy.

Activity 1.2.13.

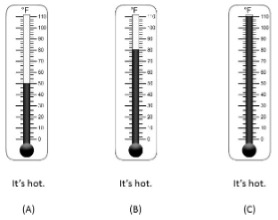
Consider the three situations shown here:

There is little disagreement that (A) is false.

There is little disagreement that (C) is true.

But what about (B)? The problem is that our notion of what it means to be “hot” is vague and it may depend on context.

If we want to translate English sentences like (A) – (C) into logical statements, we will first have to provide precise definitions of the predicates (like “hot”) that we are going to use.

Subsubsection 1.2.4.3 Presuppositions

Some seemingly simple English sentences can’t easily be translated into logical statements with truth values because they carry unstated assumptions.

Activity 1.2.14.

Consider:

[4] The king of France is bald.

Is this sentence true or false? It doesn’t feel false because there is no king of France with hair. But it doesn’t feel true because there is no bald King of France. We could translate this sentence into the following logical claim:

[4'] There is a king of France and that person is bald.

Now we can assign a truth value. This new sentence is clearly false.

Remark 1.2.6. English Aside:.

It’s not uncommon for English sentences to carry what are called presuppositions. A presupposition is a claim that the speaker/writer assumes is already shared with the audience. So, in the interest of efficient communication, it can simply be skipped. For example, “The king of France is bald,” carries the presupposition that there is a king of France. We tend to have difficulty assigning truth values to sentences (like [4]) that carry presuppositions that are false. Logicians and linguists have proposed various ways of solving this problem. One is the technique that we just used (which makes such sentences false). Another is just to say that such English sentences have no truth value.

The bottom line: While logical statements must be either true or false, that’s not necessarily so of English sentences. So we’ll have to be careful when we translate back and forth between the language of English and the language of logic.

Subsubsection 1.2.4.4 Practice

Problems 1.2.15.

We want to convert each of the following English sentences into a logical statement. But, in each case, there is a problem. Indicate, for each of the sentences, what that problem is.

(a)

The daily shuttle between New York and the moon leaves at 8:00 am.

The sentence doesn’t make sense because there’s a type conflict. (In other words, we are trying to assert that some object X has some property P but things like X can’t have property P.)
At least one of the terms used in the sentence is vague. Before we can translate the sentence into a logical statement, we’ll have to provide precise definitions of the vague terms.
The sentence carries a presupposition that is false. So if we want to convert it to a logical statement with a truth value, we’ll have add a clear statement of what that presupposition is.

Answer.

iii is correct

Solution.

This sentence carries the presupposition that there is a daily shuttle between New York and the moon. But that presupposition is false so it’s hard to assign a truth value to this claim taken alone. We could, instead, write, “There is a daily shuttle between New York and the moon and that shuttle leaves at 8:00 am.” Now we have an expression with a truth value: it is false.

(b)

The square root of Paris is Pygmalion.

The sentence doesn’t make sense because there’s a type conflict. (In other words, we are trying to assert that some object X has some property P but things like X can’t have property P.)
At least one of the terms used in the sentence is vague. Before we can translate the sentence into a logical statement, we’ll have to provide precise definitions of the vague terms.
The sentence carries a presupposition that is false. So if we want to convert it to a logical statement with a truth value, we’ll have add a clear statement of what that presupposition is.

Answer.

Solution.

Only numbers have square roots. Paris isn’t a number. Furthermore, if there were a square root, it too would have to be a number. Pygmalion isn’t a number.

(c)

Austin is a big city.

The sentence doesn’t make sense because there’s a type conflict. (In other words, we are trying to assert that some object X has some property P but things like X can’t have property P.)
At least one of the terms used in the sentence is vague. Before we can translate the sentence into a logical statement, we’ll have to provide precise definitions of the vague terms.
The sentence carries a presupposition that is false. So if we want to convert it to a logical statement with a truth value, we’ll have add a clear statement of what that presupposition is.

Answer.

ii is correct.

Solution.

If we want to be able to assign a truth value to this sentence, we’ll first have to provide a precise definition of what it means for a city to be big. Is a city of about a million people big? It will seem so to someone from a town of 5,000. But not to someone from a city of 20 million.