Subsection 8.12.2 Empirical Induction Leads the Way
Empirical induction often gives us a sensible basis for deciding how to act given the knowledge that we have at the moment.
But it does something else too: it can point us in a sensible direction. We can then look for a more robust way to prove claims that we think are very likely to be true.
Consider the Four Color Problem: Divide a plane (a flat surface) into contiguous regions. This can be done with straight lines or with curves. Call the resulting structure a map. Is it possible to color all of the regions of the map in such a way that no two regions that share a boundary (a single point doesn’t count) are colored in the same way?
In the mid-nineteenth century it was conjectured that the answer to this question was yes. A lot of people spent a lot of time looking at a lot maps, trying to find ones for which four colors were not enough. No luck.
Empirical induction thus suggested the truth of what is now known as the Four Color Theorem: Four colors suffice to color any planar map.
But many failures by many people do not a proof make. So the search was on. And, in 1976, a proof was found. By the way, that proof is significant for anyone interested in computation. It was a computer-assisted proof that checked 1,936 cases.
Empirical induction can be risky though and we must use it carefully. To see how hard it can be even to know what constitutes supporting evidence, consider this example:
Suppose that we want to argue the truth of the claim:
All people are less than 20 feet tallSuppose that we’ve looked at thousands of people and the tallest one has been under 9 feet tall. We may be ready to assert that we believe the claim. We haven’t found anyone even close to 20 feet tall. But suppose that we look just a little farther. And we find a 19 foot tall man. Officially, we’ve found another person who substantiates our claim. But, perhaps counterintuitively, most of us, on seeing this example, would think the claim less, rather than more likely to be true. Why? Because now, apparently, people can get at least close to the 20 foot mark.
Exercises Exercises
1.
How many colors are required to color this map (according to the rules of the Four Color Problem)?
1
2
3
4
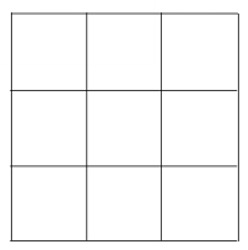
2.
How many colors are required to color this map (according to the rules of the Four Color Problem)?
1
2
3
4
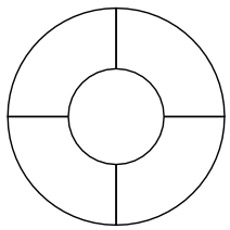
3.
How many colors are required to color this map (according to the rules of the Four Color Problem)?
1
2
3
4

Exercise Group.
Finding a proof or a counterexample for the Four Color Theorem was an open problem in mathematics for a long time. It isn’t any more.
But there are still other open problems. Here’s one. It has various names. We’ll call it the 3n+1 Problem.
Given any integer n, do the following until n = 1:
If n is even divide it by 2.
If n is odd, multiply it by 3 and add 1.
Now consider this question: Will the procedure given above always halt? In other words, regardless of the original value of n, must it eventually become 1?
Part 1.
Try it yourself. Suppose that n = 6. Counting both 6 and 1, how many values are computed before the procedure stops?
Correct answer: 9
Part 2.
(Part 2) Now try it with 16. How many values (including 16 and 1) are computed?
Nifty Aside
By the way, it is generally thought that this process does always halt by producing the value 1. The claim that is does so is called the Collatz Conjecture. No proof of it has yet been found. On the other hand, the search for a counterexample that would prove it false has also (so far) failed. If you want to try your hand at that search, go to:
http://www.nitrxgen.net/collatz.php


