Subsection 3.5.1 Introduction

If we wanted to make an apple pie, we might start with flour, sugar, apples, and such. This is called cooking “from scratch”. Alternatively, we could buy a pre-made pie shell and some apple filling and be 90% done. If we want to prove a Boolean logic theorem, we might build a truth table. On the other hand we might make faster progress using some pre-made theorems: the identities and inference rules of the previous sections.
Use of the identities and inference rules has three benefits over truth tables:
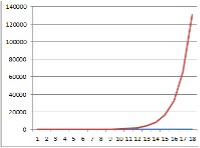
The size of a truth tables grows as where its corresponding statement has n operators and m variables. For even moderate m and n this can be huge.
Although a truth table, if completed correctly, produces a bullet-proof argument, there is almost no insight arising from the proof. We may know that something is true but we may have little understanding of why that is so.
The truth table approach does not generalize to more powerful logics, including predicate logic (which we’ll explore in the next section). There we’ll allow quantified predicates, so we’ll be able to say not just that Chris has a mother but also that all people have mothers. So, in particular, the truth table approach isn’t powerful enough to describe all of what, in everyday life, we call “correct reasoning”.
So we actually get a better “proof pie” if we “cheat” and skip the “from scratch” approach.
In much the same way as in the cooking example, we could consider writing computer code in a low level or a high level programing language. The high level language, which lets us build on code that has already been written, makes programming easier and leads to programs that are easier to understand.
We’re about to describe a proof technique that we call natural deduction . It will exploit the identities and inference rules that we’ve just been studying. We call this approach “natural deduction” to emphasize the fact that it corresponds to how humans think.
Exercises Exercises
1.
1. Consider the expression:
\(( ∧ ) ∨ (( ∧ ) ∨ ( ∧ )) → \)
How many rows are there in its truth table?
