Subsection 8.8.9 The Fibonacci Sequence
We’ve now seen that we can define a sequence of numbers by specifying one, or some small number, of starting values. Then we write a formula that computes the values of later elements from preceding ones.
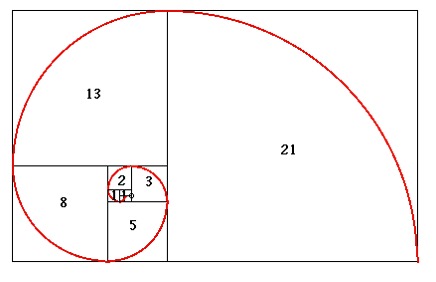
One of the best studied examples of such a sequence is this one:
Define the Fibonacci sequence as follows:
f1 = 1, (The first element is 1.)
f2 = 1, (So is the next one.)
for all k ≥ 2, fk+1 = fk + fk-1 (All other elements are computed from the two previous
The first several terms of the sequence are 1, 1, 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5=13.
Nifty Aside
The Fibonacci sequence has fascinated mathematicians for centuries. It is named for the Italian Leonardo Fibonacci (c 1170 – c 1250), who popularized it in Europe, although it was known before him in India. Fibonacci’s most important contribution to European mathematics was the number system we now use (often called Arabic numerals). Unlike the Roman system, it exploits an explicit representation for zero. But the sequence that bears his name is also important for many reasons, including its relationship to the golden ratio and its appearance in the natural structure of many plants.