Skip to main content

Subsection 8.5.1 The Key Idea – When One Value Depends on Another

So far, we’ve been able to prove (or disprove) claims by simply exhibiting a single example. But when an existential quantifier occurs inside the scope of another quantifier, it’s possible (in fact likely) that the required example depends on the value of the variable that is bound by the outside quantifier.

Consider:

x (y (MotherOf(y, x)))

Note that this claim is true although there is no single y who is the mother of everyone.

In such cases, what we need to do is to describe a procedure that, when given a value of one variable, finds an appropriate value for the dependent variable. We must of course also argue that our procedure is correct.

So a proof by construction generally has the structure:

  1. Describe the construction that produces the required value.

  2. Prove that the resulting value actually does have the necessary properties.

Video cover image

Sometimes we do the two parts in that order. Sometimes our argument for the correctness of the construction is part of our definition of the construction itself.

In the examples that follow, assume the standard axioms of arithmetic. Also assume that we can compute any standard arithmetic functions like addition and multiplication.

Consider the domain of integers. Prove: x (y (y > x2)).

The proof is by construction. Given any value x, the following procedure computes a value y that satisfies the claim:

y = x2 + 1

The value of y that is computed in this way must satisfy the claim: Since the domain is the integers, we have that x2  x. By adding 1, we guarantee that x2 > x.

Notice that we can think of proof by example and counterexample as special cases of proof by construction: We have a simple procedure that takes no input and simply returns the one required object.

Exercises Exercises

1.

Indicate, for each of the following graphs, whether or not it is regular:

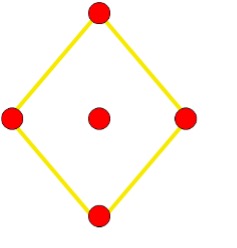
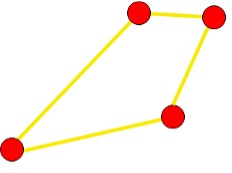
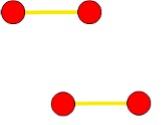
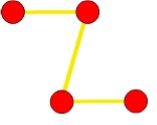
(a) (b) (c) (d)

Answer.

  1. not regular

  2. regular

  3. regular

  4. not regular

Solution.

  1. Explanation: In a regular graph, every node has the same degree. The four outside nodes have degree 2 (they each touch 2 edges). The inside node has degree 0.

  2. Explanation: Every node has degree 2.

  3. Explanation: All nodes have degree 1.

  4. Explanation: The first and last nodes in the chain have degree 1 The two in the middle have degree 2.

2.

Indicate, for each of the following graphs, whether or not it is cubic:

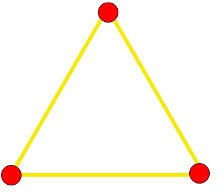
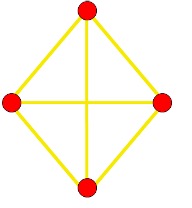
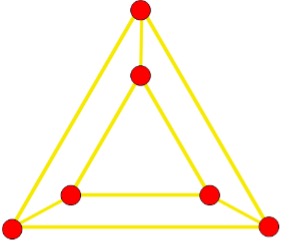
(a) (b) (c)

Answer.

  1. not cubic

  2. cubic

  3. cubic

Solution.

  1. Explanation: In a cubic graph, every node has degree 3. In this graph, every node has degree 2.

  2. Explanation: Every node has degree 3, so this graph is 3-regular or cubic.

  3. Explanation: Every node has degree 3.

3.

Prove by construction that, for every fixed length character string, there exists a longer one.

Consider the following candidates as constructions that prove our claim: Let s be the original string. Then these constructions return w, the required longer string. We use the symbol || for the concatenation operator. It simply glues the second string to the right end of the first one. So, for example, “hop” || “scotch” is “hopscotch”. Another example: “cake” || “”, is just “cake”. We call “” the empty string: it’s a string that happens not to contain any symbols.

  1. w = s || “a”

  2. w = s || s

  3. w = “a” || s

Which of these constructions is correct and proves our claim:

  1. Just I.

  2. Just II.

  3. Just III.

  4. Just two of them

  5. All three of them

Answer.
Corretct is correct D.
Solution.
Explanation: I and III are correct. Each creates a string that has one more character than does the original string s. You might be tempted to think that II is also correct. For example, if s = “bye”, then s || s = “byebye”, which is certainly longer than “bye”. But there is one case in which this doesn’t work. If s = “”, then s || s = “”.