Skip to main content

Subsection 8.7.1 The Key Idea

When we solve a problem, we often take actions that change something. That’s how we transform a “problem” into a “solution”. Perhaps counterintuitively, we can often prove useful properties about our actions or our solution by relying on one or more key things that don’t change as we solve the problem. We’ll call these things that don’t change invariants.

Consider a classic problem called the mutilated checkerboard.

Imagine that you are given a checkerboard that has been mutilated, as shown here. One square has been removed from each of two opposite corners.

Now consider the following question:

Can you cover the resulting mutilated board completely by placing nonoverlapping dominos on the squares? (Assume that each domino half exactly covers one checkerboard square.) Prove that your answer is correct.

What is your answer to this question? Hint: As you add dominos to the board, some things change. For example, the number of remaining empty squares decreases. You want to know whether it can decrease to 0. But is there some important property of the board that doesn’t change?

Exercises Exercises

Exercise Group.

Consider the following problem, which (following David Gries) we’ll call the coffee can problem: We have a coffee can that contains some white beans and some black beans. We perform the following operation on the beans:

Until no further beans can be removed do:

  1. Randomly choose two beans.

  2. If the two beans are the same color, then throw both of them away and add a new black bean.

  3. If the two beans are different colors, then throw away the black one and return the white one to the can.

It is easy to show that this process must halt. After each step, the number of beans in the can decreases by one. When only one bean remains, no further beans can be removed.

But what can we say about the one remaining bean? Is it white or black?

Part 1.

Suppose that the can starts with this collection of beans. What color is the remaining bean?

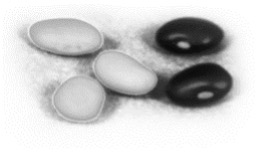
  1. White

  2. Black

Answer.
Correct answer is A.
Solution.
Part 2.

Suppose that the can starts with this collection of beans. What color is the remaining bean?

  1. White

  2. Black

Answer.
Correct answer is A.
Part 3.

Suppose that the can starts with this collection of beans. What color is the remaining bean.

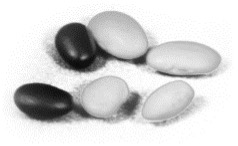
  1. White

  2. Black

Answer.
Correct answer is B.
Part 4.

Suppose that the can starts with this collection of beans. What color is the remaining bean?

  1. White

  2. Black

Answer.
Correct answer is A.
Part 5.

Suppose that the can starts with this collection of beans. What color is the remaining bean?

  1. White

  2. Black

Answer.
Correct answer is B.

Exercise Group.

Now we’d like to generalize and make a statement about what color the last bean will be. To help us do that, a useful step will be to write down an explicit description of what can happen at each iteration. The rules are given above. Answer these questions to describe them:

If two white beans are chosen, then:

  • How does the number of black beans change?

  • How does the number of white beans change?

If two black beans are chosen, then:

  • How does the number of black beans change?

  • How does the number of white beans change?

If one black bean and one white bean are chosen, then:

  • How does the number of black beans change?

  • How does the number of white beans change?

Part 1.

Now can you describe a pattern that lets you tell, for an arbitrary starting collection of beans, what color the last bean will be? Hint: Is there an invariant that helps? Look back at what happens in each of the three cases described above. Is there some important property that doesn’t change?

  1. It is possible to predict the outcome knowing just the initial number of white beans.

  2. It is possible to predict the outcome knowing just the initial number of black beans.

  3. It is possible to predict the outcome but it’s necessary to know something about the initial numbers of both white beans and black beans.

  4. It is possible to predict the outcome without knowing anything about the initial numbers of white or black beans.

  5. It isn’t possible in any simple way to predict the outcome.

Answer.

Correct answer is A.

Part 2.

Which one of the following is true:

  1. There is a useful invariant property of the number of white beans.

  2. There is a useful invariant property of the number of black beans.

  3. There is a useful invariant property that involves both the number of white and black beans.

  4. There is no useful invariant property.

Answer.
Correct answer is A
Solution.
Explanation: If the original number of white beans is odd, the remaining bean is white. Otherwise the remaining bean is black. To see why this is true, we note that our bean culling process preserves white bean parity (i.e., the state of being either even or odd). In other words, if the number of white beans starts out even, it stays even. If the number of white beans starts out odd, it stays odd. To prove that this is so, look again at the three rules. In each of them, an even number (either 0 or 2) of white beans is removed and white bean parity is preserved. So, if the number of white beans is initially odd, the number of white beans can never become zero and a white bean must be the sole survivor. If, on the other hand, the number of white beans is initially even, it can never become odd. So, in particular, it cannot become one. Thus any sole survivor must be black.

Exercise Group.

Now consider the Daisy Petal Game. There are two players. When the game starts, there’s a daisy with 18 petals. The players alternate turns. At his turn, a player may remove a single petal or a pair of adjacent petals (where adjacent means that the petals were adjacent in the original flower, before any petals were removed). The player who removes the last petal wins.

We want to answer the question, “Is there a guaranteed winning strategy?” And we want to prove that that answer is correct.

If you’d like to play the game to help you understand it, you can. Visit

http://www.novelgames.com/en/spgames/daisy/ 1 

Let’s start our analysis by considering a couple of simpler versions of the problem. Suppose that there are initially only 4 petals.

Should you elect to play first or second?

Now imagine that the petals are numbered 1 – 4 and consider:

  1. If your opponent moves first and takes petal 1, what should you do?

  2. If your opponent moves first and takes petals 1 and 2, what should you do?

Now suppose that there are initially 6 petals, numbered 1 – 6:

  1. If your opponent moves first and takes petal 1, what should you do?

  2. If your opponent moves first and takes petals 1 and 2, what should you do?

Now try it with a flower with 8 original petals. Can you see a pattern?

Part 1.

Which of the following is true? (Before you answer this, you should have in mind a winning strategy, if there is one, or an argument for why no such strategy exists.)

  1. There is a guaranteed winning strategy for the player who plays first.

  2. There is a guaranteed winning strategy for the player who plays second.

  3. There is no guaranteed winning strategy for either player.

Answer.
Correct answer is B.
Part 2.

Which of the following is true:

  1. There is a useful invariant property of just the number of remaining petals, regardless of which ones there are.

  2. There is a useful invariant property of the number of remaining petals but it also matters which ones they are.

  3. There is no useful invariant property.

See the Appendix for a discussion of our solution to this problem.

Answer.
Correct answer is B.
Solution.

Explanation: There is a winning strategy for the player who plays second. The idea is to preserve the following invariant:

There is a move that can be made (i.e. it’s not true that all petals have already been removed). You lose only if there is no move that you can make, so if this claim is always true when it’s your turn, you cannot lose.

Specifically, one such move is to mirror the opponent’s last move by removing the same number of petals and, more specifically, those that are exactly opposite the ones the opponent just took. (By opposite we mean the petals that you get by following a straight line from the opponent’s petals through the middle of the flower.) The following pictures illustrate the idea. If your opponent moves as in (A), you should move as in (B). If your opponent takes two petals, as in (C), you should also take two, as in (D).

What about the claim that the invariant always holds for the second player (in, other words, player 2 hasn’t lost yet)? Must it be true? It is true right after the first time that player 1 moves since the number of initial petals is even (and thus there are opposite petals). And it can be maintained by player 2 throughout the game. Since after each of player 1’s moves, player 2 takes the opposite petal(s), player 1 is forced next to take other petal(s) whose opposite(s) are still available to player 2.

Novel Games