CS 384G Final Project Water rendering raytracer
By David Nguyen
Objective For my final project, a particle based water model was developed loosely based on the Navier-Stokes equations. The particle system is rendered in a ray tracer to allow for refraction through the particles. This should allow for realistic looking water rendering . In order to do so, a heavy portion of the project utilized code from the raytracer and the animator from project 2 and 3 respectively.
Theory The Navier-Stokes equations are the quasi-essential equations of aerospace engineering which dictate how a fluid will behave. Any computational fluid dynamics software will attempt to solve those equations.
The equation above can be applied in the other orthogonal directions as well and represent the full 3D representation of the flow. While these equations represent the flow in an Eulerian point of view, a particle based model really represents a Lagragian point of view of the fluid, that is the properties of the fluid follow the particles. In other words, a particle system does not employ a grid and attempt to solve the Navier Stokes equations in a specific domain. However, my fluid model borrows certain terms from the Navier-Stokes equations, mainly the gravitational forces and the dp/dy term which represent the change in pressure over a distance y. These two forces create a momentum change in the particle which causes them to move toward some direction. The shear diffusion and fluid convection terms are not utilized due to their complexity and lack of time. Implementation Due to the shear amount of different flow (cascade, pipe, steady, unsteady, etc…) available to simulate, I chose to only model a jet flow, such as a fountain. The water particles feel a pressure gradient which causes them to rise, and gravity forces which causes them to fall. As they fall, they collide with objects in the scene. They lose their kinetic energy due to friction and surface tension. I implemented this by showing them slowing down parallel to the wall they struck and eventually disappearing. I also modified the user interface so that the user can input the location, initial velocity, initial pressure, number of particles, radius and spread of the particles. Position, velocity and pressure are self-explanatory. The radius of the sphere is how big the water particles look, and the spread is basically how big the particle jet is, or in other words, how far apart particles are when they form a j
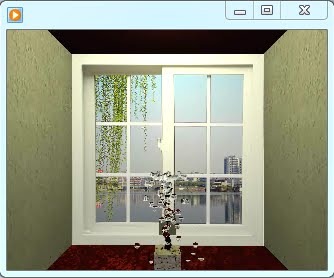
To run the particle system, I implemented an Euler explicit time scheme, due to its simplicity and quickness. The time step was chosen so that the particles do not behave erratically and cause the solution to explode. The Euler method uses the sum of forces to calculate the acceleration, which then is used to update the velocity at the next time step. The position is updated based on the new velocity. The Euler scheme is implemented in the Particle::update method(), which is then called by the raytracer::updateWater() function. Collision between water particles was not implemented due to high complexity and the fact that water does not behave in an elastic manner. However, collision between geometries and particle was implemented, with an algorithm similar to the one used for ray tracers. When a particle checks for potential collision, an isect object and a ray are created from the center of the particle, with the ray position being the center of the particle and the ray direction being the velocity vector. That ray is transformed from global to local coordinate system, where each type of geometries (box, square, sphere, etc…) checks for water collision. The algorithm for which they check collision is similar to one with a ray of light; the main difference here is that t, which is the parameter of distance between ray position and geometry intersection, must be smaller than the velocity of the particle multiplied by the timestep used during the Euler scheme iteration. Artifact Below is a raytraced movie of water in a “fountain” inside a room. The background is chosen so that the refraction can be better appreciated. References Panton, Ronald. “Incompressible Flow” 3rd edition John Wileys & Sons. 2005. |
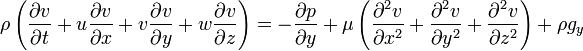
_text_