Fast Similarity Search for Learned Metrics

Brian Kulis, Prateek Jain, Kristen Grauman


Summary

We introduce a method that enables scalable similarity search for learned metrics. Given pairwise similarity and dissimilarity constraints between some examples, we learn a Mahalanobis distance function that captures the examples’ underlying relationships well. To allow sub-linear time similarity search under the learned metric, we show how to encode the learned metric parameterization into randomized locality-sensitive hash functions. We further formulate an indirect solution that enables metric learning and hashing for vector spaces whose high dimensionality make it infeasible to learn an explicit transformation over the feature dimensions. We demonstrate the approach applied to a variety of image datasets, as well as a systems dataset. The learned metrics improve accuracy relative to commonly-used metric baselines, while our hashing construction enables efficient indexing with learned distances and very large databases.


Overview of our approach
Motivation for searching with learned metrics.  A good distance metric between images accurately reflects the true underlying relationships, e.g., the category labels or other hidden parameters. It should report small distances for examples that are similar in the parameter space of interest (or that share a class label), and large distances for unrelated examples. Recent advances in metric learning make it possible to learn distance functions that are more effective for a given problem, provided some partially labeled data or constraints are available.  Many existing metric learning algorithms learn the parameters of a Mahalanobis distance.  By taking advantage of the prior information, these techniques offer improved accuracy when indexing examples.


Problem.  How can we search efficiently with such a specialized learned metric?  We want to be able to use these metrics to query a very large image database—potentially on the order of millions of examples or more. Certainly, a naive linear scan that compares the query against every database image is not feasible, even if the metric itself is efficient. Unfortunately, traditional methods for fast search (e.g, k-d trees, metric trees), cannot guarantee low query time performance for arbitrary specialized metrics.


Locality-Sensitive Hashing.  We construct a new family of hash functions that will satisfy the locality-sensitivity requirement that is central to existing randomized algorithms [Indky & Motwani, STOC 1998, Charikar STOC 2002] for approximate nearest neighbor search.  LSH guarantees sub-linear time retrieval with a bounded approximation error; the main idea is to derive a hash function such that the more similar two items are, the more likely they are to collide in the hash table.  To use LSH for search, one must be able to provide a family of hash functions that are locality-sensitive for the similarity function of interest.  See Figure 1.



LSH
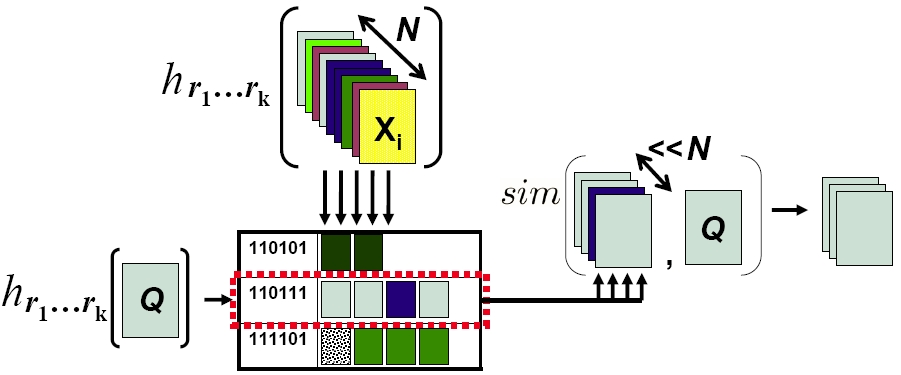Figure 1: Overview of locality-sensitive hashing (LSH [Indyk & Motwani 1999, Charikar 2002]).  A list of k hash functions are applied to map N database examples into a hash table where similar items are likely to share a bucket.  After hashing a query Q, one must only evaluate the similarity between Q and the database examples with which it collides to obtain the approximate nearest-neighbors. 




Our idea: Semi-Supervised Locality-Sensitive Hash Functions.  While existing hash functions could handle similarity measures such as Hamming distance, inner products, or L_p norms, our main contribution is to derive hash functions that will respect the learned Mahanobis distance or kernel function.  We accomplish this by deriving hash functions that are "biased" according to the similarity constraints that train the metric: we want less similar examples to fall in different hash buckets (even if the raw similarity between them originally maps them to be close together), whereas we want more similar examples to be more likely to fall into the same hash bucket (even if the raw similarity suggested they were further apart).  See Figure 2.


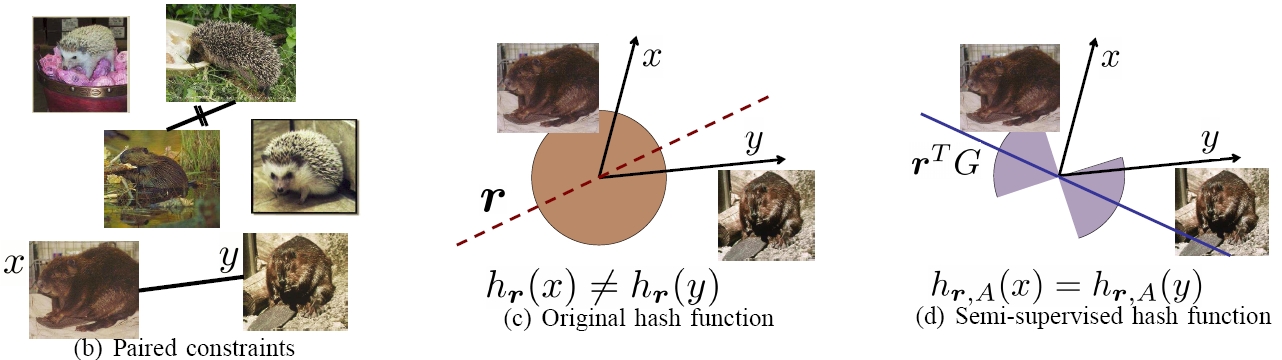Semi-supervised hash functions
Figure 2:  (b) When learning a metric, some paired constraints can be obtained for a portion of the image database, specifying some examples that ought to be treated as similar (straight line) or dissimilar (crossed out line). (c) Whereas existing randomized LSH functions hash examples similar under the original distance together, (d) our semi-supervised hash functions incorporate the learned constraints, so that examples constrained to be similar—or other pairs like them—will with high probability hash together. The circular red region in (c) denotes that the existing LSH functions generate a hyperplane uniformly at random to separate images, in contrast, as indicated by the blue “hourglass” region in (d), our hash functions bias the selection of random hyperplane to reflect the specified (dis)similarity constraints. In this example, even though the measured angle between x and y is wide, our semi-supervised hash functions are unlikely to split them into different buckets since the constraints indicate they should be treated as similar.




For very high-dimensional data, explicit input space computations are infeasible.  We show how to compute the desired hash function in terms of a series of weighted comparisons to the points participating in similarity constraints---without needing to explicitly access the learned Mahalanobis parameters. 

Our method is applicable to general learned Mahalanobis metrics (e.g., where the initial "base metric" is Euclidean distance), and we also show how to embed two useful image matching kernels (PMK and PDK) so that they can be used with semi-supervised hash functions.  See [Kulis et al. PAMI 2009 and Jain et al. CVPR 2008] for details. 

While we are especially interested in the visual search problem, our algorithm is not specific to image features, and is also applicable to descriptors for other domains (e.g., text, bio, etc.).


Example results
The figures below show some example results.  Please see our papers for more examples.
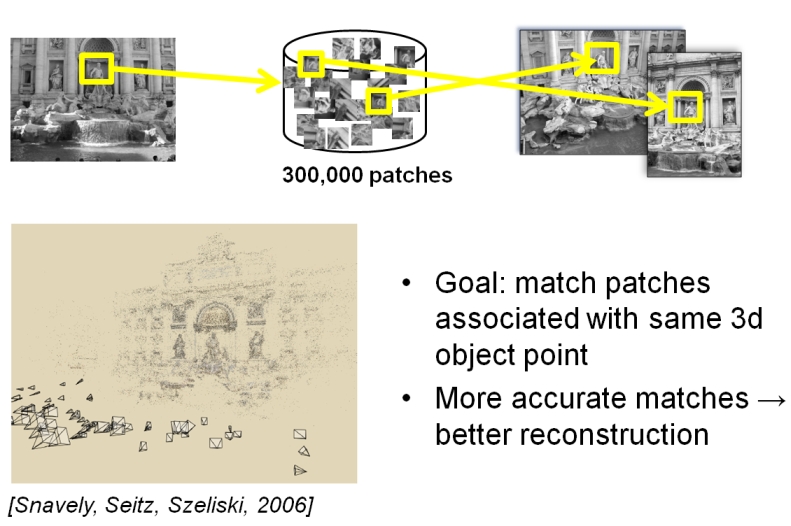
photo tourism data
 Result1
Figure 3: Result on the PhotoTourism patch dataset.  We generate similarity constraints based on true correspondences in the training data.  Given a new image, we want to search for similar patches.  The plot shows that the learned metric provides better retrieval of similar patches, and that our semi-supervised hash functions make it possible to search only a fraction of the entire pool to find the best matches.

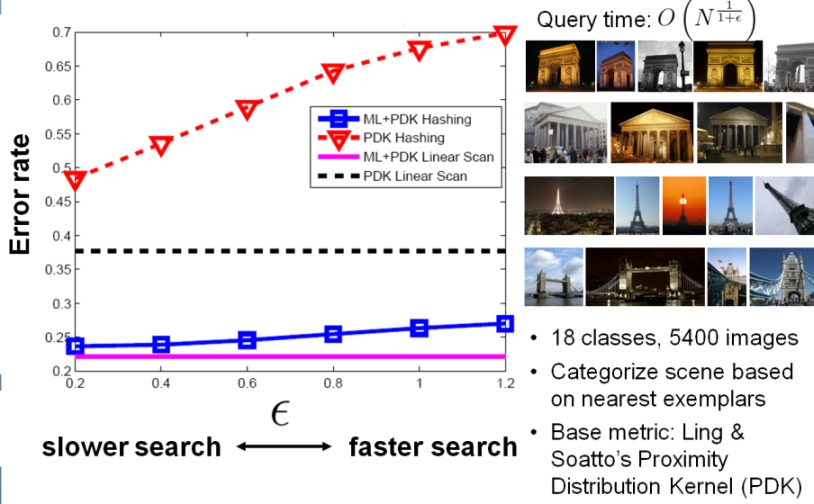Flickr scenes result
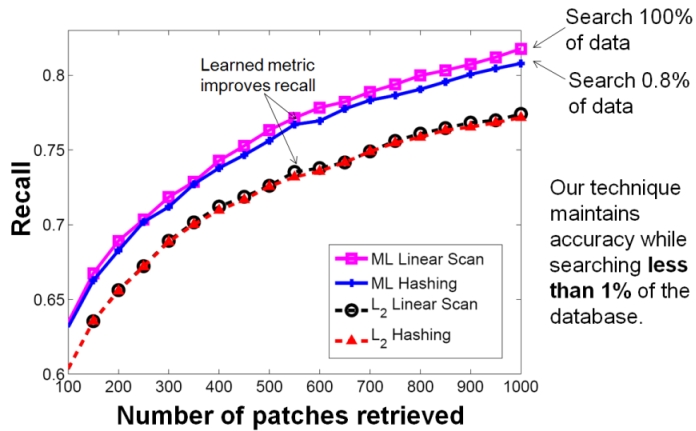
Figure 4: Result on the Flickr Scenes dataset.  The goal is to take a query image and retrieve images of the same tourist location.  We generate similarity constraints based on some labeled examples (same-class pairs form similarity constraints, different-class pairs form dissimilarity constraints).  The learned proximity distribution kernel gives lower error (compare pink curve to dotted black curve), and our semi-supervised hash functions make it possible to search with that more accurate measure much more efficiently (blue curve).  For epsilon = 1.2, we are searching only 3% of all the database images, and achieving an error rate very close to linear scan's.


Online extension

In [Jain et al. NIPS 2008] we show how to dynamically update the hash tables as the learned metric is updated in an online manner.  The above description assumes that the set of similarity constraints have been given to us all at once.  However, in many real applications it may happen that new constraints (supervision) are obtained gradually, and we want to be able to field queries at any intermediate point in time.  Rather than re-hash all database examples from scratch once (which would take linear time in the number of stored points), we introduce an algorithm to incrementally update the hash keys for the stored data.  Essentially, we predict which bits in the keys are most likely to flip given the adjustments to the constraints and learned distance function.  See Figure 4.
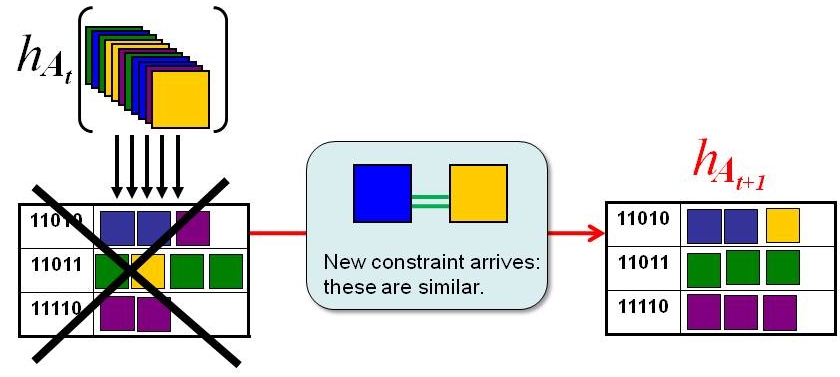Online hash table updates
Figure 4:  If the hash table is constructed to preserve the similarity according to a certain learned metric (A_t), then once new similarity constraints require updates to the metric (A_{t+1}), the original hash table becomes obsolete.  For example, in this schematic, the points are originally arranged into the buckets on the left.  Then some new constraint comes in that says "blue" and "yellow" points should be treated as similar.  Note that in the old hash table, blues and yellows did not share a bucket.  Rather than simply rehash, we show how to dynamically update the hash keys so that the revised metric is correctly preserved (with high probability).




References
Fast Similarity Search for Learned Metrics.   B. Kulis, P. Jain, and K. Grauman.   In IEEE Transactions on Pattern Analysis and Machine Intelligence (TPAMI), Vol. 31, No. 12, December, 2009.  [link]

Fast Image Search for Learned Metrics.  P. Jain, B. Kulis, and K. Grauman.  In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, Alaska, June 2008. [pdf]

Online Metric Learning and Fast Similarity Search.  P. Jain, B. Kulis, I. Dhillon, and K. Grauman.  In Advances in Neural Information Processing Systems (NIPS), Vancouver, Canada, December 2008.  [pdf]


Acknowledgements: This work is supported in part by NSF CAREER IIS-0747356.