C S 384G Final Project: Path Tracer

PATH TRACING

Path tracing [Kajiya 1986] is a derivative of Whitted-style [1980] ray tracing, where the view rays do not branch into recursive shadow, reflection, and transmission subsequent rays. Instead, at each ray-object intersection, the next ray is chosen stochastically according to the scattering function of the surface intersected. To compensate for the lack of branching, an increased number of view rays are traced into the scene. This increased sampling at the view ray level is often needed for other reasons, such as antialiasing. Path tracing allows super-sampling to be consolidated at the view level.

Since Whitted-style ray tracing originates multiple rays at each ray-object intersection, computation is spent on deeper parts of the tree of rays. An important property of path tracing vice Whitted-style ray tracing is the computational emphasis on the low-depth (fewer bounce) rays. Since, generally, low-depth rays contribute more to the resulting image than high-depth rays, path tracing’s computation time is proportionate to the resulting contribution.

This proportionality concept is also applied to the scattering of rays at ray-object intersections. Conceptually, the scattering function could be uniformly sampled over its entire sphere, but that would be computationally wasteful — many rays would be traced that contribute little or nothing to the resulting image. Instead, the scattering function is sampled preferentially in directions that are likely to contribute more to the resulting image. This is known as importance sampling.

The Rendering Equation

Kajiya’s 1986 paper focuses on a more rigorous analytical treatment of rendering than had been in use at the time. He uses concepts from thermodynamics to formulate what he named the rendering equation:

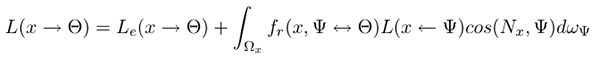
This equation states simply that the “intensity” of light travelling from one point p to another q is determined by:

• Geometric obstructions between p and q
• Emission of light from p to q
• The sum, for all surfaces in the scene, of the intensity of light cast on q multiplied the reflectance of this light from q to p.

This formulation as an integral, based on physical principles, converts the problem of rendering a scene into the problem of evaluating the rendering equation. This gives us the ability to apply new analytical tools to rendering.

Monte Carlo Integration

The path tracing approach described above is such a tool. Evaluating the integral stochastically in the manner of path tracing is an application of Monte Carlo techniques to the rendering equation. Kajiya details the derivation of this in his paper. Cook [1984] uses stochastic scattering of rays to produce effects of gloss, translucency, penumbras, depth of field, and motion blur, although the paper did not present it as a Monte Carlo integration.

Bidirectional Scattering Distribution Function

Path tracing traces rays to intersections with surfaces of materials in the scene. It then evaluates a portion of the rendering equation at that ray-object intersection. The reflectance factor in this case is a function of the material at the intersection and the inbound and outbound ray angles to the surface normal. Conventionally, the reflectance is specified as two factors: the cosine factor to account for the projection of the inbound (light-side) ray on the surface, and the bidirectional reflectance distribution function (BRDF) [Nicodemus 1977]. In the case of our path tracer, we consider scattering in both the reflected and refracted (transmitted) directions. Transmission has an equivalent to the BRDF, the bidirectional transmittance distribution function (BTDF). Combined, they are known as the bidirectional scattering distribution function (BSDF).

Importance Sampling

Given a BSDF, conceptually, the information for importance sampling can be derived and used. Since the goal of importance sampling is to trace rays in the direction will contribute the most to the resultant image. This is begging the question: we need to know the solution to tracing the ray to determine if we want to trace it.

So, instead, we determine the “more likely to contribute” scattering directions by evaluating the BSDF in its general form and using that as a probability density function to choose scattering directions.

This is easier said than done, of course. In fact, Kajiya didn’t implement it for the path tracer in his 1986 paper. There are some simple cases, however:

• Perfectly absorbent surface: Don’t scatter, absorb ray.
• Perfectly mirror reflective surface: There is exactly one direction that will contribute, so scatter in that direction. (The BRDF is a Dirac delta.)
• Perfectly lens-transmissive surface: Similarly, there is exactly one direction that will contribute, so scatter in that direction.

For other BSDFs, there are a few with published importance samples, for example Phong [Lawrence et al. 2002], Blinn, and LaFortune. Lawrence et al. [2004] discuss approaches for importance sampling of BRDFs without a known analytical solution.

THIS PATH TRACER IMPLEMENTATION

The software developed as part of this project derives from a conventional ray tracer, and makes the following changes:

I refactored the RayTracer class into an abstract RayTracer class that owns the scene graph and image buffer, and concrete subclasses RecursiveRayTracer and PathTracer that implement a tracePixel method using their particular algorithm.

The RecursiveRayTracer is identical to the “ray” project (project 3).

The PathTracer class uses pixel level supersampling (using a uniform random distribution) to trace multiple view rays per pixel.

When traced rays intersect with an object, direct lighting is evaluated conventionally, using a Phong shader and shadow rays to the lights in the scene. If the ray has not reached a deterministic maximum depth, indirect lighting is evaluated by recursively tracing a ray scattered in a single direction according to the importance sampling function and BSDF.

The use of shadow rays for direct lighting in addition to the scattered rays for indirect lighting, strictly speaking, means traced rays do not form pure “paths”. But shadow rays are not recursive, and the direct lighting nearly always contributes dramatically to the traced ray’s luminance, so this is an important optimization. Is is consistent with Kajiya’s description of the path tracing algorithm.

The PathTracer class, in turn, uses concrete subclasses of an abstract BSDF class to determine rays scattering angles and to determine reflectance. Currently, we have implemented two BSDFs: a perfect mirror/lens reflectance/transmission and a Phong reflectance with perfect transmission.

Other Implementation Items

Added UI elements so user can pick BSDF at runtime.

Created a Cornell Box SBT-raytracer (.ray) data file from Cornell's raw measurements.

Fixed a few bugs in the “ray” framework:

• Fixed ray::operator= failure to copy ray type
• Now checks for UI events reasonably frequently
• Fixed deadlock on pressing the Stop button (or closing window) during tracing
• General software engineering cleanup of the “ray” framework; Eliminated about 1000 compiler warnings; “-Wall” still lists about 2000 warnings, though :-(

Added a few "niceties" to the “ray” framework:

• Object names in intersection debug output (needed to fix parser for this)
• Correct menu layout and keyboard shortcuts on Mac OS
• Better UI defaults for path tracing
• Uses FLTK image read Fl_Shared_Image class, instead of the functions in bitmap.cpp: Consequece: not broken on big-endian CPUs, and can read PNG, JPEG, PNM, PBM, PGM, PPM, or BMP image fomats for texture maps, etc.

APPENDIX: ADDITIONAL MATERIAL

• Presentation slides (updated): Stochastic Ray Tracing (PDF format, 552 kB)
• Software: Available upon request
• Artifacts:
  • Path traced Cornell box image 625 paths/pixel, max depth 10 (PNG format, 287 kB)
  • Path traced scene with Phong BSDF 625 paths/pixel, max depth 10 (PNG format, 79 kB) — contrast with Original ray-traced scene (project 2) (PNG format, 76 kB)

ACKNOWLEDGMENTS

The code base used for the path tracer was derived from the “ray” package supplied by Prof. D. Fussell, Dept. of Computer Science, The University of Texas at Austin, which was adapted from CSE 557, Copyright © 1993-2008, Department of Computer Science and Engineering, University of Washington.

BIBLIOGRAPHY

Ashikhmin, M. and Shirley, P. 2000. An anisotropic phong BRDF model. J. Graph. Tools 5, 2 (Feb. 2000), 25-32.

Bekaert, P., Sbert, M., and Halton, J. 2002. Accelerating path tracing by re-using paths. In Proceedings of the 13th Eurographics Workshop on Rendering (Pisa, Italy, June 26- 28, 2002). S. Gibson and P. Debevec, Eds. ACM International Conference Proceeding Series, vol. 28. Eurographics Association, Aire-la-Ville, Switzerland, 125-134.

Cline, D., Talbot, J., and Egbert, P. 2005. Energy redistribution path tracing. In ACM SIGGRAPH 2005 Papers (Los Angeles, California, July 31 - August 04, 2005). J. Marks, Ed. SIGGRAPH '05. ACM, New York, NY, 1186-1195.

Cook, R. L. 1986. Stochastic sampling in computer graphics. ACM Trans. Graph. 5, 1 (Jan. 1986), 51-72..

Cook, R. L., Porter, T., and Carpenter, L. 1984. Distributed ray tracing. In Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques. H. Christiansen, Ed. SIGGRAPH '84. ACM, New York, NY, 137-145.

Dutré, P., Jensen, H. W., Arvo, J., Bala, K., Bekaert, P., Marschner, S., and Pharr, M. 2004. State of the art in Monte Carlo global illumination. In ACM SIGGRAPH 2004 Course Notes (Los Angeles, CA, August 08 - 12, 2004). SIGGRAPH '04. ACM, New York, NY, 5.

Goral, C. M., Torrance, K. E., Greenberg, D. P., and Battaile, B. 1984. Modeling the interaction of light between diffuse surfaces. In Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques. H. Christiansen, Ed. SIGGRAPH '84. ACM, New York, NY, 213-222.

He, X. D., Torrance, K. E., Sillion, F. X., and Greenberg, D. P. 1991. A comprehensive physical model for light reflection. In Proceedings of the 18th Annual Conference on Computer Graphics and Interactive Techniques. SIGGRAPH '91. ACM, New York, NY, 175-186.

Jensen, H. W., Arvo, J., Fajaro, M., Hanrahan, P., Mitchell, D., Pharr, M., and Shirley, P. 2001. State of the art in Monte Carlo ray tracing for realistic image synthesis. In ACM SIGGRAPH 2001 Course Notes. SIGGRAPH 2004. ACM, New York, NY.

Jensen, H. W. and Christensen, P. 2007. High quality rendering using ray tracing and photon mapping. In ACM SIGGRAPH 2007 Courses (San Diego, California, August 05 - 09, 2007). SIGGRAPH '07. ACM, New York, NY, 1.

Kajiya, J. T. 1985. Anisotropic reflection models. In Proceedings of the 12th Annual Conference on Computer Graphics and Interactive Techniques. SIGGRAPH '85. ACM, New York, NY, 15-21.

Kajiya, J. T. 1986. The rendering equation. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques. D. C. Evans and R. J. Athay, Eds. SIGGRAPH '86. ACM, New York, NY, 143-150.

Lafortune, E. P. and Willems, Y. D. 1994 Using the Modified Phong brdf for Physically Based Rendering, Report CW197, Department of Computer Science, K.U. Leuven, Belgium.

Lafortune, E. P., Foo, S., Torrance, K. E., and Greenberg, D. P. 1997. Non-linear approximation of reflectance functions. In Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques. SIGGRAPH '97. ACM Press/Addison-Wesley Publishing Co., New York, NY, 117-126.

Lawrence, J. 2002. Importance Sampling of the Phong Reflectance Model. Located at: https://www.cs.virginia.edu/~jdl/importance.doc

Lawrence, J., Rusinkiewicz, S., and Ramamoorthi, R. 2004. Efficient BRDF importance sampling using a factored representation. In ACM SIGGRAPH 2004 Papers (Los Angeles, California, August 08 - 12, 2004). J. Marks, Ed. SIGGRAPH '04. ACM, New York, NY, 496-505.

Lee, M. E., Redner, R. A., and Uselton, S. P. 1985. Statistically optimized sampling for distributed ray tracing. In Proceedings of the 12th Annual Conference on Computer Graphics and Interactive Techniques. SIGGRAPH '85. ACM, New York, NY, 61-68.

Nicodemus, F. E., Richmond, J. C., Hsia, J. J., Ginsberg, I. W., and Limperis, T. 1977. Geometric Considerations and Nomenclature for Reflectance. Monograph 160. National Bureau of Standards: Washington, DC.

Shirley, P., Smits, B., Hu, H., and Lafortune, E. 1997. A practitioners' assessment of light reflection models. In Proceedings of the 5th Pacific Conference on Computer Graphics and Applications (October 13 - 16, 1997). PG. IEEE Computer Society, Washington, DC, 40.

Shirley, P., Wang, C., and Zimmerman, K. 1996. Monte Carlo techniques for direct lighting calculations. ACM Trans. Graph. 15, 1 (Jan. 1996), 1-36.

Whitted, T. 1980. An improved illumination model for shaded display. Commun. ACM 23, 6 (Jun. 1980), 343-349.