 |
Optimizing Kick
Please note that the information presented here reflects the status of this project when it was presented to Peter Stone's Autonomous Robots course. See the associated publication for the current version of the work.
Goals
- Optimize the power of an Aibo kick using a machine learning approach.
- Create a parameterized Aibo kick capable of kicking the ball a requested distance.
Abstract
Coordinating complex motion sequences has always been a challenging task for robotics. This work demonstrates that machine learning can effectively and efficiently learn high dimensional kicking motion sequences on physical robots. The power of the resulting learned kick is on par with the most powerful hand-coded kicks but uses a very different kicking style. Finally, model inversion is applied to the problem of creating a parameterized kick capable of kicking the ball a requested distance.
Motivation
The Aibo ERS-7 is a commercial robot developed by Sony which was used for several years to compete in the Robocup Soccer League. As such, a primary challenge for Robocup teams was to program teams of ERS7 to score goals quickly and efficiently. A large factor in the success of an attack is the ability to provide the Aibo with a quick, powerful, and accurate kick.
 |
The Passing Challenge[12], a Robocup sub-competition, highlights the necessity of powerful and accurate kicks. The goal of the challenge is for three robots to pass the ball to each other in a circular pattern with the constraint that each Aibo must remain inside of its black circle. Because the Aibos are not allowed to leave the 35-cm circles, a single inaccurate kick will end the round of passing. Thus, a reliably accurate kick capable of traversing the maximum circle separation of 200cm is a necessity for this challenge. This work seeks to use machine learning techniques to learn a powerful kick capable of traversing a 200cm distance with as much accuracy as possible.
While powerful kicks can certainly reach the receiving Aibo, we hypothesize that like real soccer, it's harder to receive very fast kicks than those with more reasonable velocity. We seek to address this problem by learning a parameterized kick capable of accurately propelling the ball a requested distance. Using this parameterized kick, the passing Aibo can first judge the distance to the receiving Aibo and modulate the power of the kick accordingly.
Related Work
Past work has learned to optimize different skills on the Aibo:
Kohl and Stone[7][8] employed a variety of learning algorithms in order to optimize Aibo walk speed. They compare hill climbing, amoeba, genetic algorithms, and policy gradient algorithms to empirically establish how fast each is to optimize a parameterized walk. The task is constructed in such a way that the only human interaction necessary is changing the Aibo's batteries when depleted. Results show the learned walked significantly outperforms the best hand-coded walks and rivals other learned walks of the time.
Similarly, Saggar et. al[10] employed Kohl's framework in order to optimize a walk for both speed and stability. By incorporating a camera stability metric into the objective function, Saggar is able to demonstrate the trade-off between walk speed and visual accuracy. The final learned walk is demonstrated to sacrifice only a small amount of speed in exchange for superior camera stability.
The ball-grasping skill was optimized by Fidelman and Stone[4][5] using a layered learning[11] framework. The ball grasp consists of the Aibo pinching the ball beneath its chin and is an essential yet tricky step in controlling the ball before kicking. The layered learning architecture used in this work consisted of two layers, a lower level gait optimization layer, employing Kohl's walk optimization methods, and a higher level, novel, ball-grasping layer. Fidelman demonstrates that the layered learning approach can save time in comparison to a manual tuning approach. The success rate of the final ball grasping behavior shows significant improvements over hand-coded ball grasping procedures. Like previous walk optimization papers, Fidelman creates an autonomous learning environment in which the Aibo can repetitively approach, grasp, and relocate the ball without requiring human assistance.
Kobayashi et al[6] learn how to trap the ball using a reinforcement learning framework. Trapping, as opposed to grasping, is the process of intercepting and capturing a moving ball rather than a stationary one. Typically, this skill is useful when receiving passes. In order to automate the learning process, a ramp with rails is placed in front of the robot, allowing the robot to repeatedly kick and trap the ball. Results show learning stabilizes near 80% successful trapping accuracy after approximately 350 episodes.
The first part of our work, improving the accuracy of Aibo kicks, will be addressed as an optimization problem in a framework similar to that used by Kohl. However, the problem of learning a variable distance kick would be tough to characterize with a single optimization function (what distance is optimal?). As a result, model inversion techniques are applied to the problem.
Other past work has modeled the effects of Aibo kicks:
Chernova and Veloso[2] modeled the effects of an arm kick and a head kick by tracking the angle of the ball directly after the kick as well as the distance between the original kick position and the final resting ball location. After collecting data from 480 trial kicks, a regression line is fit, and the kick model is complete. It is then demonstrated that the use of different kicks in different situations can reduce the time taken for an Aibo to score a goal.
Ahmadi and Stone[1] also investigate kick models, this time for use in action planning domain. Unlike the parameterized kick models used by Chernova and Veloso, Ahmadi employs instance based models, in which the resulting ball location of each kick is stored. Using these more complex, instance based models allows the robot to plan more thoroughly about the effects of a given kick in the presence of obstacles or other robots.
Our work can be viewed as an extension to both kick modeling papers. Rather than attempting to model the effects of a fixed number of discrete kicks, we seek to learn a parameterized kick able to deliver any reasonable desired kick distance. Planning approaches, like those above, typically start with a desired kick effect and then choose a kick based on its ability to deliver the desired effect. A paramaterized kick would eliminate the need to pick from a number discrete kicks, each an approximation of the desired effect, and instead give the ability to directly produce the desired kick effect.
Finally, previous work has investigated the process of learning to kick:
Zagal and Ruiz-del-Solar[13] explored the space of fast, reactive ball kicks, those in which no ball re-positioning is required prior to the kick. They use a simulator, UCHILSIM, to model the Aibo and the surrounding environment. The kicking process is decomposed into four postures (configurations of joint angles for each limb), a starting posture, an energy accumulation posture, a ball contact posture, and a follow through posture. Each posture consists of 25 parameters, corresponding to six parameters for each leg and one parameter to control the speed of the joints. A genetic algorithm is used to explore the parameter space, maximizing a fitness function which emphasizes finding a ball kick maximizing ball displacement while maintaining high accuracy in the resulting direction. Notably, all kicks were learned from scratch rather than improving upon existing techniques. The final result of this learning process was a fall kick, qualitatively similar to most powerful kicks in the league at that time.
Cherubini, Giannone, and Iocchi[3] learn two kicks as a part of a larger, layered learning approach focused on learning to attack the goal. Learning initially starts on a simulator, USARSim, and is then ported to the physical robot. The best learned simulator policies become the robot's initial policies, and the robot then employs the same learning techniques to continue to improve its current policy. Learning techniques include a genetic algorithm, Nelder-Mead Simplex (amoeba) algorithm, and a policy gradient algorithm. Both learned kicks were head kicks, consisting first of the robot diving on the ball and hitting it directly with its head and second of the robot again diving on the ball but this time hitting it with a varying head pan. Each kick consisted of nine parameters, corresponding to a sequence of fixed joint positions. Results show progress on the overall task of attacking the goal but are not reported for the subtask of learning to kick.
Unlike previous work on kick learning, our approach has no simulation component. To the best of the author's knowledge, this is the first time a kick has been learned or optimized fully on the physical robots.
Aibo Kicks
Kicking, like all other other complex motion processes, can be reduced to the problem of specifying angles for each joint to assume and maintain for some amount of time. Typically, a complex motion sequence is broken down into a series of discrete poses, or joint angle specifications, and the amount of time to hold each pose. By stringing these poses together and using inverse kinematics to transition from one pose to the next, the Aibo can gracefully execute complex motions.
Hand-coded kicking motions were examined from Austin Villa's Legged League, a team who competed in Robocup since 2003, entering the quarterfinals in 2007 and taking second place in 2008. Of Austin Villa's eleven kicks, the smallest number of poses used was four while the greatest was nineteen, with an average of eight. Typically, to design a kick, each pose must be manually specified and evaluated in the context of the overall motion. Because the Aibo has a total of 18 joints each of which must be determined for every pose, on average a new kick would require a total of 144 joint angle specifications with 8 pose transition timing specifications. Clearly creating a new kick can be a time consuming and complex process.
Of the eleven kicks examined, Austin Villa's Power Kick was the clearly the most powerful and accurate. This kick grasps the ball between the Aibo's front legs and then slams the head down, knocking the ball straight ahead of the Aibo. Consisting of six poses, the power kick takes a total of 114 parameters to fully specify.
From the perspective of machine learning, increasing the number of parameters increases the learning time and complexity of the problem. Previously, Kohl[7] used 14 parameters to characterize a walk and Kobayashi[6] used only two in order to learn the ball trapping. The usual disadvantage of reducing the parameter space is the introduction of human bias. For example, Kobayashi's two parameters for ball trapping, the distance to the ball and the rate of change of this distance (roughly velocity), allow the Aibo to learn effectively when to start lowering the head to catch the ball, but do not allow control over the actual motion of lowering the head. By not allowing this motion to be learned, Kobayashi may be forcing the Aibo to adopt a sub-optimal trapping motion which could limit the overall ball trapping success.
The tradeoff between few parameters and high human bias versus many parameters with slow and complex learning times must be carefully mitigated. The approach used in our work was to start with as little bias as possible and evaluate how well learning was progressing. If little or no progress was observed, the number of parameters would be reduced. Following this philosophy, we originally started learning with all 114 parameters. The problem with this approach proved to be allowing the Aibo to specify joint angles of each leg independently. In general the Aibo is not strong enough to lift the full weight of its body with a single limb, so joint actuators were frequently unable to fulfill individual joint requests because there was simply too much weight for the actuator to lift. This lead to unnecessary stress and resulted in an Aibo burning out the actuator for its front left rotator joint.
To address this problem, the kick was re-parameterized to take advantage of the Aibo's symmetry. This forced the three joints in the front left leg to mirror those of the front right; the same was true of the back legs. Additionally, the two joints in the tail were assumed to be useless and eliminated from the learning process. This reduced the parameter space from 18 to 10 joint specifications per pose for a total of 66 parameters, including timings between poses. It seems the symmetry constraint largely solved the problem of actuator stress, as there have been no more broken Aibos, while introducing little human bias. While total number of parameters is still significantly greater than attempted in previous work, learning remains effective.
The Learning Process
Using the kick parameterization described above, we attempt to optimize all 66 parameters with respect to the power of the kick. Power was equated to kick distance for the purpose of this project. In order to make the learning process as automatic as possible, a ramp was constructed to return the ball to the Aibo after each kick:
 |
The learning process consisted of the Aibo testing a new kick, receiving information of the distance up the ramp the ball traveled, and being re-positioned for the next kick. After each kick, a human was required to relay the distance of the kick and reposition the Aibo for the next kick. Making this process fully autonomous proved quite difficult for several reasons: first, the process of kicking is quite violent and often unpredictable. During the kick motion sequence, it was common for the Aibo to either fall over or the fumble the ball behind itself, both events making it hard to recover and reposition the ball for the next kick. Second, as a result of the carpet covering the ramp, the ball didn't always return from the kick and would occasionally get stuck at the apex of its path. This could have been resolved with a steeper incline but that would have lead to less informative distance feedback after every kick. Finally, it would have been problematic for the Aibo to autonomously estimate kick distance because many kicks end with the Aibo's head (and sometimes body) facing in a different direction than the path of the ball and would require extremely fast visual re-acquisition of the ball and distance estimation all before the ball reached its apex. Despite the dependence on human assistance, the ramp system was quite efficient, yielding approximately 500 kicks over the duration of a single battery charge, or about one hour.
Two different methods for estimating the distance of a kick were employed at different points in the project. Initially, distance was estimated by measuring the time difference between the end of the kick and the return of the ball. This was calculated internally on the Aibo using a timer. On a friction-free surface, this metric would have been correct, but due to the friction between the ball and the carpet, strong kicks were found to take nearly the same amount of time to return as weak ones. To resolve this problem, ten distance markers were placed along the ramp in 20cm intervals. After each kick, the distance of the ball, as measured by which marks it had passed, was reported to the Aibo in the form of a text message. The second metric proved more reliable than the first, but due to its late discovery not all experiments were able to be redone.
Finally, the slope of the ramp was adjustable by changing the height of the object the far end was resting upon. An optimal slope was found through trial an error, guided by the principle that the ramp should be as low as possible so long as the Aibo was unable to kick the ball off the far end.
Machine Learning Algorithms
Two different machine learning algorithms were employed. The first, hill climbing, was used for its simplicity and robustness in the presence of high numbers of parameters. The hill climbing algorithm starts with an initial policy π consisting of initial values for all of the parameters and generates one or more additional policies {R1,R2,...,Rt} in the parameter space around π. The policies are then evaluated and the best is kept as the initial policy in the next iteration. Because Hill Climbing is little more than a guess and check algorithm, it can safely be used in the presence of high dimensional parameter spaces, making it ideal for both tuning and learning high dimensional kicks.
Hill Climbing Pseudocode:
π ← InitialPolicy
while !done do
{R1,R2,....,Rt} = t random pertubations of π
evaluate({R1,R2,...,Rt})
π ← getHighestScoring({R1,R2,...,Rt})
end while
Policy Gradient Algorithm was chosen because it has been shown previously to be effective at learning Aibo walk and grab. This specific variant of general policy gradient learning techniques (Sutton et al. 2000; Baxter & Bartlett 2001) seeks to estimate the gradient of the objective function by sampling policies in the vicinity of the initial policy and estimating the partial derivative for each parameter. After the gradient has been estimated, the new policy is shifted in the direction maximizing the objective function. Essentially, we estimate if increasing, decreasing, or holding constant each parameter {+ε,-&epsilon,+0} is favorable by computing an average score for all policies Ri who increase or decrease dimension n. After determining the favorable direction to shift each parameter, the new policy is created by adding an adjustment vector A to the current policy. Finally, A is normalized by a scalar step size η so the adjustment will remain a fixed size each iteration.
Policy Gradient Pseudocode:
π ← InitialPolicy
while !done do
{R1,R2,....,Rt} = t random pertubations of π
evaluate({R1,R2,...,Rt})
for n = 1 to num_parameters do
Avg+ε,n ← average score for all Ri that have a positive pertubation in dimension n.
Avg+0,n ← average score for all Ri that have a zero pertubation in dimension n.
Avg-ε,n ← average score for all Ri that have a negative pertubation in dimension n.
if Avg+0,n > Avg+ε,n and Avg+0,n > Avg-ε,n then
An ← 0
else
An ← Avg+ε,n - Avg-ε,n
end if
end for
A ← A⁄|A| * η
π ← π + A
end while
Unfortunately, the policy gradient algorithm is more sensitive to high dimensional learning in that it requires many policies be evaluated before it can confidently estimate the gradient. In general, the number of policies evaluated per iteration of the algorithm should be greater than the number of parameters being learned.
Implementations and pseudocode for both Hill Climbing and Policy Gradient were re-used from Nate Kohl's work on quadruped locomotion[7].
Results
Both Hill Climbing and Policy Gradient Algorithms proved effective for learning how to optimize kick power. Figure 1 shows the results of running the Hill Climbing Algorithm for only 27 iterations starting from an motion sequence unable to even propel the ball forwards.
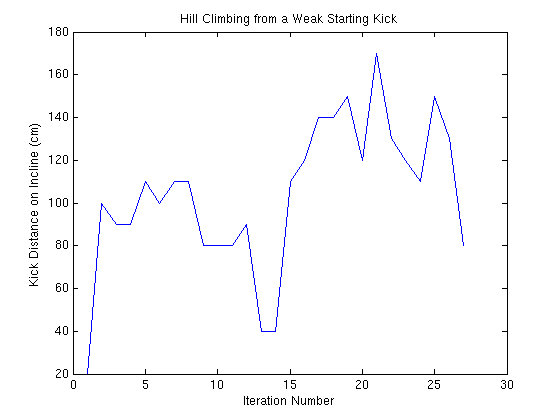 |
This experiment was run with five policies evaluated in each iteration of hill climbing, where each policy was scored by the average distance of two kicks generated by that policy. The initial policy started with a distance score of zero, as it was unable to kick the ball forwards. In just a few iterations a working kick is discovered by random chance and generally optimized throughout the rest of the run. Amazingly, after only 21 iterations, the kick is powerful enough to near the end of the 200cm ramp. The large fluctuations in kick distance results from the unreliable nature of the nose kick learned throughout this experiment. While occasionally quite powerful, this kick proved far too inaccurate for further consideration; the example serves only to demonstrate that kicks can be learned quickly and effectively using Hill Climbing.
The Policy Gradient Algorithm was influenced by the high dimensionality of the learning problem. As previously mentioned, in order to reliably estimate the gradient of the optimization function, a number of policies greater than or equal to the number of parameters being learned should be used. With 66 parameters, this would have taken a prohibitive amount of learning time for each iteration. We decided to place an emphasis efficient learning and chose to evaluate only ten policies each iteration with each policy scored according to the power of one kick generated by that policy. Policy Gradient was run for 65 iterations over the course of one battery charge. The initial policy used was Austin Villa's Power Kick. Figure 2 plots how different the current policy is with respect to the initial policy and the score of the current policy (as measured by the amount of time taken for the ball to return from a kick -- the initial metric).
 |
From this graph we can glean several pieces of information. First, it's clear that Policy Gradient is not stuck in some local optima in the space around the Power Kick. Instead, the policy continues to move and evolve in a process loosely resembling punctuated equilibrium. In general, while there are occasional spikes in score (one kick went off the far end of the ramp), there is little to no sustained improvement in overall score throughout the run. In essence, it seems that PG showed no real trend towards convergence but was able to aptly explore the parameter space while maintaining a consistent score. Indeed, throughout the course of the run several different types of kicks were observed. The first phase of kicking resembled the original power kick. After that, the kick evolved into a chest hit and ceased to use the head at all. Next, the head was reintroduced in conjunction with the chest, and finally the kick evolved into only using the head -- similar to the nose kick previous optimized.
While Policy Gradient did not converge on any single kick within 65 iterations, it did discover some interesting and powerful kicks along the way. For example the single kick powerful enough to make it off the end of the ramp, the one with a 9500ms return time, turned out to be a purely chest kick. This kick was subsequently selected and tuned further via Hill Climbing as shown in figure 3.
 |
After completing 18 rounds of Hill Climbing, the learned kick was evaluated against the Power Kick. Originally the evaluation was done by benchmarking the distance and accuracy of each kick over 50 trials on a single Aibo. In this context, the learned kick showed significant improvements in both distance and accuracy compared to the power kick. However, it was soon discovered that the power of any kick depends heavily on Aibo performing that kick. Therefore, it was concluded that for any reasonable comparison, each kick would need to be evaluated on multiple Aibos.
The Power Kick was evaluated against the best Learned Kick on flat ground with five different Aibos and five trials of each kick per Aibo. For each trial, three distances were recorded: the resting X-Distance of the ball, the resting Y-Distance of the ball, and the Y-Distance of the ball as it passed the 200cm mark (recall the 200cm mark had special significance for passing as it was the longest possible passing distance). These metrics are graphically displayed in Figure 4.
 |
 |
| Metric | Power Kick | Learned Kick | Difference |
| Longest Kick | 491cm | 628cm | 137cm |
| Average X-Distance | 290.2cm | 333.56cm | 43.36cm |
| Average Y-Distance | 63.2cm | 78.16cm | 14.96cm |
| Percentage to Cross 200cm Mark | 72% | 100% | 28% |
| Percentage Successful Passes* | 36% | 28% | -8% |
| Variance of 200cm Y-Displacement | 501.77 | 877.53 | 357.76 |
Figure 5 shows the resting locations of all 25 power and learned kicks and Table 1 assesses each type of kick along six dimensions. The two kicks are quite close in many respects, with the learned kick taking the slight (although not statistically significant) advantage in power (X-Distance) while the power kick proved slightly more accurate (Average Y-Distance and Variance @200cm). Notably, the learned kick was able to always move the ball at least 200cm and incidentally produced a kick so powerful it was stopped only after hitting the far wall of the room, a distance of 628cm, or over 20 feet!
 |
As figure six demonstrates, the performance of the Power and Learned kicks depends highly on the Aibo. In fact, the learned kick seems complementary to the power kick in that Aibos who are weak at one are typically strong at the other. Rather than designing a single kick for a whole Aibo team, perhaps each Aibo should have the option to evaluate and choose its favorite kick. If this were the case, then none of the five Aibos would kick less than 350cm on average.
Variable Distance Kick
While a powerful and accurate kick might be able to reliably reach a target Aibo, we speculate that overpowered passes are harder to receive than passes with a predictable, and more moderate, velocity. Accordingly, we seek to design a kick which gives the passing Aibo control over the power and distance of the hit.
Rather than learning a new kick, or possibly many new kicks -- one for each desired distance, it was decided to investigate how changes in the timings between poses on UT's power kick affected the overall kick distance.
Austin Villa's power kick consists of 6 poses with 6 pose transition times. The third pose of the six was identified as the "hit" pose, or the pose in which the Aibo makes contact and propels the ball forwards. The initial kick provides 24 frames (192 milliseconds) to transition into this "hit" pose, but it was observed that varying the amount of time allotted to this pose greatly affected the power of the kick.
 |
Distances of power kicks on flat ground were recorded for number of frames in "hit" pose ranging from 0 to 100, with the Figure 7 showing the interesting part of this range. Each distance point is the average of the distances of three kicks. Figure 7 shows the distances plotted as a function of the number of frames in the "hit" pose, as well as the standard deviation of the three kicks composing each distance point.
After distance data was collected, a quadratic was fit to the points (shown in blue on Figure 7). In order to invert the model, it was necessary to solve for the number of frames as a function of the desired kick distance. This yielded two equations:
x = (sqrt(15)*sqrt(87437-220*y)+885)/33.
Where x is the number of frames in "hit" pose and y is the desired distance. The top equation corresponds to the left side of the quadratic while the bottom is the right side.
The standard deviations inform us that the left side of the quadratic has lower variance and should be preferred over the right side whenever possible. As a result, a simple variable distance kick was designed which uses the top equation if the desired kick distance is between 160cm and 398cm (the maximum of the quadratic function) and the right side for all other distances.
In controlled tests the variable distance kick seemed to work quite well, however the true test for this kick will be whether or not if proves useful for making successful passes.
Future Work and Conclusions
There is much future work to be done. Meaningful evaluations of both the learned kick and the variable distance kick need to be performed in the context of the Robocup passing challenge. All experiments using the older metric for estimating kick distance should be redone. Policy Gradient and Hill Climbing should be run for more iterations than currently documented -- ideally until convergence. Additionally, PG has yet to be applied to the task of learning a kick starting from a weak initial policy. Finally, more complex environments could be created to increase the autonomy of the learning process.
In this work we demonstrated the efficient and effective learning of unique kicks whose power and accuracy rival that of the best known hand coded kicks. More importantly, these kicks were learned in a way that required minimal task-specific engineering of the parameter space. In addition, we created a parameterized kick capable of propelling the ball a requested distance. The author believes that both of these contributions will prove useful to the Robocup passing challenge as well as to the larger problem of winning at robot soccer.
References
- ^ Ahmadi, M., & Stone, P. Instance-based action models for fast action planning. In RoboCup-2007: Robot Soccer World Cup XI, 2007.
- ^ Chernova, S., & Veloso, M. Learning and using models of kicking motions for legged robots. In Proceedings of International Conference on Robotics and Automation (ICRA), 2004.
- ^ Cherubini, A., Giannone, F., & Iocchi, L. Layered learning for a soccer legged robot helped with a 3D simulator. In RoboCup 2007: Robot Soccer World Cup XI, 2007.
- ^ Fidelman, P., & Stone, P. Layered learning on a physical robot.
- ^ Fidelman, P., & Stone, P. The chin pinch: a case study in skill learning on a legged robot. In Gerhard Lakemeyer, Elizabeth Sklar, Domenico Sorenti, and Tomoichi Takahashi, editors, RoboCup-2006: Robot Soccer World Cup X, Lecture Notes in Artificial Intelligence, pp. 59-71, Springer Verlag, Berlin, 2007.
- ^ Kobayashi, H., Osaki, T., Williams, E., Ishino, A., & Shinohara, A. Autonomous learning of ball trapping in the four-legged robot league. In RoboCup 2006: Robot Soccer World Cup X, 2006.
- ^Kohl, N., & Stone, P. Machine learning for fast quadrupedal locomotion. In The Nineteenth National Conference on Artificial Intelligence, 2004.
- ^ Kohl, N., & Stone, P. Policy gradient reinforcement learning for fast quadrupedal locomotion. In Proceedings of the IEEE International Conference on Robotics and Automation, 2004.
- ^ Mahdi, A., de Greef, M., van Soest, D., & Esteban, I. Technical report on joint actions for an aibo team.
- ^ Saggar, M., D'Silva, T., Kolh, N., & Stone, P. Autonomous learning of stable quadruped locomotion. In RoboCup-2006: Robot Soccer World Cup X, 2007.
- ^ Stone, P., Veloso, M. Layered learning. In Machine Learning: ECML 2000, 2000.
- ^ Technical Challenges for the RoboCup 2007 Legged League Competition, link
- ^ Zagal, J. C., & Ruiz-del-Solar, J. Learning to kick the ball using back to reality. In RoboCup 2004: Robot Soccer World Cup VIII, 2004.