Token Caching for Diffusion Transformer Acceleration arxiv:2409.18523
2024-10-16
Overview
Motivation & Key Contributions
- Motivation:
- Diffusion generative models are slow because of high computational cost, arising from:
- Quadratic computational complexity of attention mechanisms
- Multi-step inference
- Diffusion generative models are slow because of high computational cost, arising from:
- How to reduce this computational bottleneck?
- Reduce redundant computations among tokens across inference steps
- Key Contributions:
- Which tokens should be pruned to eliminate redundancy?
- Which blocks should be targeted to prune the tokens?
- Which timesteps should be applied caching?
Token Cache (System Overview)
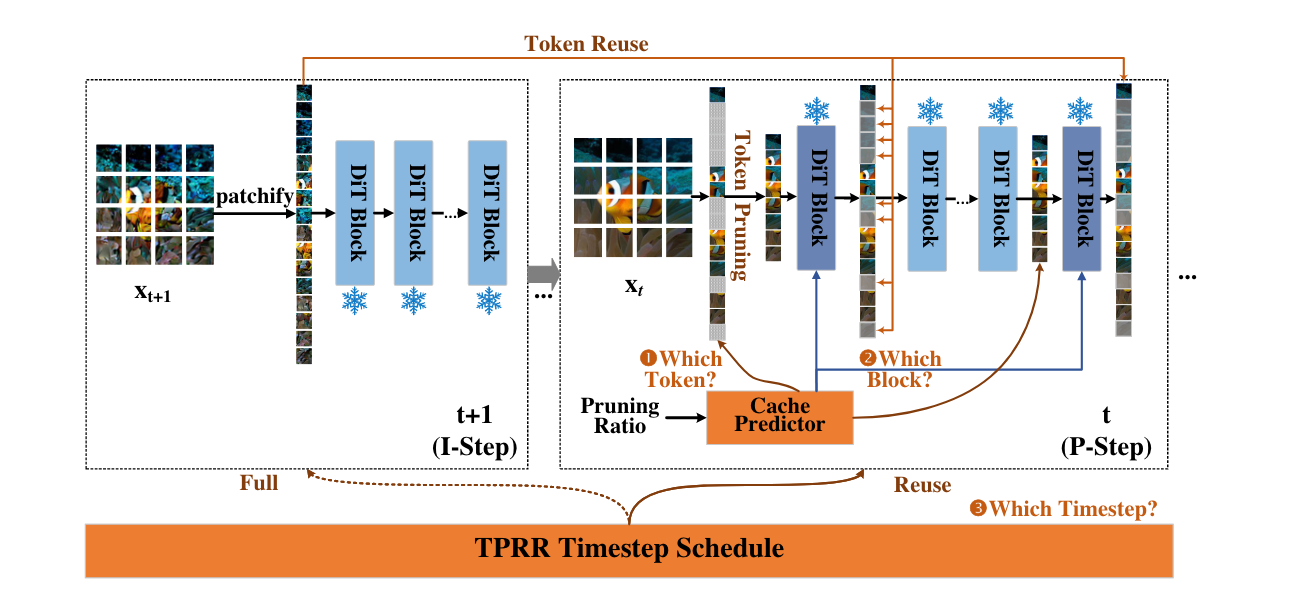
Figure 1: Overview of TokenCache
TokenCache
Use a small learnable network g_{θ} dubbed Cache Predictor Lou et al. (2024) to predict the importance of the tokens w^{t}_{l} = g_{θ}(l, t) \in \mathbf{R}^{n}, and prune the tokens based on their relative importance.
How to learn g_{θ}?
- Instead of predicing binary importance [0,1], use interpolation to “superpose” pruned and non-pruned token states
- Interpolated states are gerenated via: \hat{z}^{t}_{l+1} = z^{t}_{l} + \hat{f}_{l}(z^{t}_{l})
\hat{f}(z^{t}_{l}) = \textcolor{#800080}{w^{t}_{l} ⦿ f_{l}(z^{t}_{l})} + \textcolor{#008080}{(1 - w^{t}_{l}) ⦿ f_{l}(z^{t+1}_{l})} where diffusion transformer contains total number of L network blocks, with a total of T inference timesteps and z^{t}_{l} \in \mathbf{R}^{n \times d} denotes input to block f_{l} at timestep t
🔍 Optimization Objective
ℒ_{\text{mse}} = 𝔼_{t, z^{t}_{L+1}, \hat{z}^{t}_{L+1}} [‖ z^{t}_{L+1} - \hat{z}^{t}_{L+1}‖^{2}_{2}]
Cache Predictor (Visualized)
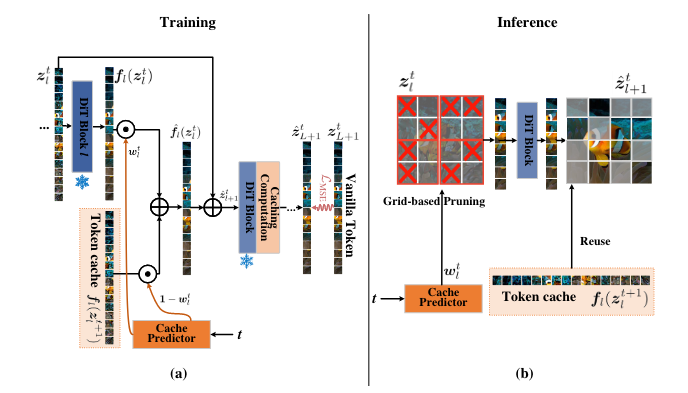
Figure 2: Overview of Cache Predictor
Two-Phase Round Robin Timestep Scheduler
Token Caching inherintly adds errors into the samplingtrajectory.
How to mitigate errors?
- Perform independent (no-cache) steps (I-Steps) after K prediction/caching steps (P-Steps)
- K = Caching Interval
How to choose K?
- Token correlations vary across timesteps.
- Higher correlations among tokens across early timesteps
- Lower correlations among tokens across later timesteps
- Token correlations vary across timesteps.
TPPR
- Phase-1 employs larger caching interval K_1
- Phase-2 employs smaller caching interval K_2
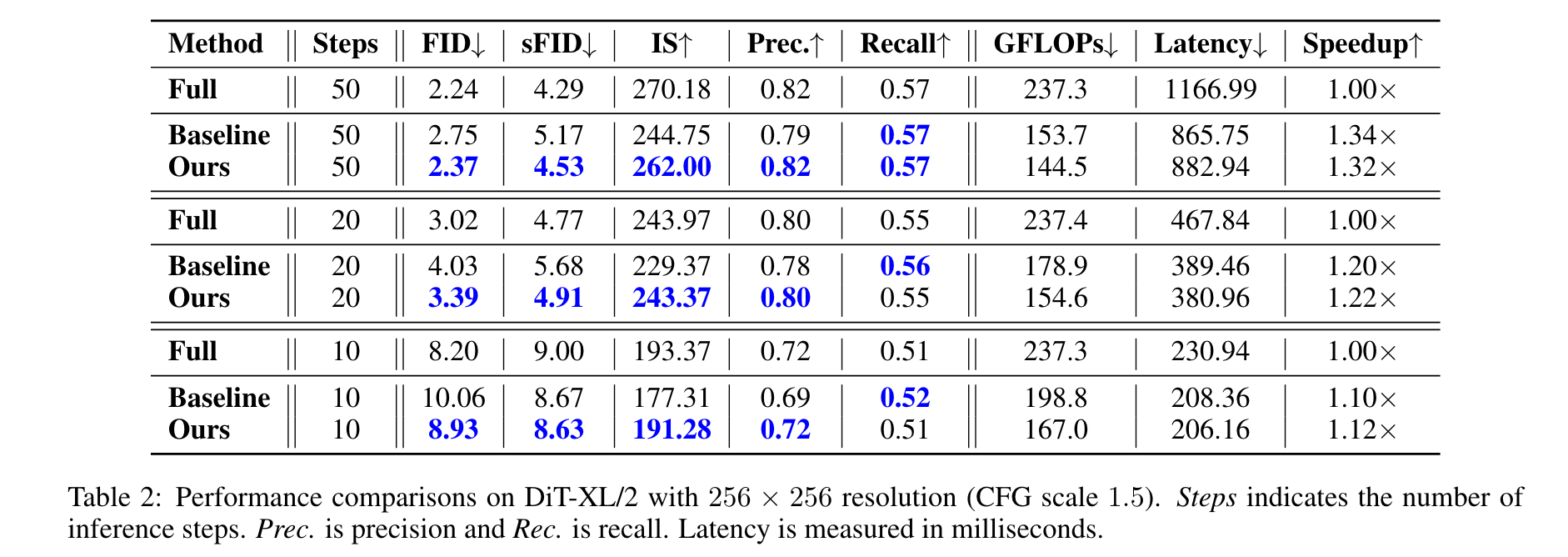
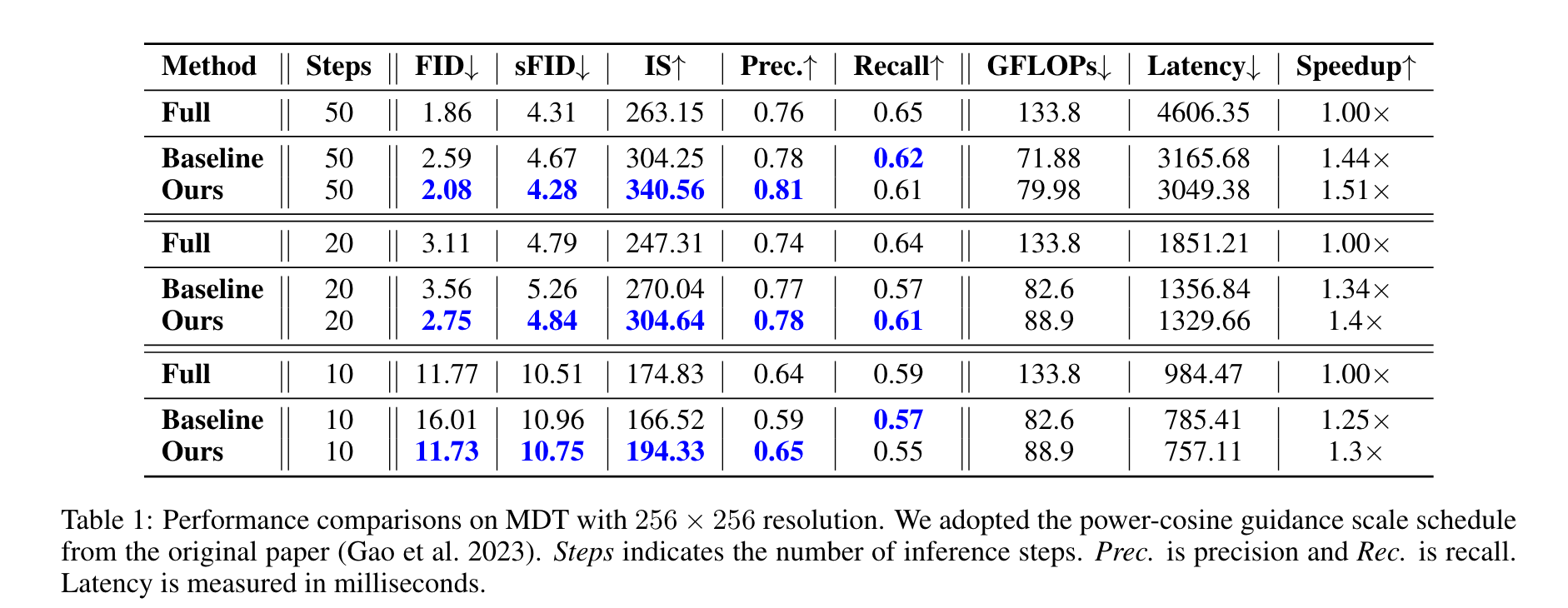
Experimental Results