CS 343 Artificial Intelligence
Homework 4: Machine Learning and Natural Language


Due: May 7, 2009

  1. Consider a concept learning problem described using the given features:
    For each of the following two different training sets, show the consistent hypothesis learned, if any, by the maximally specific conjunctive learning algorithm. If no consistent conjunctive hypothesis is learnable, clearly state this and explain why.

    Training Set 1:

    Training Set 2:


    What is the total number of possible binary functions over this instance space?
    What is the total number of semantically distinct conjunctive hypotheses over this instance space (assuming negation is not allowed)?

  2. Using the same features as in the previous problem, show the decision tree learned by the ID3 algorithm from the training set:
    Explicitly show the gain of each feature at each choice point. If there is a tie in gain, prefer the feature first in the list: (size, color, shape).
    Below are the relevant formulae:
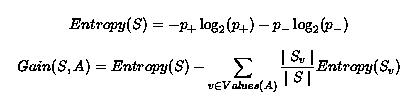
  3. Given the following context-free grammar, draw trees for all parses produced for the sentence: ``Guard tests like gold.'' Under each tree, briefly paraphrase in English the meaning of each parse as best you can and circle the most likely interpretation. 
    S -> NP VP, S -> VP,
NP -> Adj NP,  NP -> N, NP -> NP PP,
VP -> V, VP -> V NP, VP -> VP PP
PP -> Prep NP,
Prep -> like,
N -> guard, N -> gold, N -> tests,
V -> guard, V -> tests, V -> like,
Adj -> gold,  Adj -> guard
  4. Given the simple PCFG in the domain of air travel given on slide 70 of the slide packet on NLP, show all of the parse trees for the sentence "I prefer the flight through Houston on NWA" and compute the probability of each. Also compute the probability that the grammar generates this sentence P("I prefer the flight through Houston on NWA"). Finally, compute the labeled precision, recall, and F1 evaluation score for each incorrect parse tree when compared to the correct parse.