CS 351 Lisp and Symbolic Computation
Homework 4: Prolog
Due: April 25, 2000 (3:15 PM)
The Prolog code from Norvig is in /u/mooney/cs351-code/prolog.lisp The
file family-rules.lisp contains rules and data for the family relations
domain. The file hw4-utilities.lisp contains an addition to the Prolog
interpreter in the form of an alternate query macro, ?-* that
automatically generates all answers to a query without requiring user
interaction.
Make sure you compile and load all of the needed auxiliary files. You should
submit the final commented code you write electronically using turnin. Just submit the Lisp code you write or
change and assume it will be loaded on top of the existing utilities and Prolog
interpreter. Include in the file your edited version for a complete set of
family rules (do not assume that family-rules.lisp has been
loaded since these should be replaced by your edited rules). Discussion of any
questions below should be given as comments in the file at an appropriate
point.
Extending the Interpreter
Add negation as failure (e.g. (not (parent ?x ?y))) to the incremental
Prolog interpreter. Use this to fix the problem in the family rules that
someone is considered their own sibling.
More Family Rules
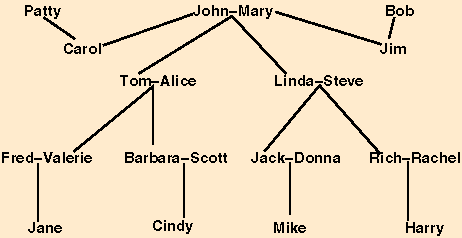
Add rules to handle the following family relationships: second-cousin,
cousin-once-removed, step-father, step-mother, step-son, step-daughter,
step-brother, step-sister, half-brother, half-sister, and blood-relative. For
your convenience, a graphical picture of the family tree for the data given in
family-rules is included. You can use the ?-* macro to directly
retrieve all answers to the queries in the list questions3 given in
family-rules. A trace of my rules running on these queries is in
hw4-trace. Remember to call (clear-db) to clear the
database of rules before loading your modified version.
Logic Programs
Write logic programs for (subset ?x ?y) (X is a subset of Y) (union
?x ?y ?z) (Z is the union of X and Y) and (intersection ?x ?y ?z)
(Z is the intersection of X and Y). Assume sets are represented as lists,
inputs sets will not contain duplicates, and output sets should not contain
duplicates. You may want to use negation as failure in your programs. Can
your programs effectively compute inputs from outputs, e.g. compute all
subsets of a set or all pairs of sets whose union produces some set? If it
can't, it's O.K., but you have to explain why this is difficult.
