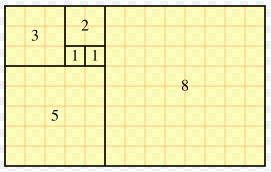
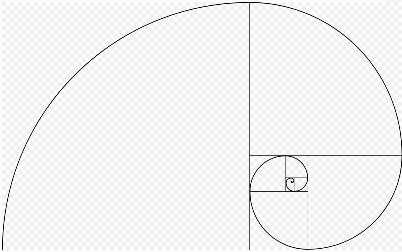
Leonardo of Pisa, known as Fibonacci, introduced this series to Western mathematics in 1202:
| F(0) | = | 0 |
| F(1) | = | 1 |
| F(n) | = | F(n - 2) + F(n - 1) , where n > 1 |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610


The ratio between successive Fibonacci numbers approaches the golden ratio &phi = ( 1 + &radic 5 ) / 2 = 1.618034... .