Copyright © 1994 by IEEE.
Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works must be obtained from the IEEE.
This article appears in Proc. 9th Knowledge-Based Software Engineering Conference (KBSE-94), pp. 39-47, Monterey CA, Sept. 1994, IEEE Computer Society Press.
Computer equipment used in this research was provided by Hewlett Packard.
The ability to combine separate reusable software components to form a complete program is necessary for effective software reuse. Views provide a clean, flexible, and efficient mechanism for combining reusable software components. A view describes how an application data type implements features of an abstract type; it provides a bidirectional mapping between a generic concept and a particular implementation of that concept. Parameterizing a generic procedure by means of views allows a single copy of the procedure to be specialized for a variety of application data types and target languages. Both composition of views and multiple views of the same data as different abstract types are often required. Automated support makes it easy to create views and to generate specialized code for an application in a desired target language. These techniques have been implemented. Examples are presented that illustrate combination of components through views to specialize a generic procedure and to instantiate a software framework.
Reuse of software has the potential to reduce programming cost, increase the speed of software production, and increase reliability. However, it is unlikely that a given piece of software will be exactly what is needed for a new application. Reuse therefore means reuse of ``most of'' or ``the essence of'' the reused software, while customizing it to fit the present application.
In most programming languages, fundamental design decisions (such as the kinds of data structures that are used) become distributed throughout the code, so that the effects of a single decision appear in many places [balzer85]. This makes modifying software for reuse by editing the code itself both difficult and error-prone. On the other hand, if a version of a reusable software component is made for each combination of decisions, there will be a combinatoric number of components; it will be difficult to maintain all the components and difficult for a potential user to find the right component. For example, the Booch component set [booch87] contains over 500 components; Batory [batory93] has identified these as combinations of a smaller number of design decisions.
All engineering disciplines make use of well-understood components and form systems by combining components. Computer science has its components too, such as abstract data types and algorithms. However, combining software components to form a system often requires custom-crafting of each component so that they will fit together. For effective software reuse, there must be an ability to combine separate software components, each of which is derived from an individual generic component, to form a complete software system. If this can be done, the number of components to be stored, maintained, and understood by potential users will be the total number of concepts, rather than the combinatoric product of the numbers of options for each decision. To make such an approach work, it must be possible to state design decisions in a single place and to propagate those design decisions to the code automatically. There must be a flexible way to interface components, so that two components can be interfaced without having to be designed to be interfaced ab initio. There must be flexibility to use arbitrary data formats: in real applications, a single data set often plays multiple roles; if reusable procedures restrict the form of data, these restrictions inevitably will conflict. The use of heterogeneous data sets from different sources and with different representations will become more common as communication across networks increases.
In this paper, we describe how views allow reuse and combination of multiple software components to form a single program. Views allow generic procedures, which are written in terms of abstract data types, to be specialized to operate directly on application data. A single copy of a generic procedure can work with a variety of application data representations and can be used to generate application code in multiple target languages. Examples will be presented to illustrate how views allow specialization of generic procedures for applications, with target code being generated in Lisp or C.
Section 2 describes views and the way in which generic procedures are specialized by compilation through views. Section 3 describes a simple example, in which views relate the concept of a polygon to a variety of possible data structures that could represent polygons. Section 4 describes a generic application program that produces a keyword in context (KWIC) index; it shows how views can be used to plug software and data components into this software framework to generate customized KWIC index programs. The final sections discuss related work and conclusions.
The programming tools described in this paper are based on the GLISP language and compiler. GLISP [novak:glisp,novak:gluser,novak:tose92] is a high-level language with abstract data types that is compiled into Lisp. It has a data structure description language that allows Lisp data structures to be specified, and it can be extended to describe data structures in other languages. GLISP also has a class structure with inheritance and messages, analogous to that of object-oriented programming. A ``function call'' on a data object is interpreted as a structure access if the function name is the name of a substructure of the object, or as a message if a message with that name is defined for the object. When the type of an object is known, a ``message'' to the object can be handled specially by the compiler:
A view [novak:glisp][novak:kbse92][novak:views93] is a GLISP type that specifies how an application type implements the features of an abstract type. An abstract type is considered to be an abstract record containing a set of basis variables. An application type may implement this set of basis variables, but with certain changes, e.g. different data structure, different variable names, different units of measurement, or even different sets of variables (such as representing a vector using polar coordinates rather than Cartesian coordinates). A view encapsulates the application type, hiding its names, and presents an external interface that consists of the basis variables of the abstract type. The view not only allows basis variables to be ``read'', but allows them to be ``written'' as well. The view must simulate the abstract record by maintaining two properties:
In practice, the above definition of a view is relaxed slightly:
A view type that implements an abstract type using an application type, while maintaining the storage and independence properties, may be complex. For example, a view of an application type as a line-segment may be over 60 lines of code. Therefore, coding view types by hand is not something that average users should have to do. We have developed tools that make it easy for the user to specify a view by indicating correspondences between the application type and the abstract type. These tools have graphical interfaces that are fast and easy to use.
The first tool, VIEWAS [novak:kbse92], is useful for making data structure views, e.g., viewing an application type as a linked-list or avl-tree. In these cases, the mappings between the application type and abstract type are generally one-to-one ( e.g., a pointer in one type corresponds to a pointer in the other type), but the view types that must be produced are detailed. VIEWAS uses type filtering to eliminate unsuitable candidates for matching. If only a single choice remains after type filtering, it is chosen automatically; otherwise, menus are presented so that the user can make the choice.
A second tool, MKV (for ``make view'') [novak:views93] (Fig. figmkv), is useful for making mathematical views. MKV uses a graphical interface, on which it presents a menu of the data available in the application type together with a diagram associated with the abstract type. The diagram contains sensitive spots or ``buttons'' that are associated with variables. The set of variables that is presented is a complete set, intended to include all reasonable ways of representing that kind of object. The user specifies a correspondence between a button and a field of the application data by selecting each with the mouse; a line is then drawn between the two to indicate the correspondence. Equations associated with the abstract type are solved by symbolic algebra as correspondences are specified. Finally, a view type is constructed that includes appropriate messages to ``read'' and ``write'' each basis variable and to create a new object given a set of basis variable values. In addition, when certain properties of the abstract type can be computed more efficiently from the application type than by using the generic procedures in terms of the basis variables, messages for those properties are included. For example, in a polar coordinate representation of a vector, the magnitude of the vector is available directly from the polar form. The algorithms used by MKV are given in [novak:views93].
This section describes how a user obtains specialized versions of generic algorithms for use in an application program. We assume that the user is a programmer of average ability; while the generic procedures and views may be complex, the system should hide this complexity and should be fast and easy to use. In addition, only a modest amount of learning should be required to use the system; the system should communicate with the programmer in familiar terms.
The steps involved in obtaining a specialized version of a generic procedure are as follows:
Each of these steps is either simple, or has an automated tool to make it easy to perform.
Mathematically, a polygon can be represented as a sequence of points in a plane. There are several generic procedures associated with polygons that one might wish to reuse: perimeter of a polygon, area, center of mass, testing whether a given point is inside a polygon, etc. Some of these are simple, but others may not be immediately obvious or may have subtleties that must be handled properly in order for an implementation to be correct. It is clear, therefore, that reusing such procedures would be better than rewriting them from scratch.
In an application, data that can be viewed as a polygon might be represented in many different ways. The application data will contain some sequence of things, each of which can be viewed as a point. There are many possible kinds of sequences (array, linked list, circular linked list, tree, etc.) and many ways in which a point might be represented (Cartesian coordinates, polar coordinates, position relative to some other point, chain code, etc.). The challenge is to be able to reuse a single copy of each polygon procedure for any legitimate representation of a polygon.
Library procedures might exist for computing features of polygons. Our viewing techniques [novak:tose92] or a method such as IDL [lamb83] could be used to generate a procedure to translate an existing data set and materialize it as a data set suitable for use with a fixed library procedure. However, translating data in order to use a procedure may be unsatisfactory. At best, it requires time to perform the translation and space to store the translated data (which likely will be discarded after the procedure is called). If the procedure modifies the data set, the modified data will have to be translated back to the original form and merged into the existing data set. These steps at best detract from the benefit of reuse, and at worst may be more costly than writing a custom version of the procedure from scratch.
A better solution is to specialize a generic procedure so that it operates directly on the original data. Translation of the data will be done ``on the fly'' so that only a few pieces of data are translated at any given time. If changes are made to the data, the original data set will be modified directly. Because symbolic optimization and partial evaluation are performed on the generated code, the data translation can often be folded into other operations, so that there is no translation cost in either time or space.
In our implementation, the mapping between application data and the abstract concept of a polygon is represented as two component views and a derived view:
In writing generic procedures, we try to follow the principle that each concept (abstract data type or generic procedure) should be represented only once, at the most abstract level possible; generic procedures should reuse other generic procedures in their definitions when possible. Each of the generic polygon procedures reuses several others as components:
The specialization of a generic polygon procedure is illustrated as follows. We assume that the user has a predefined data structure that represents a polygon and that the user wants a version of a generic polygon procedure that is specialized for that data structure. The procedure to compute the area of a polygon will be used as an example. We assume that the user's data structure is a circularly linked list formed from the following C structure:
typedef struct polyb {
float r, theta;
struct polyb * next;
} POLYB;
The equivalent GLISP declaration for this data structure is:
[It would be easy to create this declaration automatically
by parsing the C declaration.]
(polyb (crecord polyb
(r real)
(theta real)
(next (^ polyb)) ) )
In order to reuse the polygon procedures, it is necessary to make two views: a view of the given data as a sequence, and a view of the sequence element as a point. Two different tools make it easy to create these views. VIEWAS [novak:kbse92] can make the view of the data as a circularly linked list:
(viewas 'circular-linked-list 'polyb) Choice for LINK = NEXT POLYB-AS-CLLVIEWAS determines that the only possibility for the LINK of a circularly linked list is the pointer stored in the NEXT field, so it makes that choice automatically and constructs the view types. This view makes available the iterator associated with circularly linked lists.
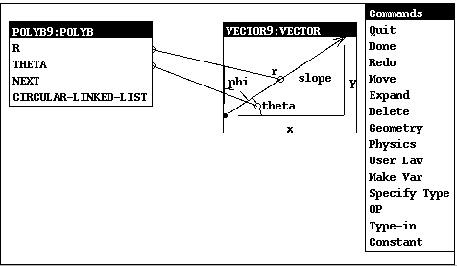
The second view that is needed is a view of the data as a point. The user uses MKV (``make view'') [novak:views93] to make this mathematical view, as shown in Fig. 1:
(mkv 'vector 'polyb)

Fig. 1: Viewing a polyb as a vector
Finally, a polygon datatype is needed to combine these views. [Automated support for making this declaration has not yet been implemented since the declaration is short.]
(polybc (p polyb)
prop ((seqview ('g0023))
(pointview ('vector))
(g0023 ((circular-linked-list p))))
supers (polygon) )
Once the appropriate views and declarations have been made, all of the generic procedures associated with a polygon are available by specialization. If the user wants a procedure to compute the area of a polygon, in a form that can be included with other code, a small function that requests the area will cause such a specialized function to be created when it is compiled:
(gldefun t1 (p:polybc) (area p))When this function is compiled, a specialized version of the function for computing the area, polygon-area-b-3, will be produced. The desired code is obtained by requesting translation of the specialized function into C:
(gltoc 'polygon-area-b-3)The resulting C procedure, about 47 lines, is shown in the Appendix. This example illustrates how views, produced with the automated tools we have developed, make it easy to derive specialized versions of generic procedures. The generic functions associated with polygons have been specialized and tested on a variety of sequences (arrays, linked lists, circularly linked lists) and a variety of representations of points (Cartesian, polar, cities with UTM coordinates, locations relative to cities such as ``40 miles NE of Austin'', chain code, etc.). By mapping characters to locations on a keyboard, a string can be viewed as a polygon: does the polygon represented by the string "car" contain the letter d? A single copy of each generic procedure can be specialized for any of these representations of a polygon.
This example illustrates how generic procedures can be specialized so that they operate on application data whose format is independently specified. Obtaining the specialized procedures is fast, and only a small amount of user input is required.
A software framework is a collection of related software components (data sets and procedures) that perform a certain task. By instantiating the software framework with different components, a specialized version can be obtained. This section describes how a software framework for a Key Word in Context (KWIC) index can be instantiated by using views to connect the framework and components. By using views to describe the user's data and by reusing generic procedures and existing data sets, a specialized KWIC program can be obtained with much less work that would be required to write one from scratch.
A KWIC index is produced in the following way. A sequence of records, e.g. representing articles, is input. Each record contains a title (sequence of words) and some other information. An index is produced showing each key word from the title surrounded by part of its context, together with other information extracted from the record; this index is sorted alphabetically by keyword. A (truncated) example of such an index is shown in Fig. 2.
Some Philosophical Problem McCarthy 1969
dels of Physical Mechanisms deKleer 1980
tion of Physics Problems by E Chi 1981
Physics Halliday 1978
tion in Physics Larkin 1981
Fig. 2: KWIC Index
It is usually desired to omit ``noise'' words such as ``the'' from the listing; alternatively, it may be desired to make an index that includes only ``interesting'' words from another set. Thus, a noise word dictionary or a dictionary of interesting words may be used as auxiliary data sets.
A user may want to parameterize this software framework in a number of ways:
A kwic-framework specifies a number of views and parameters; it allows considerable parameterization of the generic KWIC program, while providing defaults that allow a KWIC program to be generated from a minimal specification. There is a view from the input data type to s sequence of input items; this could be a generator that reads the input items from an external source. There is a view from an input item to its title, which must have an iterator to produce words. The title defaults to a string-of-words, for which a small parser and iterator are provided to extract individual words from a string. A parameter specifies whether to omit noise words. A noise word dictionary or noise word list may be provided; a default noise word list is built in. By default, AVL-trees are used for both the noise word dictionary and the keyword entry dictionary. A method for printing an entry may be provided.
Using this software framework, a highly parameterized KWIC program can be produced if desired. At the same time, a simple KWIC program can be generated from a very simple specification:
(simple-kwic (listof string-of-words) supers (kwic-framework))This specification can be used with a simple function to generate the specialized code (about 160 lines) from only a few lines of specification:
(gldefun t2 (b:simple-kwic) (kwic b))
(t2 '("evolution of the slithy tove"
"treasure trove of toves"
"slithy creatures of the southwest"))
produces:
slithy creatures of the sou
evolution of the sli
slithy creatures of
evolution of the slithy tove
slithy creatures of the southwest
evolution of the slithy tove
treasure trove of toves
treasure trove of to
treasure trove of toves
This section describes some of the work most closely related to the work described in this paper. Space limitations preclude a complete review of all related work. There are several useful collections of papers in this area. Krueger [krueger92] is an excellent survey of work on software reuse. The Biggerstaff and Perlis volumes [biggerstaff] contain papers on theory and applications of software reuse. [ieee:tose], [rich:readings], and [lowry91] contain papers describing Artificial Intelligence approaches to software engineering.
The Ada language was intended to foster reuse, but this goal has only partly been achieved [gautier]. Ada and related languages such as Modula-2 allow reuse of code from parameterized modules [hille] [lins]; typically, such modules implement stylized constructs such as List of type, where type can be parameterized. Our views extend this kind of parameterization by allowing composition of such a view with another view of the component type, as illustrated by the polygon example.
Functional languages such as ML [wikstrom] allow polymorphic functions to be defined; however, Standard ML does not allow functors to be applied to functors, which would be required to do the equivalent of views.
SETL [dewar] includes set datatypes and operations, with automatic selection of data representations; efficiency has not been competitive with hand-generated code [kruchten84].
Goguen [goguen86] [goguen89] proposed the use of view isomorphisms to describe connections between theories in the OBJ language. The use of views described in the present paper is more general than Goguen's because we consider views as mapping aspects of data types rather than as strict isomorphisms between types.
Gries [gries91] has proposed the use of syntactic transformations in the POLYA language. These transformations [efremidis93] are verbose and redundant; the user must verify correctness not only of transformations, but also of individual uses of them. Views are more powerful and easier to use.
The Programmer's Apprentice [rich:pabook] was based on reuse of programming clich'es, which are somewhat analogous to our generic algorithms. Programmer's Apprentice required that the user specify many rather low-level details to specialize a clich'e. In contrast, our views are higher-level specifications that are made at the level of types rather than individual sections of code.
The KIDS and DTRE systems developed at Kestrel Institute [smith90] [smith91] allow programs to be developed from formal program and data type specifications by interactive application of refinement and optimization transformations. For combinatoric search problems, KIDS allows development of correct and highly optimized programs.
The Sinapse system [kant91] synthesizes programs for simulating large systems of differential equations for seismic analysis; it produces optimized code with a high ratio of output to an input specification of roughly 50 lines.
Setliff [setliff92] has synthesized a variety of routing algorithms for VLSI design, selecting data structures and algorithms to optimize and meet constraints on speed and memory use.
Object-oriented programming (OOP) is a popular way of achieving software reuse. Views provide all the power of OOP and extend it in several important ways. Because views provide separation of name spaces and representations between an application type and abstract type, there is no need for an application type to conform to the implementation of an abstract type in order to reuse its procedures. Multiple views of an application type as different abstract types will not conflict because of the name space separation. In addition, it is possible to have multiple distinct views of an application type as the same abstract type; for example, a pipe has two useful views as a circle. Specialization and in-line compilation of generic procedures, coupled with symbolic optimization and partial evaluation, allow views to provide the conceptual benefits of a class hierarchy while producing efficient code.
We have described reuse of generic procedures by specialization through views. Views provide a clean mechanism by which an application data type can be viewed as an abstract type. Most systems of software reuse impose significant restrictions on the application, e.g., that a certain programming language be used, or that the application data meet certain requirements ( e.g., be objects that can respond to certain messages). Because views cleanly separate application data types from abstract types, it is possible to reuse generic procedures for existing application data, in an existing application language.
Views allow significant parameterization of generic procedures. Views also allow composition of generic procedures, so that one generic can be written in terms of others. A single copy of each generic procedure is sufficient for all uses.
From a user's perspective, the automated support provided for creating views makes the system fast and easy to use. The amount of code that is generated is large compared to the small amount of input specification that is required. The specifications are relatively simple and natural because they are based on programming abstractions that the user already understands. With well-designed graphical interfaces, the amount of learning required to use the system is reduced.
With reuse of generic programs through views, the programmer can be liberated from coding and can instead be a composer of mappings.
[ieee:tose] IEEE Trans. on Software Engineering, vol. 11, no. 11, Nov. 1985.
[balzer85] Balzer, R., ``A 15 Year Perspective on Automatic Programming'', IEEE Trans. on Software Engineering, vol. 11, no. 11, Nov. 1985, pp. 1257-1267.
[biggerstaff] Biggerstaff, T. and A. Perlis (eds), Software Reusability (2 vols.), ACM Press / Addison-Wesley, 1989.
[batory93] Batory, D., et al., ``Scalable Software Libraries'', Proc. ACM SIGSOFT '93: Symposium on the Foundations of Software Engineering, Los Angeles, CA, Dec. 1993.
[booch87] Booch, G., Software Components with Ada, Benjamin-Cummings, 1987.
[dewar] Dewar, R. B. K., The SETL Programming Language, manuscript, 1980.
[efremidis93] Efremidis, S. and Gries, D., ``An Algorithm for Processing Program Transformations'', Tech. Report TR 93-1389, C.S. Dept., Cornell Univ.
[gautier] Gautier, R. and P. Wallis, Software Reuse with Ada, London: Peter Peregrinus Ltd., 1990.
[goguen86] Goguen, J. A., ``Reusing and Interconnecting Software Components'', IEEE Computer, Feb. 1986, pp. 16-28.
[goguen89] Goguen, J. A., ``Principles of Parameterized Programming'', in [biggerstaff], pp. 159-225.
[gries91] Gries, D., ``The Transform: a New Language Construct'', lecture presented at the University of Texas, Feb. 18, 1991.
[hille] Hille, R. F., Data Abstraction and Program Development using Modula-2, Prentice Hall, 1989.
[kant91] Kant, E., et al., ``Scientific Programming by Automated Synthesis'', in [lowry91], pp. 169-205.
[krueger92] Krueger, Charles W., ``Software Reuse'', ACM Computing Surveys, vol. 24, no. 2 (June 1992), pp. 131-184.
[kruchten84] Kruchten, P., E. Schonberg, and J. Schwartz, ``Software Prototyping using the SETL Language'', IEEE Software, vol. 1, no. 4 (Oct. 1984), pp. 66-75.
[lamb83] Lamb, D., ``Sharing Intermediate Representations: The Interface Description Language'', Tech. Report CMU-CS-83 129, C.S. Dept., Carnegie-Mellon University, 1983.
[lins] Lins, C., The Modula-2 Software Component Library, Springer-Verlag, 1989.
[lowry91] Lowry, M. and R. McCartney, eds., Automating Software Design, AAAI Press / MIT Press, 1991.
[novak:glisp] Novak, G., ``GLISP: A LISP-Based Programming System With Data Abstraction'', AI Magazine, vol. 4, no. 3, Fall 1983, pp. 37-47.
[novak:gluser] Novak, G., ``GLISP User's Manual,'' Tech. Report STAN-CS-82-895, C.S. Dept., Stanford Univ., 1982; TR-83-25, A.I. Lab, C.S. Dept., Univ. of Texas at Austin.
[novak:tose92] Novak, G., F. Hill, M. Wan, and B. Sayrs, ``Negotiated Interfaces for Software Reuse'', IEEE Trans. on Software Engineering, vol. 18, no. 7 (July 1992).
[novak:kbse92] Novak, G., ``Software Reuse through View Type Clusters'', Proc. 7th Knowledge-Based Software Engineering Conf., McLean, VA, Sept. 1992, IEEE Computer Society Press, pp. 70-79.
[novak:views93] Novak, G., ``Creation of Views for Reuse of Software with Different Data Representations'', Tech. Report AI-TR-93-196, A.I. Lab, C.S. Dept., Univ. of Texas at Austin.
[rich:readings] Rich, C. and R. Waters (eds), Readings in Artificial Intelligence and Software Engineering, San Mateo, CA: Morgan Kaufmann, 1986.
[rich:pabook] Rich, C. and R. Waters, The Programmer's Apprentice, ACM Press, 1990.
[setliff92] Setliff, D. and R. Rutenbar, ``Knowledge Representation and Reasoning in a Software Synthesis Architecture'', IEEE Trans. on Software Engineering, 18, 6 (June 1992), pp. 523-533.
[smith90] Smith, Douglas R., ``KIDS -- A Semi-automatic Program Development System'', IEEE Trans. on Software Engineering, vol. 16, no. 9, Sept. 1990, pp. 1024-1043. [smith91] Smith, Douglas R., ``KIDS -- A Knowledge-based Software Development System'', in [lowry91], pp. 483-514.
[wikstrom] Wikstr"om, ke, Functional Programming Using Standard ML, Prentice-Hall, 1987.
float polygon_area_b_3 (poly)
POLYB *poly;
{
float area;
int flg;
POLYB *p, *firstpt, *lastpt;
area = 0.0;
flg = 0;
{
POLYB *start, *ptr;
POLYB *item;
int done;
start = poly;
ptr = start;
done = 0;
while ( ptr !(done) )
{
item = ptr;
p = item;
if (flg != 0)
{
area = area + (p-> r * cos(p-> theta)
- lastpt-> r * cos(lastpt-> theta))
* (p-> r * sin(p-> theta)
+ lastpt-> r * sin(lastpt-> theta))
/ 2.0;
lastpt = p;
}
else
{
firstpt = p;
lastpt = p;
flg = 1;
}
ptr = ptr-> next;
if (ptr == start)
done = 1;
}
}
area = area + (firstpt-> r * cos(firstpt-> theta)
- lastpt-> r * cos(lastpt-> theta))
* (firstpt-> r * sin(firstpt-> theta)
+ lastpt-> r * sin(lastpt-> theta))
/ 2.0;
return fabs(area);
}