Software Reuse by Specialization of Generic Procedures through Views

Gordon S. Novak Jr.
Department of Computer Sciences
University of Texas at Austin
Austin, Texas 78712




http://www.cs.utexas.edu/users/novak
novak@cs.utexas.edu


(512) 471-9569










September 20, 2001

Challenge: Make Programming Easier

The progress of computing is limited by the difficulty, delay, and expense of programming. A grand challenge of computer science is to enable programming by composition of large-scale components.

• Reuse generic algorithms rather than rewriting

• Adapt generic procedures for the application

• Raise the level of programming:
  • from coding of details
  • to module integration

• Reduce the detail that must be specified explicitly

Technical Challenges

• Software must be customized for the application

• Correct and efficient code must be produced

• Must reduce human cost:
  • Reduce input

  • Reduce learning

• Combine components (procedures and data) that are not designed to fit together a priori.

Our Approach

• Specialization of generic procedures

• Views describe how concrete types correspond to abstract types

• User interfaces make it easy to create views
  • VIEWAS: data structure views

  • MKV: mathematical views

• Language translation: one system and one set of generics delivers code in Lisp, C, C++, Java, Pascal.

• Automatic Programming Server synthesizes code for user over Web

• VIP: construction of scientific programs from diagrams

• Program Frameworks: collections of data structures and procedures

• Future work: Automated assistance to instantiate frameworks
  • Constraint propagation

  • Expert systems

GLISP Language and Compiler

• GLISP (Generic Lisp) is a typed Lisp

• Goal: code independent of data representation
  • Single form of access to properties:
    (property object)
    whether property is stored or computed.

  • Can store back through a computed property by algebraic inversion: ( x * 2 := y )
    or by a procedure.

• Methods and inheritance as in OOP

• In-line expansion or specialization of methods

• Expansion is recursive at compile time:
  • An operation expands to sub-operations on the implementation

  • Large code expansion is possible

  • Types inferred and propagated during expansion

• Partial evaluation and pattern-based optimization:
  • eliminates message sending at runtime
  • optimizes code
• Loops use iterator macros

Views

• A view makes a concrete type appear as an abstract type; it encapsulates a concrete type and adapts it for use with a generic procedure.

• A view has:
  • concrete type as its stored form

  • abstract type as a superclass

  • methods that translate from the concrete type to basis variables of the abstract type

  • cf. Wrapper or Adapter class in OOP [Gamma]

• Application objects may have many views.
  For example, an airplane is:
  • a machine

  • a financial asset

  • a location in space

A Simple View

(gldefun t1 (pz:pizza)
  (area (circle pz)))

(LAMBDA (PZ) (* 0.78539816 (EXPT (CADR PZ) 2)))

Computation as Simulation

A useful view is to think of all computation as
simulation. cf.: Isomorphism of semigroups ¹

Given two semigroups $G_{1} = [S, \circ]$ and
$G_{2} = [T, \ast]$, an invertible function
$\varphi : S \rightarrow T$ is said to be an isomorphism between G₁ and G₂ if, for every aand b in S,

$\varphi (a \circ b) = \varphi (a) \ast \varphi (b)$

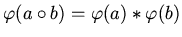
from which: $a \circ b = \varphi ^{-1} ( \varphi (a) \ast \varphi (b) )$

Views as Isomorphisms

Requirements of Views

• An abstract type is defined as an abstract record containing a set of basis variables.

• Generic procedures are written in terms of the basis variables.

• A view type emulates the abstract record using the concrete record as storage:
  • storage property: after a value is stored into a basis variable, a read of the basis variable returns the same value.

  • independence property: storing into one basis variable does not change the values of others.

• A store into a basis variable may require updating several concrete fields.

• Slight inaccuracy in emulation may be allowed (e.g., floating point round-off error in representing (x, y) using $(r, \theta)$).

Making Views

• Views may be complex: an example line-segment view is 67 lines of code.

• Views may be error-prone if written by hand: storage and independence properties must be maintained.

• Difficulty of coding view types detracts from benefit of reuse.

• Automated assistance for making views is needed.

Data Structure Views: VIEWAS

The VIEWAS system makes a view of a concrete type as a data structure type, such as a linked-list or avl-tree.

• VIEWAS makes correspondences between abstract and concrete records
  • Pointers

  • Values, e.g. field to sort on

  • Choices, e.g. sort-direction

  • Groups of fields, e.g. contents is everything except the link pointer.

• Type filtering and propagation of choices reduce input from user; simple views can be made automatically.

Example: Sorted Linked List

(part (name string)
      (size integer)
      (next (^ part)))

• The link pointer is inferred to be the next field: the only possibility allowed by type filtering.

• The sort-value is selected as name by the user.

• The sort-direction is selected as ascending.

The user only needs to make two choices from menus; then any procedure defined for sorted-linked-list can be specialized for the user's data.

Standard data structure templates can easily be instantiated with a given contents.

Views by Graphical Correspondences

Views can be specified by graphical correspondences between user data and a diagram of an abstract object.

Example: View a Christmas tree as a cone.

>(mkv 'cone 'xmas-tree)

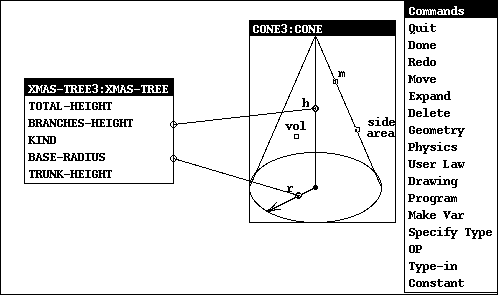
(gldefun tg (x:xmas-tree) (side-area (cone x)))

(LAMBDA (X)
  (* 3.1415926535897931
     (* (FIFTH X)
        (SQRT (+ (EXPT (FIFTH X) 2)
                 (EXPT (CADDR X) 2))))))

Mathematical Views: MKV

• User makes correspondences between a diagram of the abstract type and a menu of fields and computed properties of the concrete type.

• Buttons on the diagram correspond to variables of the abstract type

• Equations associated with abstract type are solved by symbolic algebra

• A button is removed from diagram when solved; this prevents inconsistent specification.

• Symbolic algebra is used to make a view that maintains storage and independence properties.

• An instance of concrete type can be created from a set of basis variables.

• Data translation is possible through views as a common abstract type:

Line Segment

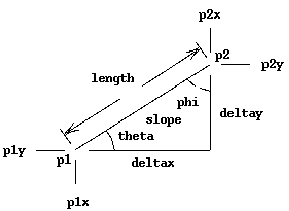
A line segment could be represented in many ways:

• two end points
• one end point, length, theta
• one end point, slope, delta-x

The figure presents variable buttons to allow nearly any representation to be specified easily.

Example of Line Segment View

(mkv 'line-segment 'ls1)

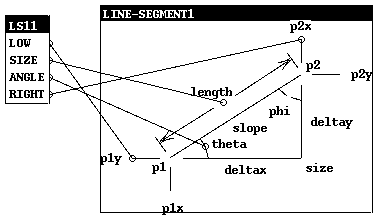
(gldefun tb (l:ls1 p:consv)
  (leftof-distance (line-segment l) p))

result type: REAL
(LAMBDA (L P)
  (- (* (COS (CADDDR L))
        (- (CDR P) (CADR L)))
     (* (SIN (CADDDR L))
        (- (CAR P)
           (- (FIFTH L)
              (* (CADDR L) (COS (CADDDR L))))))))

Line Segment Data Conversion

(mkv 'line-segment 'ls2)

(gleqns-transfer-by-view 'ls2 'ls1)

(LAMBDA (VAR-LS1)
  (LET ((VAR-LS1-VIEW VAR-LS1))
    (LIST 'LS2
          (- (FIFTH VAR-LS1-VIEW)
             (* (CADDR VAR-LS1-VIEW)
                (COS (CADDDR VAR-LS1-VIEW))))
          (FIFTH VAR-LS1-VIEW)
          (- 1.570796 (CADDDR VAR-LS1-VIEW))
          (+ (CADR VAR-LS1-VIEW)
             (* (CADDR VAR-LS1-VIEW)
                (SIN (CADDDR VAR-LS1-VIEW)))))))

Advantages of Graphical Correspondences

• Diagrams are self-documenting.

• Diagrams represent concepts that the user already knows.

• The interface is fast and easy to use.

• Reusing procedures through views is less error-prone than doing algebra by hand.

• Application data does not have to conform to a library program. The library program is converted automatically.

• User data could be used with a remote program over a network if the user and author of the program each make a view of their data as a common abstract type:

  
  
  

  This allows compatibility without conformity.

Programming by Graphical Correspondences

Related techniques make it possible to write scientific programs and solve physics problems.

• The initial diagram consists of boxes that represent input data and an output box.

• Physical laws and geometric models may be selected by menu and added to the picture.

• Connections may be made between diagram buttons and data.

• A program is generated from the diagram by symbolic data flow:
  • Initially, input data and constants are defined.

  • When a data item becomes defined, its value is propagated into boxes to which it is connected.

  • When a value is propagated into a box, equations associated with the box are examined to see whether they can be solved for other variables.

  • Code is generated as a side-effect of the data flow.

• Units of measurement are converted automatically.

Calculation of the Mass of the Sun

result type: (UNITS REAL KILOGRAM)

(LAMBDA () 1.9660057055546021E30)

Aircraft Position from Radar Data

(vip
  '((TIME-DIFF         (UNITS INTEGER (* 100 NANOSECOND)))
    (AIRCRAFT-ALTITUDE (UNITS INTEGER (* 10 FOOT)))
    (RADAR-ALTITUDE    (UNITS INTEGER (* 10 FOOT)))
    (RADAR-ANGLE       (UNITS INTEGER (/ (* 2 PI RADIANS)
                                         4096)))
    (RADAR-UTM         UTM-VECTOR))

Aircraft Position Program

(LAMBDA (TIME-DIFF: (UNITS INTEGER (* 100 NANOSECOND))
         AIRCRAFT-ALTITUDE: (UNITS INTEGER (* 10 FOOT))
         RADAR-ALTITUDE: (UNITS INTEGER (* 10 FOOT))
         RADAR-ANGLE: (UNITS INTEGER (/ (* 2 PI RADIANS)
                                        4096))
         RADAR-UTM:UTM-CVECTOR)
  (LET (OUT7 OUTPUT D3 OUT8 X5 Y3 X6 RELPOS:UTM-CVECTOR)
    (OUT7 := (- AIRCRAFT-ALTITUDE RADAR-ALTITUDE))
    (D3 := (* '(Q 2.997925E8 (/ M S)) TIME-DIFF))
    (OUT8 := (/ D3 2))
    (X5 := (SQRT (- (EXPT OUT8 2) (EXPT OUT7 2))))
    (Y3 := (* X5 (SIN RADAR-ANGLE)))
    (X6 := (* X5 (COS RADAR-ANGLE)))
    (RELPOS := (A UTM-CVECTOR NORTH Y3 EAST X6))
    (OUTPUT := (+ RELPOS RADAR-UTM))
    OUTPUT))

Aircraft Position Program in C

CUTM  *tqc (time_diff, aircraft_altitude, radar_altitude,
            radar_angle, radar_utm)
  long time_diff, aircraft_altitude, radar_altitude,
       radar_angle;
  CUTM  *radar_utm;
  {
    long out7;
    CUTM  *output;
    float d3, out8, x5, y3, x6;
    CUTM  *relpos,  *glvar4796;
    out7 = aircraft_altitude - radar_altitude;
    d3 = 2.997925E8 * time_diff;
    out8 = d3 / 2;
    x5 = sqrt(square(out8) - 9.2903039999999988E14
                             * lsquare(out7));
    y3 = x5 * sin(0.0015339807878856412 * radar_angle);
    x6 = x5 * cos(0.0015339807878856412 * radar_angle);
    relpos = (CUTM*) malloc(sizeof(CUTM));
    relpos->north = 1.0000000000000001E-7 * y3;
    relpos->east = 1.0000000000000001E-7 * x6;
    glvar4796 = (CUTM*) malloc(sizeof(CUTM));
    glvar4796->east = relpos->east + radar_utm->east;
    glvar4796->north = relpos->north + radar_utm->north;
    output = glvar4796;
    return output;
  }

Language Translation

Specialized procedures can be delivered in several languages: Lisp, C, C++, Java, Pascal.

• Lisp is equivalent to abstract syntax trees used by compilers

• Data structures in other languages can be specified to GLISP

• Simulated data structures in Lisp can be used for rapid prototyping

• Program transformation:
  • Transform Lisp features, e.g. returning a value from if statement

  • Patterns transform Lisp idioms to target idioms

• Syntactic transformation: names, types, patterns

• Printing program produces formatted, readable code.

Automatic Programming Server

The Automatic Programming Server operates over the Web and writes specialized procedures for the user.

• User describes concrete data types

• User makes views showing how concrete types correspond to abstract types known to the system

• User selects desired procedures

• Procedures are specialized, translated to target language, and delivered as a source code file.

• Data conversion programs can also be generated.

• Example: avl-tree: 200 lines of generated code in less than a minute of user time.

Automatic Programming Server

• User defines a part data structure:

  (part (name string)
        (size integer)
        (next (^ part)))
  

• User makes a view as a sorted linked list

• User chooses desired procedures

Program Framework

A program framework is a large-scale generic program whose components are other generics and data structures. A framework can be instantiated by plugging in appropriate procedural and data components.

Example: Key Word in Context (KWIC) index program. This framework has parameters:

• Input data record. This will contain a title, and may contain other information that will be printed.

• Noise word dictionaries. There may be a general noise word dictionary and a domain-specific one.

• Data structures for storing instances of key words. These will be specializations of abstract data structures, e.g. an avl-tree of symbols with a linked list of occurrences.

• Method for printing the output.

Programming by Combining Components

Hypothesis: Although there is much detail in a program, there are many fewer significant decisions to be made. Most details can be derived from these decisions or defaulted.

• The title record will contain a subset of the fields of the input record.

• Only the fields that will eventually be printed need to be stored.

• A standard dictionary of noise words will usually be adequate.

• The entry storage can be defaulted to an avl-tree containing word entries.

• A word entry will contain a string and a pointer to a linked list of occurrences.

• Each occurrence will have a pointer to a title record and a column number.

Constraints from various parts of the program can be propagated to specialize the data structures needed. Given the data structures and views, the program components can be specialized.

Future Work

Graphical program specifications as used in VIP could be adapted for specification of larger programs using frameworks.

• A framework gives a large-scale structure with program and data components to be filled in.

• Connection of two components may constrain both.

• Constraint propagation through the network can maintain consistency and avoid redundant specification.

• Constraint violations can be treated not as errors, but as subproblems to be solved, e.g. by converting data to the needed form.

• The system can make defaults using rules, or offer intelligent choices of components (both data and programs).

Constraint propagation and symbolic inference can fill in details based on major decisions by the user.

Related Work

• Browne, Werth, Newton et al.: CODE/ROPE system generates code for parallel structuring of programs.

• Batory et al.: GENESIS system allows creation of a database system from components.

• Kant et al., Scicomp: Synapse system generates code for numerical simulation of differential equations.

• Smith et al., Kestrel Institute: KIDS system generates code by correctness-preserving transformations from a formal specification.

• Waldinger and Manna: generate a program by constructive proof from a formal specification using deductive tableaux.

• Setliff: generation of wire-routing programs.

• Goguen: uses views specified as isomorphisms in OBJ.

• Gries: transforms used to transform code into application form.

• Object-oriented programming: reuse of generic procedures.

Summary

Views are powerful.

• Views enable:
  • Specialization of generic algorithms

  • Data translation

  • Graphical interfaces
• A single view provides access to all of the generic procedures associated with the view
  (28 procedures for linked-list).

• Views are easily created with smart interfaces.

• Reuse of carefully written generic algorithms can provide improved program quality and performance.

• Views allow easier modification of programs and data.

These techniques may achieve the grand challenge of making programming much easier by reuse of components.

Constraint Propagation

  

Figure 1: Simple Example Framework

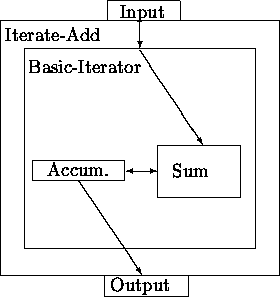The Iterate-Add framework is an abstraction of a large number of programs. Specifying the type of the input as (listof integer) allows the whole framework to be instantiated by propagation of facts via rules.

result type: INTEGER
(LAMBDA (SEQ3)
  (LET (ITEM4 ACC5)
    (SETQ ACC5 0)
    (DOLIST (ITEM4 SEQ3) (INCF ACC5 ITEM4))
    ACC5))