Negotiated Interfaces for Software Reuse

Author's present address: Fredrick N. Hill, 413 Tulane SE, Albuquerque NM 87106.

Copyright © 1992 by IEEE.

Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works must be obtained from the IEEE.

This article appears in IEEE Transactions on Software Engineering, vol. 18, no. 7 (July 1992), pp. 646-653.

This research was supported by the U.S. Army Research Office under contract DAAG29-84-K-0060. Computer equipment used in this research was donated by Xerox Corporation and Hewlett Packard.

• Postscript version of paper

Abstract

A significant barrier to the reuse of software is the rigid interface presented by a subroutine. For nontrivial data structures, it is unlikely that the existing form of the data of an application will match the requirements of a separately written subroutine. We describe two methods of interfacing existing data to a subroutine: generation of a program to convert the data to the form needed by the subroutine and rewriting the subroutine, through compilation, to fit the existing data. Both methods can be invoked through easily used menu-based negotiation with the user. These methods have been implemented using the GLISP language and compiler.

Introduction

Much of the work of programming consists of rewriting standard algorithms for use in the application of interest. Reuse of previously written subroutines that implement the desired algorithms has the potential to reduce the cost of software, increase the speed of software production, and increase reliability. However, there presently is relatively little reuse of software in practice.

A significant barrier to the reuse of software is the rigid interface presented by a subroutine. The actual arguments in a subroutine call must exactly match the formal arguments in the subroutine's definition: there must be the same number of arguments, they must be in the right order, and their data types must match. Other properties, such as the units of measurement of numeric values, must also match. Strongly typed languages enforce some of these requirements; however, all the requirements must be met whether they are enforced by the language or not: failure to do so will result in runtime errors or incorrect answers. Most reuse of software occurs where compatibility of arguments occurs naturally because the argument types are simple ( e.g., sqrt requires only a single floating-point number) or are types whose form is made compatible by the language ( e.g., arrays).

For nontrivial data structures, it is unlikely that the data types of an application will match those of a separately written subroutine. The application data may use a different record format; it may also contain extra fields, lack some fields that are present in the type used by the subroutine[The subroutine might be written using abstract data types that contain fields not used by that particular subroutine; for example, a circle object might be defined with a center data field that is not used in computing the area of the circle.], use different names for fields, or specify data in a different form[For example, an application circle could be specified using its diameter, while the subroutine might use the radius instead.] or using different units of measurement. If the application data do not match the arguments required by a subroutine, it will be necessary to convert the data into the expected form prior to the subroutine call, and possibly also to convert the subroutine's results (Figure 1), or it will be necessary to rewrite the subroutine to use the existing data.

Fig. 1: Interfacing existing data to a subroutine

In traditional programming, this conversion of data or code discourages reuse. Since conversion requires hand-written code, the benefit of reuse is reduced. A data conversion program requires time to run, space for its code, and space to make new copies of the data (a serious disadvantage for large data sets).

We describe two methods for semi-automatic interfacing of application data to an existing subroutine. In the first method, a data conversion program is generated automatically from a specification of correspondences between the application data and the data required by the subroutine; this specification is obtained through a menu-based negotiation with the user. In the second method, a connection type is produced (also using menu-based negotiation) that describes how the application data correspond to the abstract data used by a generic program. Compilation of the generic program using the connection type produces a specialized version that operates directly on the application data. Both methods make it relatively easy to reuse a subroutine for application data whose types are different from the types for which the subroutine was originally written.

Related Work

Software Reuse

Biggerstaff and Perlis [biggerstaff] contains papers on theory and applications of software reuse. The Ada language was intended to foster reuse, but this goal has only partly been achieved [gautier]. Modula-2 [hille] [lins] allows reuse of code from external modules; typically, such modules implement constructs such as List of < type> , where < type> is an application type.

Artificial Intelligence approaches to software engineering have included transformations from specifications to code and reuse of code fragments or specifications; [ieee:tose] and [rich:readings] contain papers describing these approaches. The Programmer's Apprentice [rich:pabook] was based on reuse of programming cliches; it had little use of types in the language and required the programmer to edit output code.

Functional languages such as ML [wikstrom] allow polymorphic functions to be defined; it is not clear that such languages are presently suitable for general applications use.

Data Translation

IDL ( Interface Description Language) [lamb83] was designed to allow exchange of large structured data between separately written components of a large software system, such as an Ada compiler. IDL accepts the output of one phase of the compiler, reformats it into a ``flat'' form that can be written to an external file, and allows such a file to be read into a (possibly different) data structure for the following phase. The data structures involved may be large graph structures, so IDL allows for structure sharing. Use of IDL requires precise specifications of both data formats.

Herlihy and Liskov [herlihy] describe a method for transmission of structured data over a network, with a possibly different representation at the destination. Their method requires writing procedures to encode and decode the data into transmissible representations; they also describe a method for transmission of shared structures. The programs described in the present paper do not handle data involving shared structures.

Object-oriented Programming

Object-oriented programming (OOP) has been promoted as a way of achieving software reuse, but there are problems with reuse in OOP. Not only must an object accept all the messages that will be sent to it, but the results returned must be objects that will accept all the messages that may be sent to them, and so on. Side-effects of messages may cause unexpected effects. Thus, the type requirements of an object-oriented interface may be as rigid as those of an ordinary subroutine. If reuse is accomplished by inheritance of methods from generic objects, there may be name conflicts. For example, a pipe might have an inside-radius and an outside-radius, so that it could not directly inherit methods from circle that expect a single radius property: while radius could be aliased to either inside-radius or outside-radius, it could not be aliased to both.

A second problem with OOP is inefficiency. Since most messages perform actions that are small (often only access to data), the overhead of message interpretation is large relative to the cost of the operation. When systems are layered, this overhead is repeated. The opacity of objects prevents optimization: if multiple operations are done by messages to objects, it will not be possible to optimize the operations by combining them. Materialization of objects that are used only temporarily has a high cost. These efficiency problems inhibit reuse.

The techniques we describe provide the conceptual benefits of OOP while avoiding many of these problems.

GLISP Language and Compiler

GLISP [novak:glisp,novak:aaai83,novak:sigplan83,novak:gluser] is a high-level language with abstract data types that is compiled into Lisp. It allows the data structure of an object to be specified, so that the programmer has control of the structure and representation of data. Many features of GLISP are easily understood as extensions to object-oriented programming; a GLISP type is analogous to a class in OOP. Associated with each type are message-like operations; computed properties are side-effect-free operations involving only the object itself. The syntax of references to computed properties and stored data is the same, so that the form of program code does not depend on whether a given piece of data is stored or computed. As in OOP, there is a hierarchy of types; messages can be inherited from parent types. Since generic objects and operations on them can be described, generic programs can be written in terms of objects and operations on objects rather than in terms of the implementations of objects.

GLISP supports run-time message sending; however, it is desirable to compile in-line code rather than interpreted message calls. The GLISP compiler keeps track of the types of objects at compile time and uses type inference to infer the types of derived objects. When the type of an object is known at compile time, a message to the object can be compiled as a direct function call, or a specialized version of a generic function can be compiled, or the function can be expanded and compiled in-line. Specialization and in-line expansion are recursive at compile time and are based on actual compile-time types. This allows a simple source code operation to undergo multiple levels of expansion, with parts of the expansion being drawn from the types of the objects involved as expansion proceeds. Symbolic optimization folds operations on constants, removes unnecessary code, and combines operations where appropriate; this improves efficiency and provides conditional compilation by eliminating conditionals when the test is evaluable at compile time. Code inversion  automatically inverts algebraic expressions and extraction of data from structures, allowing values to be stored back ``through messages'' when needed. These features are illustrated in the following sections.

Data Structures

Data representation is a barrier to reuse in most languages, since the form of program code differs for different data structures and for data that is computed rather than stored; this prevents reuse of code for alternative implementations of data.

GLISP has a data description language that allows the desired data representation to be specified; this language is sufficient for describing most Lisp data structures and can be extended to describe data structures in other languages.

The following examples show how the same code can be used with data that are represented in different ways. Two variants of circle are defined: the first stores the radius, while the second stores diameter using a different record structure.

(circle  (list (center vector) (radius real))     ; the data structure
  prop   ( (area (pi * radius ^ 2)) ) )           ; a computed property

(dcircle (cons (diameter real) (color symbol))    ; different data
  prop   ( (radius (diameter / 2)) )              ; radius is computed
  supers (circle))                                ; inherits from circle

[The syntax of function definitions is (gldefun function-name (arguments) code) ; gldefun stands for ``GLisp DEfine FUNction''. In actual code, the character : is written with a back-slash escape character for compatibility with Common Lisp; our examples omit the back-slash for readability.]

[ (EXPT x 2) is the way of writing x ². CADR and CAR are references to the radius and diameter parts of the data structures.]

(gldefun t1 (c:circle)  (area c))    (LAMBDA (C)
                                       (* PI (EXPT (CADR C) 2)))

(gldefun t2 (c:dcircle) (area c))    (LAMBDA (C)
                                       (* 0.7853982 (EXPT (CAR C) 2)))

In order to reuse code, it must be possible not only to ``read'' data that is computed rather than stored, but also to ``store into'' computed data; this is done by automatic algebraic inversion: [Properties that are algebraic functions of a single stored value can be inverted automatically. An attempt to store into a property that cannot be inverted will result in an error message.]

(gldefun t3 (c:dcircle v:real)       (LAMBDA (C V)
  ((area c) := v)                      (RPLACA C (* 1.128379 (SQRT V)))
  c)                                   C)

These examples illustrate features of the GLISP language and compiler that are used to implement the reuse capabilities described below.

Reformatting Data

A typical way to interface existing data to a subroutine is to write a conversion program to reformat the data. Unfortunately, this normally requires that a programmer understand both the form of the existing data and the form required by the subroutine, then write code to reformat the data.

Man-Lee Wan has written a program, LINK [wan], that automatically writes an interface conversion program. It is assumed that both the existing data and the data required by the subroutine have been described as GLISP types. From these two descriptions, LINK conducts a menu-based negotiation to determine how the data required by the subroutine can be derived from the existing data. For example, a subroutine that draws a pie chart might require as input a list of pairs, where each pair consists of a title for a slice of the pie and a numeric value representing the size of the slice:

   (listof (list (title symbol)
                 (value number)))

   ((COOKIES 27200) (CANDY 84400) (VEGETABLES 2720))

The task of the LINK program is to match the specifications of the required data and the available application data, then create a program (in GLISP) to derive the data values, make the data structures, and call the subroutine.

Derivation of the correspondence between the specification and the available data is done recursively. When the specification requires a set of items (in this case, a listof items), semantic filtering is applied to the description of the available data to determine which stored or computed features of the available data can produce a set of items; a menu of such features is presented to the user for selection. The user can optionally specify a predicate to determine which members of the input set are to be included; this can be a predefined predicate associated with the member objects, or it can be specified as an expression through operator and operand menus.

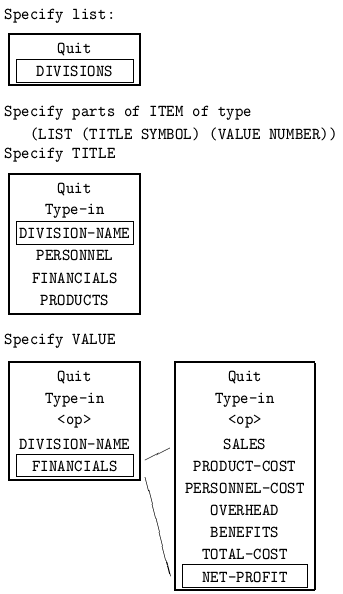
Fig. 2: Interface Specification by Menu Selection

An example of this process is shown in Figure 2. In response to the listof specification, a menu is presented to select the set of items from which to construct the input; the user selects DIVISIONS. Next, the components of the listof item must be derived from the corresponding item of the selected set; in our example, the title and value must be derived from a DIVISION. The user selects DIVISION-NAME as the TITLE. When the application data type has multiple levels of structure, successive menus are presented to descend through the types. In this example, the desired data is reached by first selecting FINANCIALS from the data for a DIVISION, then NET-PROFIT within the FINANCIALS. Arithmetic expressions can also be specified by menu, using the data available from the type as operands.

This sequence of menu selections results in the following GLISP program:

(LAMBDA (COMPANY3:COMPANY)
  (FOR DIVISION1 IN (DIVISIONS COMPANY3)
       COLLECT (A (LIST (TITLE SYMBOL)
                        (VALUE NUMBER)) WITH
                  TITLE (DIVISION-NAME DIVISION1)
                  VALUE (NET-PROFIT (FINANCIALS DIVISION1)))))

(LAMBDA (COMPANY3)
  (MAPCAR #'(LAMBDA (DIVISION1)
              (LIST (CAR DIVISION1)
                    (LET ((SELF (CADDR DIVISION1)))
                      (- (CAR SELF)
                         (+ (+ (+ (CADR SELF) (CADDR SELF))
                               (* 0.28 (CADDR SELF)))
                            (CADDDR SELF))))))
          (CADR COMPANY3)))

We can describe the process of data translation more formally as follows. Given a source type S and a goal type G , we wish to produce a function f: S --> G . In most cases, the function f will simply transfer data fields or predefined properties of S into corresponding data fields of G . Acquisition of the transfer function f can be done by recursion on the source type S , source code s , and goal type G using the following cases on the type G :

1. G is a basic type ( integer, symbol, etc.):
   Obtain the function f: S --> G by presenting a menu consisting of Type-in, < op > , If, and the names of data and computed properties of type S . If the user selects:
   1. Type-in: f = constant data of type G , entered by the user.

   2. < op > : Make an expression f = op(f₁(s), f₂(s)) of type G whose operator op is selected from an operator menu and whose operand(s) are recursively acquired as f₁: S --> G and f₂: S --> G .

   3. If: Acquire f_c: S --> boolean, f₁: S --> G , and f₂: S --> G . Return the expression f = (if f_c(s) then f₁(s) else f₂(s) ).

   4. a name: Let T be the type of the data or computed expression name.
      1. If G = T , return f = (name s) .

      2. Otherwise, let f₁ = (name s) ; this provides a function f₁: S --> T . Recursively acquire a function f₂: T --> G and return f = f₂ f₁ .

2. G is a record type, r ((n₁ G₁) ... (n_k G_k)) ,
   where r is the record type and its components are named n₁ , with type G₁ , through n_k , with type G_k . Collect functions f₁ through f_k , where f_i: S --> G_i . Return code to create record r from f₁(s) , ... , f_k(s) , f = (a r with n₁ = f₁(s) ... n_k = f_k(s) ) .

3. G is a sequence, e.g. (listof G_e), where G_e is a type.
   Obtain a function f_s: S --> sequence(T) , a function f_e: T --> G_e that maps the element type T of the sequence to the goal element type G_e , and optionally a predicate p_e: T --> boolean that selects the elements of the sequence to be included. Return the code f = (for i in f_s(s) when p_e(i) collect f_e(i) ).

4. G is a named, non-basic type:
   1. If there is stored data or a computed function of type G that is defined for type S , the user may select it as described in case 1 above.

   2. If there is a known function f: S --> G for translating from S to G , including the function presently being developed, it can be selected. [Allowing recursive use of the function that is being developed permits translation of recursive data types such as trees.]

   3. If the user selects the option Parts, acquire the function f: S --> rep(G) , where rep(G) is the data representation of type G , as described in case 2 above.

5. G is a pointer to type T_G :
   Select data within S to yield f₁: S --> ( T_S) . Acquire a function f₂: T_S --> T_G (often the function presently being developed). Return the code
   f = (if (not (null f₁(s) )) then f₂(f₁(s)) ).

The result is an interface program (in GLISP) that accepts the given data set and produces a new data set in the proper format, then calls the subroutine with the converted data. Figure 3 shows this process schematically. From the user's perspective, the existing subroutine has been converted into a version that works directly with the user's data in its original form (dotted box).

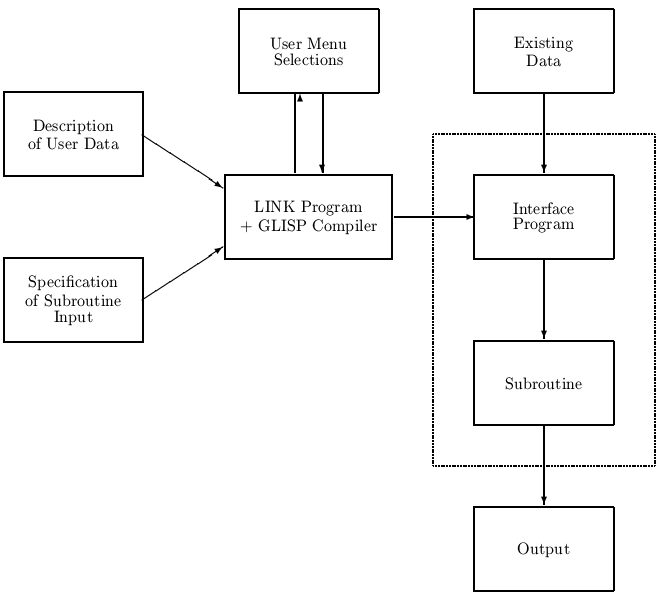
Fig. 3: Interfacing existing data to a subroutine using LINK

Use of such a program to produce interfaces has several advantages:

1. Creation of an interface program is fast.

2. It is possible to convert data between different record formats, to perform computations on data items, to convert between different types of sequences ( e.g., to convert from an array to a list), and to convert recursive structures such as lists or trees.

3. The user does not have to understand the details of either the existing data or the interface to the subroutine. The user must be able to find an appropriate subroutine for the desired use and be able to match names appearing in the interface specification to names of corresponding data. However, the user does not need to know the actual data structures involved, nor whether particular data are stored or computed.

   It would be relatively easy to provide data descriptions for databases or other data sets and to associate descriptions of data requirements with library programs. Given such descriptions, we believe that for simple programs and familiar data sets, a non-programmer could create the interface and use the program without assistance.

4. Type checking is performed by presenting only correct types as choices or by continuing the negotiation process until a correct type is reached.

5. Reusing programs by copying and modifying the data is an efficient method when the data sets are relatively small.

6. This technique could be used to allow data from one location in a network to be used with a program at another location, or to combine data sets in different formats.

Margaret Reed-Lade has written a program [reed-lade] that can semi-automatically construct a grammar and parse tabular data or data in the form of running text. Such data might exist as a text file or be input using an optical scanner. This program also produces a GLISP description for the data, allowing the data to be fed into application programs using the LINK program. The combination of these programs provides connectivity from printed data to an application using that data.

Compilation of Generic Programs

The GLISP compiler can specialize a generic program, written in terms of abstract data types, so that it operates directly on application data whose types are instances of the abstract types. This is accomplished in the following way. The generic program is compiled, with the actual types of the arguments replacing the types that appear in the definition of the program. References to data or computed properties of these arguments give results whose types are derived through type inference, and these types are propagated during compilation. Operations or messages to objects may be type-dependent, so that the same generic code can expand into quite different output code when used for objects of different types.

As an example, consider a generic function for addition of two-element (x y) vectors:

   (gldefun vectorplus (u:vector v:vector)
     (a (typeof u) with x = (x u) + (x v)
                        y = (y u) + (y v) ) )

   (vector (list (x integer) (y integer))
     msg  ((+ vectorplus open t)))

   (svector (cons (y string) (x string))
     supers (vector))

   (vofv  (list (x vector) (y vector))
     supers (vector))

(gldefun t4 (u:vector v:vector) (u + v))
(LAMBDA (U V)
        (LIST (+ (CAR U) (CAR V))
              (+ (CADR U) (CADR V))))

(gldefun t5 (u:svector v:svector) (u + v))
(LAMBDA (U V)
        (CONS (CONCATENATE 'STRING (CAR U) (CAR V))
              (CONCATENATE 'STRING (CDR U) (CDR V))))

(gldefun t6 (u:vofv v:vofv) (u + v))
(LAMBDA (U V)
        (LIST
          (LET ((G63 (CAR U)) (G64 (CAR V)))
            (LIST (+ (CAR G63)  (CAR G64))
                  (+ (CADR G63) (CADR G64))))
          (LET ((G65 (CADR U)) (G66 (CADR V)))
            (LIST (+ (CAR G65)  (CAR G66))
                  (+ (CADR G65) (CADR G66))))))

Connection Types

The above examples illustrate the compilation of generic programs for data that are instances of an abstract type, i.e., that have the abstract type as a superclass and that have all of the data elements needed by the superclass as stored data or computed properties, with the same names used in the superclass. In general, these requirements will not be satisfied by application data:

1. Application data may use different names for data than are used in the abstract type.

2. Application data may have components that are equivalent, but not identical, to those used in the abstract type, e.g. use of diameter rather than radius to specify the size of a circle.

3. There may be multiple ways of viewing application data as being of a given abstract type. For example, a pipe could be viewed as a circle using either its inside-radius or outside-radius; both views might be useful, so it would not be adequate simply to alias the name radius to one of them.

4. Application data may have names that conflict with names in the abstract type.

Fig. 4: Connection type to view a planet's orbit as a circle

A connection type can be used to view application data as an instance of an abstract type. A connection type has the application data as its stored form, the abstract type as a superclass, and computed properties that express the data needed for the abstract type in terms of the data or properties available in the application data. Figure 4 illustrates how the orbit of a planet can be viewed as a circle through the connection type planet-orbit-as-circle. planet-orbit-as-circle has as its stored data a single item p of type planet, a computed property radius that is computed as the orbit-radius of p, and the superclass circle. Given these definitions, properties of the circle abstract type, such as its area, are available through the view:

   (gldefun t7 (pc:planet-orbit-as-circle) (area pc))

   (LAMBDA (PC)
     (* PI (EXPT (GET PC 'ORBIT-RADIUS) 2)))

Negotiated Interfaces for Connection Types

When the data structures involved are more complex, it becomes difficult to make correct connection types. Careful attention must be paid to type declarations in a connection type so that type inference will produce types at the proper level of description. For example, in a tree structure the children property of the connection type must produce a set of items whose type is the connection type (not the application type). Because of the difficulty of making correct connection types, automated assistance is needed. Fredrick Hill has written a program [hill] called NI that allows a connection type to be constructed automatically from correspondences between application data and specifications of the abstract data required by a generic program; these correspondences are acquired through a menu-based negotiation process similar to that described earlier. Following the negotiation process, the generic program is compiled using the connection type, which results in a version of the program that is specialized for the application data.

An example used with Hill's program is a generic program for drawing a diagram of a tree structure. Such a program would seldom be found in a program library because of the wide variety of possible tree structures that might be used. [Some Lisp systems feature tree-drawing packages, but they require data conversion to a specified form.]

In the negotiation process for the tree-drawing program, the user specifies:

1. the application data type that is the node of the tree

2. how to tell whether a node is terminal

3. how to get the children of a node

4. what printed representation is desired for a node.

The result of compiling the generic tree-drawing program using the connection type is a specialized program to draw the user's tree in the desired fashion. A given tree can be drawn in various ways; Figure 5 shows a family tree drawn to show only the females (empty boxes represent unmarried males). Figure 6 shows an n-bit integer drawn as a tree; successors are obtained by dividing the bits in the binary representation of the integer into left and right halves until a single bit or a value of zero is reached. These examples illustrate how the same generic algorithm can be automatically recompiled to operate on quite different data. The technique of recompiling a program using a connection type is powerful: several pages of specialized code can be produced in a few seconds. In the case of Figure 6, it took longer to check the tree by hand than it took to produce the program.

Fig. 5: A Family Tree Showing Only Females

Fig. 6: An Integer Viewed as a Tree

Specialization using connection types is more powerful than copying and translation of data because it can be used with algorithms that modify the structure of data, e.g. a program to insert a new record at the end of a queue by modifying pointers. Specialization allows the insertion to be done efficiently by direct manipulation of the pointers in the original data structures. The ability of GLISP programs to ``store through'' a message by code inversion is essential to this capability.

Conclusions

We have described two methods for achieving reuse of programs by interfacing application data to separately written subroutines. These methods improve existing practice because they allow interfaces to be created quickly and require only partial understanding of data types and subroutine specifications by the user. The compiled code is efficient. These methods allow reuse of programs for application objects that are not direct instances of generic objects, but can be viewed as such instances.

The techniques described here can be used with an object-oriented system by creating ``wrapper'' objects, analogous to our connection types. A wrapper object has another object as its data; it translates messages associated with a view into corresponding messages to the original object and has the view class as a superclass. Creating wrapper objects can be inefficient and difficult, especially for pointer structures. If the object-oriented system allows a message to an object to be interpreted relative to a specified alternative class, the effect of wrapper objects can be achieved without actually creating them.

We believe that it would be possible to use the techniques described here, with the GLISP compiler, to create programs in languages other than Lisp. This could be done by defining the data types and operations of the target language as GLISP types and post-processing the Lisp output into the syntax of the target language (flagging as errors any Lisp operations that remained). However, this capability remains to be demonstrated.

The systems described here are useful, but additional work remains to be done. The LINK program performs conversion between application data and subroutine, but does not convert the output of the subroutine. In simple cases, a similar conversion of the output data would suffice; however, it would be better to produce the desired output directly. LINK can translate data that are recursive, but not data that share structure.

The NI program considers only a single main data type and a program that deals with that type. In general, it is necessary to deal with multiple types that are related. For example, a symbol table involves the record that stores information about a symbol, as well as index tables used to provide fast lookup of a symbol. Making connection types for such structures requires mechanisms for representing clusters of related types and referring to related types within a cluster for type inference; these will be described in a forthcoming paper.

Acknowledgement

We thank the referees for helpful suggestions for improving this paper.

Biggerstaff 99

[ieee:tose] IEEE Transactions on Software Engineering, vol. SE-11, no. 11, Nov. 1985.

[biggerstaff] Biggerstaff, Ted J. and Perlis, Alan J., eds., Software Reusability (2 vols.), ACM Press / Addison-Wesley, 1989.

[gautier] Gautier, R. J. and Wallis, P. J. L., Software Reuse with Ada, London: Peter Peregrinus Ltd., 1990.

[herlihy] Herlihy, M. and Liskov, B., ``A Value Transmission Method for Abstract Data Types'', ACM Trans. on Programming Languages and Systems, vol. 4, no. 4 (Oct. 1982), pp. 527-551.

[hill] Hill, Fredrick N., ``Negotiated Interfaces for Software Reusability'' (thesis), Tech. Report AI-85-16, A.I. Lab, C.S. Dept., Univ. of Texas at Austin, 1985.

[hille] Hille, R. F., Data Abstraction and Program Development using Modula-2, Prentice Hall, 1989.

[lamb83] Lamb, David A., ``Sharing Intermediate Representations: The Interface Description Language'', Tech. Report CMU-CS-83 129, Computer Science Dept., Carnegie-Mellon University, 1983.

[lins] Lins, Charles, The Modula-2 Software Component Library, Springer-Verlag, 1989.

[novak:glisp] Novak, G., ``GLISP: A LISP-Based Programming System With Data Abstraction'', AI Magazine, vol. 4, no. 3, Fall 1983, pp. 37-47.

[novak:aaai83] Novak, G., ``Knowledge Based Programming Using Abstract Data Types,'' Proc. National Conference on Artificial Intelligence (AAAI-83), Washington, D.C., August, 1983.

[novak:sigplan83] Novak, G., ``Data Abstraction in GLISP,'' Proc. SIGPLAN '83 Symposium on Programming Language Issues in Software Systems; ACM SIGPLAN Notices, vol. 18, no. 3 (June 1983).

[novak:gluser] Novak, G., ``GLISP User's Manual,'' Tech. Report STAN-CS-82-895, C.S. Dept., Stanford Univ., 1982, 91 pp.

[reed-lade] Reed-Lade, Margaret G., ``Grammar Acquisition and Parsing of Semi-Structured Text'' (thesis), Tech. Report AI-89-105, Artificial Intelligence Laboratory, Univ. of Texas at Austin, 1989.

[rich:readings] Rich, C. and Waters, R., eds., Readings in Artificial Intelligence and Software Engineering, Morgan Kaufmann Publishers, San Mateo, CA, 1986.

[rich:pabook] Rich, C. and Waters, R., The Programmer's Apprentice, ACM Press, 1990.

[schaefer] Schaefer, Marvin, A Mathematical Theory of Global Program Optimization, Prentice-Hall, 1973.

[wan] Wan, Man-Lee, ``Menu-Based Creation of Procedures for Display Of Data'' (thesis), Tech. Report AI-85-18, A.I. Lab, C.S. Dept., Univ. of Texas at Austin, 1985.

[wikstrom] Wikstr"om, ke, Functional Programming Using Standard ML, Prentice-Hall, 1987.