CS 377P Assignment 4

Due: March 28th, 2019

You can work in groups. Each group should not have more than 2 students. Each group should do the assignment independently.

Cache-optimized MMM:

In class, we described the structure of the optimized MMM code produced by ATLAS. The "computational heart" of this code is the mini-kernel that multiplies an NBxNB block of matrix A with an NBxNB block of matrix B into an NBxNB block of matrix C, where NB is chosen so that the working set of this computation fits in the L1 cache. The mini-kernel itself is performed by repeatedly calling a micro-kernel that multiplies an MUx1 column vector of matrix A with a 1xNU row vector of matrix B into an MUxNU block of matrix C. The values of MU and NU are chosen so that the micro-kernel can be performed out of the registers. Pseudocode for the mini-kernel is shown below (note that this code assumes that NB is a multiple of MU and NU).

//mini-kernel
for(int j = 0; j < NB; j += NU)
 for (int i = 0; i < NB; i += MU)
 load C[i..i+MU-1, j..j+NU-1] into registers
 for (int k = 0; k < NB; k++)
 //micro-kernel
 load A[i..i+MU-1,k] into registers
 load B[k,j..j+NU-1] into registers
 multiply A's and B's and add to C's
 store C[i..i+MU-1, j..j+NU-1]

(a) (10 points) Write a function that takes three NxN matrices as input and uses the straight-forward ikj 3-nested loop version of MMM to perform matrix multiplication. Use the allocation routine given in the implementation notes to allocate storage for the three arrays. Run this code to multiply matrices of various sizes (we recommend not going above 200x200), and draw a graph of GFlops vs. matrix size. Using PAPI counters, measure the L1 data-cache misses for the largest matrix size. What fraction of peak performance do you get for large matrices? Explain your results briefly.

(b) (20 points) To measure the impact of register-blocking without cache-blocking, implement register-blocking by writing a function for performing MMM, using the mini-kernel code with NB = N (you should verify that this implements MMM correctly). You can use the results in the Yotov et al study of the ATLAS system to determine good values for MU and NU, or you can experiment with different values to find good values. In this part, do not use vector operations in your code. Run the code to multiply matrices of various sizes, and draw a graph of GFlops vs. matrix size (the graph can be superimposed on the graph from part (a)). Using PAPI counters, measure the L1 data-cache misses for the largest matrix size. Explain your results briefly. Note for experiments: use values of N that are multiples of your values for MU and NU; otherwise, you will have to write some clean-up code to handle leftover pieces of the matrices.

(c) (20 points) Repeat part (b) but this time, use vector intrinsics to implement the MMM code. Measure the GFlops you obtain for a range of matrix sizes, and plot of graph of GFlops vs. matrix size (as before, superimpose this graph on the graphs from (a) and (b)). Using PAPI counters, measure the L1 data-cache misses for the largest matrix size. Explain your results briefly.

(d) (30 points) Repeat (c), but this time, implement both register-blocking and L1 cache-blocking. You will have wrap three loops around the mini-kernel to get a full MMM. Use any method you wish to determine a good value for NB. Measure the GFlops you obtain for a range of matrix sizes, and plot of graph of GFlops vs. matrix size (as before, superimpose this graph on the graphs from the previous parts). Using PAPI counters, measure the L1 data-cache misses for the largest matrix size. Make sure you only use matrices whose size is a multiple of your choice of NB so you do not need to write clean-up code to handle fractional tiles.. Explain your results briefly.

(e) (15 points) You can improve the performance of your kernel by copying blocks of data into contiguous storage as explained in the Yotov et al paper. Implement data copying and produce the performance graph for this optimized code, superimposing it on the graphs from all the previous parts. Using PAPI counters, measure the L1 data-cache misses for the largest matrix size.

(f) (5 points) Use the Intel Math Kernel Library (MKL) to perform the matrix multiplications. You can see more information about Intel MKL here

Submission

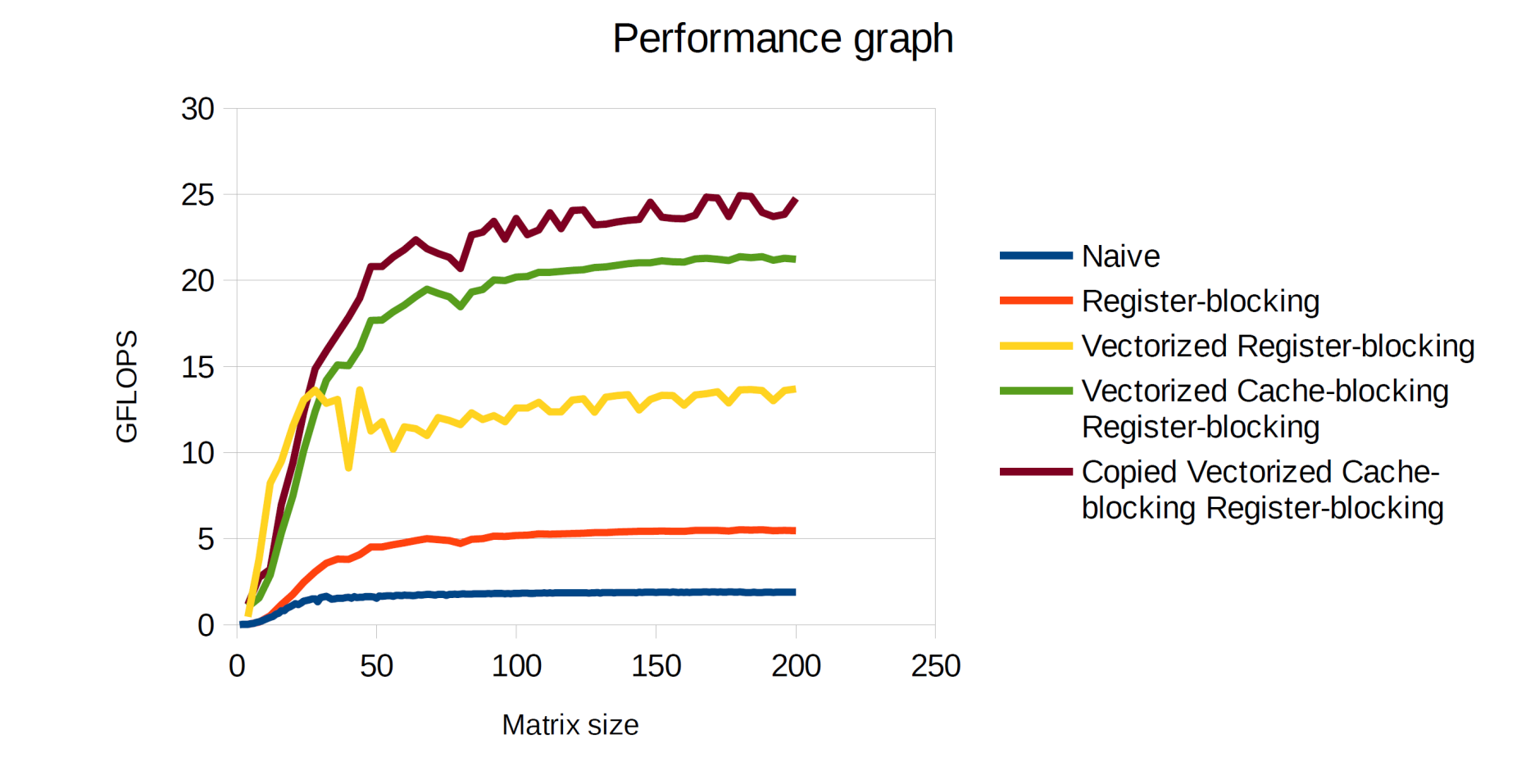
Submit your code, the write-up and the performance graphs. You can submit a single graph with all the plots, similar to the one shown below.

Implementation notes:

1) In the C programming language, a 2-dimensional array of floats is usually implemented as a 1-dimensional array of 1-dimensional arrays of floats. To reduce the possibility of conflict misses, it is better to allocate one contiguous block of storage to hold all the floats, and then create a 1-dimensional row vector that holds points to the start of each row. You can use the following code for this purpose: it takes the number of rows (x) and columns (y) as parameters, and it returns a pointer to the row vector.

 float **Allocate2DArray_Offloat(int x, int y)
{
           int TypeSize = sizeof(float);
           float **ppi   = malloc(x*sizeof(float*));
           float *pool   = malloc(x*y*TypeSize);
           unsigned char *curPtr = pool;
           int i;
           if (!ppi || !pool)
           {  /* Quit if either allocation failed */
                   if (ppi) free(ppi);
                   if (pool) free(pool);
                   return NULL;
           }
           /* Create row vector */
           for(i = 0; i < x; i++)
           {
                   *(ppi + i) = curPtr;
curPtr += y*TypeSize;
           }
           return ppi;
    }

2) Here is a nice paper on coding guidelines for writing "portable assembly language programs" in the C language.

3) You can also read an article about the GotoBLAS by Goto and van de Geijn.

4) To give you an idea of what to shoot for, here are some results we obtained for the different versions of MMM. Your mileage may vary but the trends should be similar. We have not shown the MKL line.