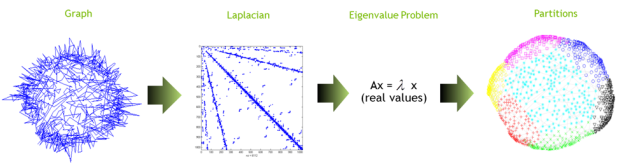
The overall idea of spectral approach is to build a matrix, solve an eigenvalue problem, and use eigenvectors for clustering/partitioning.
Project contacts: Sepideh Maleki, Udit Agarwal
Overview
Hypergraphs are a generalization of graphs where each edge (hyperedge) can connect more than two nodes. A hypergraph H = (V, E) consists of a set of nodes, V, and a set of hyperedges, E, where each hyperedge is a non-empty subset of V.
In this project we will study hypergraph bipartitioning, the problem of dividing a hypergraph into almost evenly sized disjoint pieces. Hypergraph partitioning is an active area of research, central to many VLSI, linear algebra, Boolean satisfiability, and data-mining algorithms.
There are many strategies to perform hypergraph partitioning, starting from local heuristics, such as Kernighan-Lin and Fiduccia-Mattheyses, to global spectral and multi-level techniques. In this project, we will focus on the global spectral graph partitioning technique. It constructs the Laplacian matrix and uses its smallest eigenpairs to perform the partitioning.
Goals
The overall idea of spectral approach is to build a matrix, solve an eigenvalue problem, and use eigenvectors for clustering/partitioning.

Specification
These are the steps for spectral partitioning:
Project deliverables and deadlines: