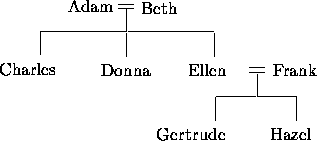
There are two basic operations on a knowledge-base -- queries and assertions . Queries generally retrieve knowledge from the knowledge-base, applying if-needed rules, while assertions generally add new facts to the knowledge-base and apply if-added rules. Of course, a successful if-needed rule will assert its consequent into the knowledge-base, and the antecedent of an if-added rule may have additional terms to be queried, so the two operations are not disjoint. Rules in Algernon are tied into the frames of the knowledge-base by being associated either with frames or with slots. To understand how this works, consider a knowledge-base of frames and rules representing the following genealogy:
Assume further that we have a frame People (representing the set
of all people) and that the relation isa
has been
asserted between the frames for the people in the genealogy and the frame
People (e.g., (isa Adam People), (isa Beth People),
). Assume further that the rule:
is associated with the frame People. Formally this means:
What this means operationally is that any query to the aunt slot of a frame that is an isa relation to the frame People will result in the application of this rule. Rules are applied by first querying their antecedent and then, if the antecedent succeeds, asserting their consequents. For example, if we query (aunt Hazel ?x) then the rule will apply, the access path will be followed (from Hazel to Ellen to Donna) and Algernon will conclude (and assert) (aunt Hazel Donna). However, if we query (aunt Charlie ?x) then the rule will fire, but the access path will ``dead-end'' (at Adam and Beth). Algernon will thus find no aunts of Charlie and the query is said to fail.
Rules may also (less commonly) be associated with slots or sets of slots. If an if-added rule is associated with a slot r, or with a set of which r is a member, then it is applied whenever a value is added to the r slot of any frame (if-needed rules associated with slots and sets of slots are similar). For example, one might want to put the slot less in the set of partial orders, and thus inherit rules, associated with the set of partial orders, for transitivity, reflexivity, and antisymmetry.