CS378: Concurrency

Lab #2

The goal of this assignment is to use thread-level parallelism, coarse, and fine-grain locking, as well as barrier synchronization to solve a classic data-parallel problem: K-means.

K-Means

K-Means is a machine-learning algorithm most commonly used for unsupervised learning. Suppose you have a data set where each data point has a set of features, but you don't have labels for them, so training a classifier to bin the data into classes cannot rely on supervised algorithms (e.g. Support Vector Machines, which learn hypothesis functions to predict labels given features).

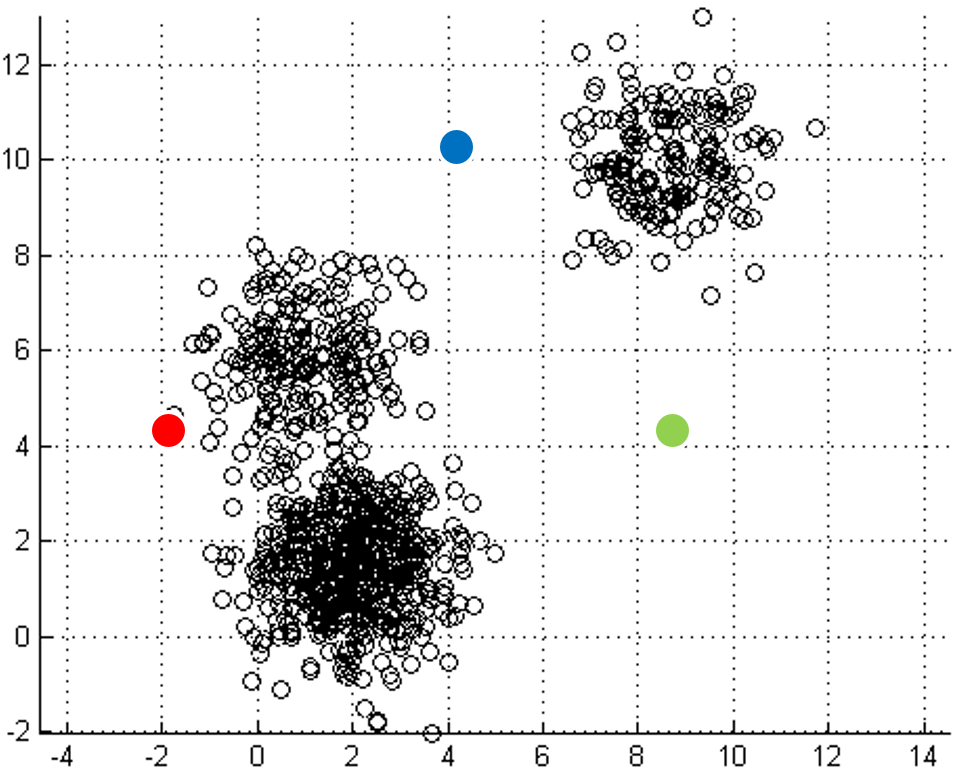
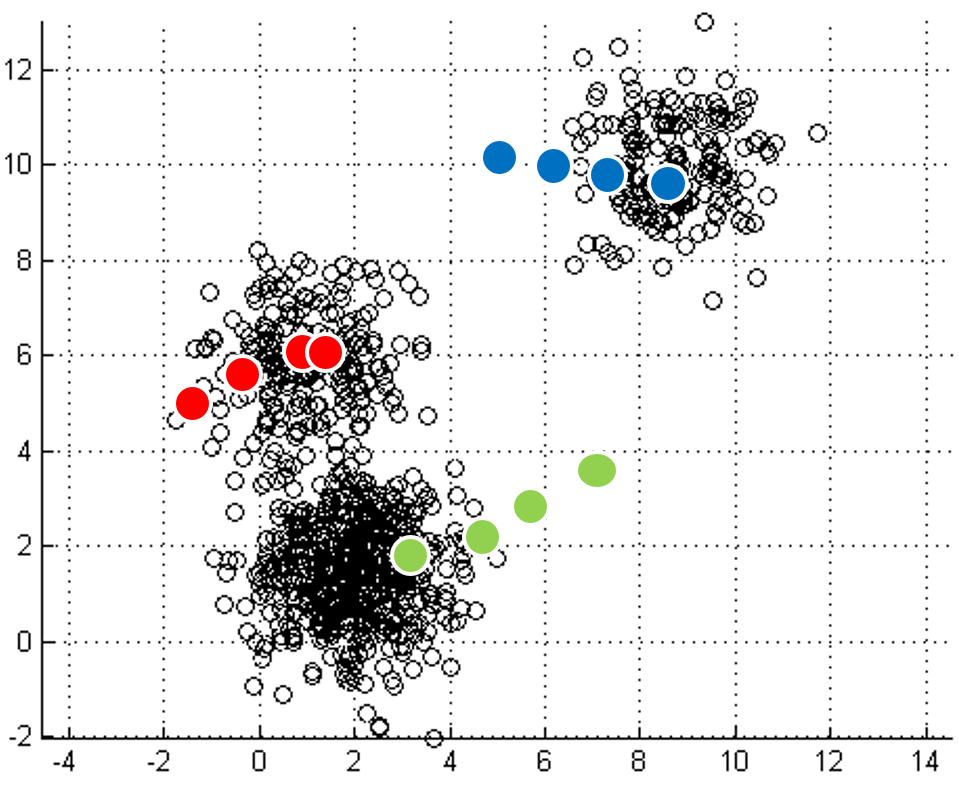
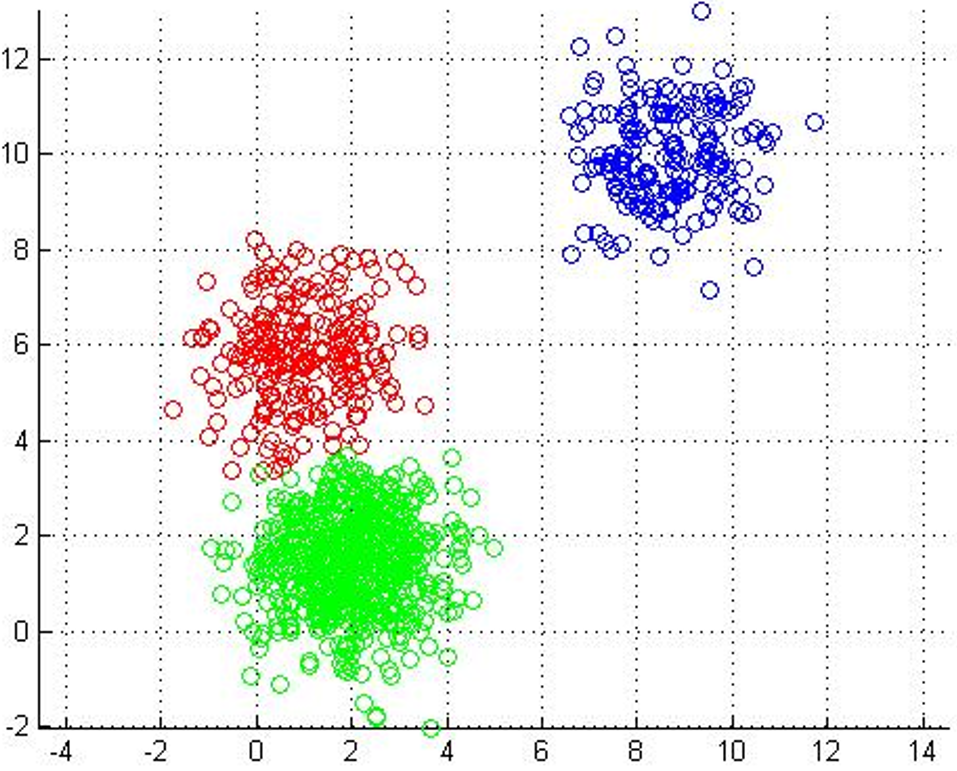
One of the most straightforward things we can do with unlabeled data is to look for groups of data in our dataset which are similar: clusters. K-Means is a "clustering" algorithms. K-Means stores k centroids that define clusters. A point is considered to be in a particular cluster if it is closer to that cluster's centroid than to any other centroid. K-Means finds these centroids by alternately assigning data points to clusters based on a current version of the centroids, and then re-computing the centroids based on the current assignment of data points to clusters. The behavior the algorithm can be visualized as follows:
Initial input Choose three random centers Map each point to its nearest centroid New centroid is mean of all points
mapping to it. Iterations move
the centroids closer to their destination.		 Centroids stop moving.
Each point labeled with its nearest centroid.

The Algorithm

In the clustering problem, we are given a training set x(1),...,x(m), and want to group the data into cohesive "clusters." We are given feature vectors for each data point x(i) encoded as floating-point vectors in D-dimensional space. But we have no labels y(i). Our goal is to predict k centroids and a label c(i) for each datapoint. Here is some pseudo-code implementing k-means: 

kmeans(dataSet, k) {

  // initialize centroids randomly
  numFeatures = dataSet.getNumFeatures();
  centroids = randomCentroids(numFeatures, k);

  // book-keeping
  iterations = 0;
  oldCentroids = null;

  // core algorithm
  while(!done) {

    oldCentroids = centroids;
    iterations++;

    // labels is a mapping from each point in the dataset 
    // to the nearest (euclidean distance) centroid
    labels = findNearestCentroids(dataSet, centroids);

    // the new centroids are the average 
    // of all the points that map to each 
    // centroid
    centroids = averageLabeledCentroids(dataSet, labels, k);
    done = iterations > MAX_ITERS || converged(centroids, oldCentroids);
}

The Implementation

We strongly recommend you do this lab using C/C++ and pthreads. However, it is not a hard requirement--if you wish to use another language, it is fine as long as it supports or provides access to thread management and locking APIs similar to those exported by pthreads: you'll need support for creating and waiting for threads, creating/destroying and using locks, and for using hardware-supported atomic instructions. Using language-level synchronization support (e.g. synchronized or atomic keywords) is not acceptable--it can preserve correctness obviously, but it sidesteps the point of the lab. You can meet these requirements in almost any language, but it is worth talking to me or the TA to be sure if you're going to use something other than C/C++.

Deliverables will be detailed below, but the focus is on a writeup that provides performance measurements as graphs, and answers (perhaps speculatively) a number of questions. Spending some time setting yourself up to quickly and easily collect and visualize performance data is a worthwhile time investment since it will come up over and over in this lab and for the rest of the course.

Step 1: Create a sequential solution

In step 1 of the lab, you will write a program that accepts command-line parameters to specify the following:

The output of your program should include:

For example, the following command-line invoked on zwerdling.cs.utexas.edu yield corresponding output in our sample solution: 

    ./kmeans --input kmeans-sample-inputs/color100 --workers 4 --threshold 0.0000001 --iterations 0 --clusters 4
    Converged in 19 iterations (max=0)
    parallel work completed in 811 usec
    Cluster 0 center: [-0.170][1.592][1.114][2.429][0.102][-3.015][-0.057][-0.483][-0.646]
    Cluster 1 center: [2.281][0.622][-1.899][-0.021][-0.907][-0.495][-0.168][-0.355][-0.116]
    Cluster 2 center: [0.520][0.867][-0.059][-0.157][0.343][0.065][-0.829][-0.159][0.538]
    Cluster 3 center: [2.359][1.081][-2.167][2.755][-0.030][-3.740][-0.737][-0.915][-0.222]

The --iterations and --threshold options have some nuance and should be given well-chosen defaults. The --iterations option specifies the maximum number of times the loop will run, even the clustering does not converge (MAX_ITERS) in the code fragment above. The --threshold option specifies the minimum euclidean distance between oldCenters and centers required for the algorithm to terminate. The --iterations option will operate as essentially just a fall-back mechanism to ensure termination in this lab: it's very useful for debugging. You should code your solution such that the default value of --iterations is 0, which will mean that MAX_ITERS isn't enforced. Your default value of --threshold should 0.0000001f.

While the options allow you to specify a number of workers, your initial solution should just implement a single-threaded version of the algorithm. This greatly simplifies debugging. More importantly, the single-threaded version will be the baseline against which to measure subsequent parallel versions.

Input files will follow the format below, where the first line specifies the integer valued number of points in the input, and each subsequent line describes a dim-dimensional point, and where each dimension's value is a floating point number. We recommend you use single precision float in your program rather than double but this is not a hard requirement. 

    <Number-of-points>
      1 <dim0-value> <dim1-value> ... <dim-(d-1)-value>
      2 <dim0-value> <dim1-value> ... <dim-(d-1)-value>
		  ...
      <Number-of-points>  <dim0-value> <dim1-value> ... <dim-(d-1)-value>
Samples can be found here, and we provide a generate.py utility to create your own inputs. Invoke generate.py with no command line options to see instructions for using the utility.

Step 2: Coarse Synchronization

K-means is a readily parallelizable algorithm, so there are many approaches to parallelizing it. The most straightforward, given the material we've seen so far in this class, is a bulk-synchronous parallelization (BSP) which forks some number of threads across which some partition of the input data set is partitioned. Your solution to lab0 may come in very handy at this point.

While partitioning the input across some number of threads is straightforward (be sure you handle corner cases where threads do not get an even partition of the input), you should find you need some synchronization to ensure that updates to the centroids are well synchronized. Assuming you do not spawn new threads for each iteration (you don't, right?), you additionally need some barrier synchronization at the beginning and end of each iteration to ensure that each thread is ready/done when you decide if the algorithm has converged. Your first parallelization should use a single lock to synchronize access to the cluster centers. We will compare performance when the the lock is implemented with pthread_mutex_t versus pthread_spinlock_t. You should ensure that each worker begins/finishes its iterations before the next iteration occurs using some number of pthread_barrier_t primitives.

Using the random-n65536-d32-c16.txt sample input, --iterations 20, --clusters 16, and --threshold 0.0000001, create a graph of speedup for pthread_mutex_t and pthread_spinlock_t for your solution from 1 to twice the number of physical processors on your machine for your solution at this step. Please normalize your measurements with the single-threaded solution from Step 1. This means that unlike in the first lab, where we simply reported execution time, your graph should be a speedup graph.

Step 3: Finer-grain Synchronization

Your solution in step 2 used locks over the centroids to synchronize updates from different threads. You may have found the scalability to be somewhat disappointing. In this step, you will additionally privatize your updates, so that each thread maintains private state during the bulk of the iteration, and requires synchronization only to add its partial aggregation of the data to the global update of the centroids.

Again using the random-n65536-d32-c16.txt sample input, --iterations 20, --clusters 16, and --threshold 0.0000001, Create another speedup graph like the one above, where pthread_mutex_t and pthread_spinlock_t primitives are used to synchronize en masse updates accumulated privately by each thread at the end of each iteration. Again your graph should be a speedup graph, where data are normalized to the single-threaded Step 1 case.

Step 4: Extra Credit: Finer grain synchronization

In this step, you may, for extra credit, explore other ways to make synchronization even finer grained to reduce contention and increase scalability. Can you use CAS-based updates? HTM? Does padding data structures to avoid false sharing have any impact on your performance? Locks per-dimension? Functional decomposition instead of domain decomposition? Extra credit will be given for any reasonable solution that undertakes this section, as long as the solution is still correct: trying to improve scalability is a worthwhile endeavor, even if you don't succeed. If you do this, include graphs, along with some conjectures about the performance behavior of your implementation. Major kudos (and major extra points) go to the solution that has fastest absolute performance and to the one that is most scalable (has closest to linear speedup).

Deliverables

Using the canvas turn in utility, you should turn in, along with your code, Makefiles, and measurement scripts, a brief writeup with the scalability graphs requested above. Be sure that your writeup includes sufficient text to enable us to understand which graphs are which. Note that as will other labs in this course we will check solutions for plagiarism using Moss.

A LaTeX template that includes placeholders for graphs and re-iterates any questions we expect answers for can be found here, (a build of that template is here).

Please report how much time you spent on the lab.

Acknowledgements

The description of k-means in this document draws heavily from one by Chris Piech. Thanks, Chris.

The sample inputs and generate.py utility are derived from artifacts in the STAMP benchmark suite. I've been using them for years: many thanks to Christos Kozyrakis and his students.