The goals of this assignment are:
In this assignment, you will implement a work-efficient parallel prefix scan algorithm using the pthreads library and a synchronization barrier you will write yourself. We encourage you to think carefully about the various corner cases that exist when implementing this algorithm, and challenge you to think about the most performant way to synchronize a parallel prefix scan depending on its input size.

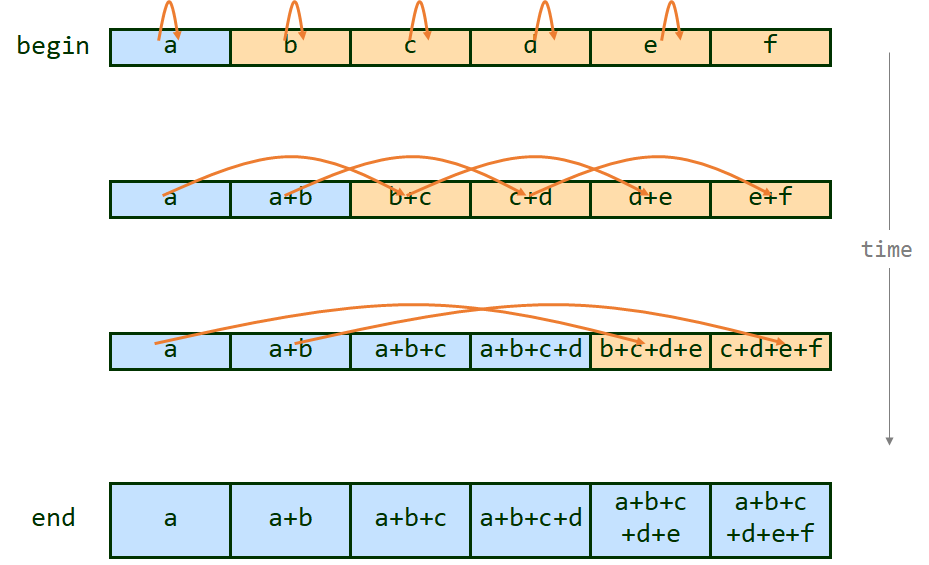
Parallel prefix scan has come up a number of times so far in the course, and will come up again. It is a fundamental building block for a lot of parallel algorithms. There are good materials on it in Dr. Lin's textbook, and the treatment of it you can find on Wikipedia comes with reasonable pseudocode (see here). You may notice that prefix sum and prefix scan are in fact the same, with sum just being a single instance of the associative and commutative operator that scan requires. Note that you will have the option of what parallel prefix sum algorithm to implement. The version we used in class to motivate barrier discussion is the Hillis-Steele algorithm, which has a lot of parallelism but is not work-efficient (meaning the number of scan operations it does is not in the same complexity class as the sequential prefix sum). The work efficient version, by contrast, is more efficient but exercises multi-core hardware in a fairly different way. Similarly there are variants like the 2-level method that change algorithm dynamically. You can implement any one you want as long as it attempts to take advantage of parallelism meaningfully, meaning there are fewer parallel steps than there would be sequential steps. Similarly, prefix sums can be inclusive or exclusive: since each can be trivially generated from the other, you can choose according to your own taste. If you implement more than one approach and compare performance in your report, extra credit will be awarded.
scan_op(x, y) function on each pair of items your code processes. Note that in
this snippet x and y can be of any type, so you will be required to write your prefix scan using
C++ generics and templated functions.
Your prefix scan will have to receive a type and a function pointer as template arguments. You will use the type parameter
to describe the types of x and y, and the function pointer to pass your implementation of
scan_op(x,y).
For each of the below steps, you will be comparing the performance of your prefix scan implementations by summing integers as well as high-dimensionality floating point vectors. You will only compare speedups between sums of values of the same type (i.e. sequential integer sums vs. parallel integer sums, not sequential integer sums vs. high-dimentionality FP vector sums).
The first step with any parallelization is to develop a sequential version to serve as a baseline both for performance and correctness.
It is generally easier to get the algorithm right without parallelism, and you need a sequential version anyway to measure against
so you can tell if your parallel implementation is performance-profitable. The command line parameters we would like your implementation
to support are listed in the "Inputs/Outputs" section below. We ask that you implement your sequential version
to be called when your program is invoked when the number of threads specified on the command line is 0 (-n 0). Note that
using a single pthread (-n 1) is not the same, as it involves all the overheads of thread creation and teardown that would
not be present in a truly sequential implementation.
Be sure your sequential implementation is correct before proceeding to parallelization!
Recall that prefix scan requires a barrier. In this step, you will write a work-efficient parallel prefix scan using pthread barriers. For each of the provided input sets, graph the speedup of your parallel implementation over a sequential prefix scan implementation as a function of the number of worker threads used. Vary from 2 to 32 threads in increments of 2. Then, explain the trends in the graph. Why do these occur? If your speedup is not ideal, what overheads are causing your implementation to underperform an "ideal" speedup ratio? Does summing integers in parallel yield greater speedup than summing floating-point vectors in parallel? Why or why not?
In this step you will build your own re-entrant barrier. Recall from lecture that we considered a number of implementation strategies and techniques. We recommend you base your barrier on pthread's spinlocks, but encourage you to use other techniques we discussed in this course. Regardless of your technique, answer the following questions: how is/isn't your implementation different from pthread barriers? In what scenario(s) would each implementation perform better than the other? What are the pathological cases for each? Use your barrier implementation to implement the same work-efficient parallel prefix scan. Repeat the measurements from part 2, graph them, and explain the trends in the graph. Why do these occur? What overheads cause your implementation to underperform an "ideal" speedup ratio?
How do the results from part 2 and part 3 compare? Are they in line with your expectations? Suggest some workload scenarios which would make each implementation perform worse than the other.
The first line of the input file will contain a single integer, x. If x = 0, the remainder of the file will contain only integers. If x > 0, then each line of input will contain x comma-separated floating point values (representing an x-dimensional floating point vector).
The second line in the input file will contain a single integer i denoting the number of lines of input in the remainder of the input file. The following i lines will each contain either a single integer or a comma-separated set of floating point values, representing one item in the input array. Your program should read in these i items, compute their prefix sums, and print the sums to the specified output file, with either a single integer or an x-dimensional vector on each line. Note: there should be i lines in your output file, each with either a single integer or a comma-separated list of floating point values.
Some sample inputs and a python script to generate your own test inputs can be found here: test_01.txt, test_02.txt, test_03.txt, test_04.txt.
Your source code should include a Makefile which produces your executable by simply running make in the top-level directory of your submission. The executable should be named "pfxsum" and must accept the above arguments exactly as they are described. It is critically important you follow the build conventions and command line requirements exactly, as we will test and measure your code using automated tools that expect your executable and command line options to be specifically as described above.
Your solution should output the execution time in seconds to stdout, and no other output. It is fine to produce other output on stdout as long as it is disabled by default, either at compile time (using macros) or at runtime (using an extra/optional command-line flag).
When you submit your solution, you should include the following:
Please report how much time you spent on the lab.