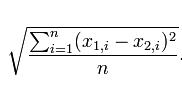CS 314 - Specification 11 - Graphs
Programming Assignment 11 - Individual
Assignment. You must complete this assignment on your own. You may not acquire
from any source (e.g. another student, an internet site, Large
Language Model or Generative AI such as chatGPT or Copilot) a partial or complete
solution to a problem or project that has been assigned. You may not show another student your
solution to an assignment. You may not have another person
(current student, former student, tutor, friend, anyone) “walk you through”
how to solve an assignment. You may get help from the instructional staff.
You may discuss general ideas and approaches with other students but you may not
develop code together. Review the class policy on collaboration
from the syllabus.
- Placed online: Tuesday, November 11
- Due: no later than 11 pm, Thursday, December 5 (You CAN use
slip days on assignment 11 if you have some left. Some semester do not allow the use of slip days
when the assignment is due the last day of class, but that is not the case
this term.)
- General Assignment Requirements
The purposes of this assignment are:
- implement two graph algorithms
- use graphs to rank college football teams based on the results from a
single season
Description: In this assignment you will implement two instance methods for
a graph class and one method in a client of the graph class that
evaluates properties of the graph.
When finished turn in your Graph.java, FootballRanker.java, and
GraphAndRankTester.java files.
Provided Files:
|
|
File |
Responsibility |
|
Documentation |
Documentation for the provided classes. |
Provided by me. |
|
Implementation |
Graph.java. A class that implements a Graph data structure. Complete the
two required methods, dijkstra and findAllPaths. |
Provided by me and you. |
|
Implementation |
FootballRanker.java.
A class that ranks football teams based on their performance using the
Graph class. Each team is a vertex. A directed edge exists between team
A and B if team A beat team B. The weight of the edge is determined by
the score of the game between teams A and B. The closer the score the
LARGER the weight. Complete the required method
printRootMeanSquareError. |
Provided by me and you. |
| Implementation |
GraphAndRankTester.java
A class that runs tests on the Graph and
FootballRanker classes. Add more tests to the class for the Graph class
and the FootballRanker class. Answer the question at the top of
GraphAndRankTester.java. |
Provided by me and you. |
| Provided Files |
FootballRecord.java A simple class for modeling the
win and loss record of a football
team.
AllPathsInfo.java A class with information about all paths from a given
vertex in a Graph to other vertices in the Graph.
These classes are used by Graph.java and FootballRanker.java |
Provided by me. Do not alter. |
| Data Files |
2008ap_poll.txt and
div12008.txt - The data files
that generate the sample output. The div12008.txt file contains the results of
all division I college football games from 2008 and
2008ap_poll.txt file contains the final division I Associated Press rankings for
2008.
2014ap_poll.txt
and div12014.txt -
Another set of data files. Run your program with these data files and
post results on the class discussion group to compare.
2005ap_poll.txt and
div12005.txt - Another
set of data files. Run your program with these data files and post
results on the class discussion group to compare. Finally here all games from 2008,
(games08.txt) not just the division 1 teams. Try your program on
this file and compare the results to those with just the division 1
teams. Some surprises occur. The question in GraphAndRankTester ask how to adjust results when all teams are included.
You may have to do some research on the various divisions of college
football in order to answer the questions. |
Provided by me. Do not alter. |
| Sample Output |
Sample output. Based on 2008 data. Your output must match this exactly. |
Provided my me. |
| All Files |
a11_all.zip All files in a
zip.
(If you would rather not download all of the files above separately.) |
Provided by me. |
| Submission |
Graph.java, FootballRanker.java, and GraphAndRankTester.java files. |
Provided by you.. |
Background: Prior to the 2014 season, division 1 college football
was one of the few college
sports where the champion was not determined by a tournament run by the NCAA.
Instead the BCS, the Bowl Championship Series, used various polls and surveys are used to determine the
"best" two teams who then played each other in the final game of the season.
The ranking algorithm the BCS used consisted of two human surveys PLUS six algorithms carried out by computers.
(Note, the algorithms used by the BCS were not allowed to take into account
the score of games, only whether a team won or lost a game. The people
running the BCS thought it
unsporting to encourage stronger teams to run up the score on weaker
teams.) As of 2017 division 1 college football uses a 4 team playoff at the
end of the season. The four teams are picked by a
committee of humans. The new selection committee claims to not use any
algorithms in determining its rankings. There are still a
large number
of individuals that publish ranking based on algorithms.
In this assignment
you will complete a Graph class and a FootballRanker class that determines
the "best" team based on the graph formed by the division 1
college football teams and the games they
played against each other.
Centrality of vertices
in the graph with some adjustments are used to determine the "best"
team. Your program shall rank teams three ways and compare the results
to the Associated Press end of season poll,
another poll completed by humans with no algorithmic input.
The three ranking algorithms for the assignment are:
- Rank each team by calculating the number of other teams they are connected
to and the average shortest UNWEIGHTED paths to those connected teams. Determine the average
UNWEIGHTED path length by dividing the total sum of all shortest, unweighted path
lengths (number of edges in path) by the number of vertices (teams) connected.
- Rank each team by calculating the number of other teams they are connected
to and the average shortest WEIGHTED path to those connected teams. Determine
the average WEIGHTED path length by dividing the total sum of all shortest, weighted path
lengths by the number of vertices (teams) connected.
- Rank each team using the result from method 2 and then dividing the average
weighted path length by the team's
win / loss percentage.
Most of the program is already done. There are three methods you
must complete are:
- Complete the instance method
dijkstra in the Graph class.
This method finds the shortest weighted path from the given start vertex to
all other vertices in the graph using Dijktsra's Shortest Weighted Path Algorithm. Read the method
documentation thoroughly to understand all the requirements of the method.
Recall the class slides contain the pseudocode for this algorithm.
- Complete the instance method
findAllPaths in the Graph class. This method
updates each vertex in the Graph so that each vertex stores
the number of other vertices it is connected to. (In the assignment this is
also referred to as the number of paths from the vertex.) The method also
finds the sum of all the shortest weighted and unweighted paths from the vertex
to every other vertex it connects to.
If the boolean parameter named weighted is false
these values will equal each other. Read the comments for the numVertexConnected, totalUnweightedPathLength, and totalWeightedPathLength
instance variables in the Vertex class to help understand the purpose of
findAllPaths.
Each Vertex object
has instance variables to store this data. The method must call the
findUnweightedShortestPath or dijkstra methods as
appropriate. The Vertex class, the nested Path
class, and the getPath(String) method are useful for
completing and testing this method. A lot of the support
code is already done for you. You must determine how to use the existing code.
You are of course, free to write you own support code if you prefer, but your
output must match the expected output.
The method also finds and stores the "longest shortest path" in the Graph. Because the
method must find the shortest path between all pairs of vertices relying on
the given findUnweightedShortestPaths method or the dijkstra
you complete based on the value of the parameter weighted, we can keep track
of the longest of the shortest paths we find. The length of the paths shall be
based on their weighted cost. For the findUnweightedShortestPaths
this is the same as the number of edges in the path. Use the getPath
method to create a Path object for the longest (highest cost)
path you find as you search the shortest paths. Use the instance variable
named longest to refer to this Path object.
Consider the following example:
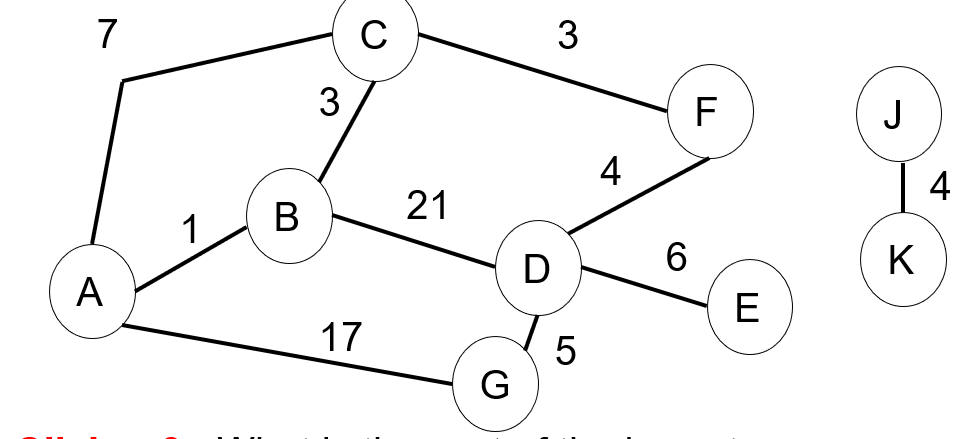
The graph is weighted, but
undirected. If we ran findAllPaths method and sent
false for weighted the cumulative sum statistics in the vertex
objects would be:
| Vertex |
numVertexConnected |
totalUnweightedPathLength |
totalWeightedPathLength |
| A |
6 |
10.0 |
10.0 |
| B |
6 |
9.0 |
9.0 |
| C |
6 |
10.0 |
10.0 |
| D |
6 |
8.0 |
8.0 |
| E |
6 |
13.0 |
13.0 |
| F |
6 |
10.0 |
10.0 |
| G |
6 |
10.0 |
10.0 |
| J |
1 |
1.0 |
1.0 |
| K |
1 |
1.0 |
1.0 |
If we ran findAllPaths method and sent true
for weighted the cumulative sum statistics in the vertex objects would be:
| Vertex |
numVertexConnected |
totalUnweightedPathLength |
totalWeightedPathLength |
| A |
6 |
20.0 |
56.0 |
| B |
6 |
15.0 |
51.0 |
| C |
6 |
12.0 |
42.0 |
| D |
6 |
12.0 |
43.0 |
| E |
6 |
17.0 |
73.0 |
| F |
6 |
11.0 |
39.0 |
| G |
6 |
17.0 |
68.0 |
| J |
1 |
1.0 |
4.0 |
| K |
1 |
1.0 |
4.0 |
- Complete the
printRootMeanSquareError method in the
FootballRanker class. The FootballRanker class computes
rankings for teams based on the three approaches described above. This method
relies on the findAllPaths method which in turn relies on the dijkstra
method, so you must complete those two methods before this one will work
properly. The printRootMeanSquareError method
in the FootballRanker compares the computed rankings from findAllPaths
with the end of season poll from the Associated Press. The AP's ranks are
stored in
list parameter sent to this method (position in list is equivalent to rank
when using zero based indexing) and the graph ranks are in the TreeSet. Iterate
through the AP ranks and determine the root mean square error between
the AP ranks and the calculated ranks. The root mean square error is determine
by taking the difference between the AP rank and the predicted rank, squaring
the difference, adding all of these squared differences together, dividing by
the number of teams, and taking the square root. The mathematical formula:
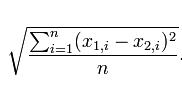
where, n is the number of teams, x1 is the AP rank for the ith ranked team, x2
is the predicted rank for that team based on our graph calculations for the
ith team, and n is
the number of teams. If a team is ranked in the AP poll, but not in our
predictions assign it a rank equal to one more than the total number of teams
in the graph predictions. (The FootballRanker cuts some teams from the
predictions if they do not have enough direct or transitive wins. (wins based
on connections in the graph)). The method prints out the data as shown in the
sample output and returns the root mean square error rounded to the nearest
tenth.
Your class must pass the tests in GraphAndRankTest class.
Add your own tests to the GraphAndRankTest class and delete the
provided tests so the TAs only see your tests.
Answer the question at the top of the GraphAndRankTest class. (Put
some thought into this.) If you are not familiar with the structure of the
college football system in the US you may have to do some
research. It is helpful to understand
the divisions
within college football.
Checklist: Did you remember to:
- review and follow the general assignment requirements?
- work on the assignment individually and not use any LLM and / or
chatbot such as chatGPT or Copilot?
- fill in the headers in your Graph.java, FootballRanker.java, and
GraphAndRankTester.java
- ensure program passes the provided tests and matches the sample output
exactly?
- add you own tests to GraphAndRankTester and delete the provided tests?
- answer the question at the top
of the GraphAndRankTester class?
- ensure your program does not suffer a compile error or runtime error?
- turn in the three required files (Graph.java, FoorballRanker.javam and
GraphAndRankTester.java) to the proper GradeScope assignment (#11)
no later than 11 pm, Thursday, December 5?