Combinatorial filter minimization
Description:
Combinatorial filters are discrete state transition structures for modeling and
reasoning about robotic systems. Each combinatorial filter reads a sequence of
measurements (also called observations) as input, and transitions to an
internal state, and then yields the outputs of that state. In this project, we
are interested in minimizing a combinatorial filter (also called the input
filter). In other words, the minimizer, with the minimum number of states,
should give a correct output for every string that can be traced in the input
filter.
For example, consider the safari park with vehicle rental service shown in Figure 1. The cars for hire are each equipped with a compass and an intelligent gear shifting system. The compass measures the heading of the vehicle before and after its movement, e.g., 'nw' means that the vehicle was heading north and then turned to face west. The intelligent gear shifting system takes the readings from the compass as input, and automatically shifts gears to abide with the speed limit. There are three types of speed limits on roads: (a) between 15 and 30 (gray), (b) speeds blow 30 (brown), or (c) slower than 15 (green). Every vehicle is capable of moving with a slow gear to drive with a maximum speed of 15, and with a high gear to drive between 15 and 30. A naïve gear shifting system satisfying the speed limits is realized by a filter shown in Figure 2: each vertex represents a system state, each edge represents the state transition, with the labels on the edges representing the readings from the compass. A vertex is colored gray if the system outputs high gear, colored green if it outputs low gear, or colored both colors if the system may use either gear (via, say, a non-deterministic choice). We want to find a minimal filter, like the one shown in Figure 3, that realizes appropriate behavior but fewest states.
For example, consider the safari park with vehicle rental service shown in Figure 1. The cars for hire are each equipped with a compass and an intelligent gear shifting system. The compass measures the heading of the vehicle before and after its movement, e.g., 'nw' means that the vehicle was heading north and then turned to face west. The intelligent gear shifting system takes the readings from the compass as input, and automatically shifts gears to abide with the speed limit. There are three types of speed limits on roads: (a) between 15 and 30 (gray), (b) speeds blow 30 (brown), or (c) slower than 15 (green). Every vehicle is capable of moving with a slow gear to drive with a maximum speed of 15, and with a high gear to drive between 15 and 30. A naïve gear shifting system satisfying the speed limits is realized by a filter shown in Figure 2: each vertex represents a system state, each edge represents the state transition, with the labels on the edges representing the readings from the compass. A vertex is colored gray if the system outputs high gear, colored green if it outputs low gear, or colored both colors if the system may use either gear (via, say, a non-deterministic choice). We want to find a minimal filter, like the one shown in Figure 3, that realizes appropriate behavior but fewest states.
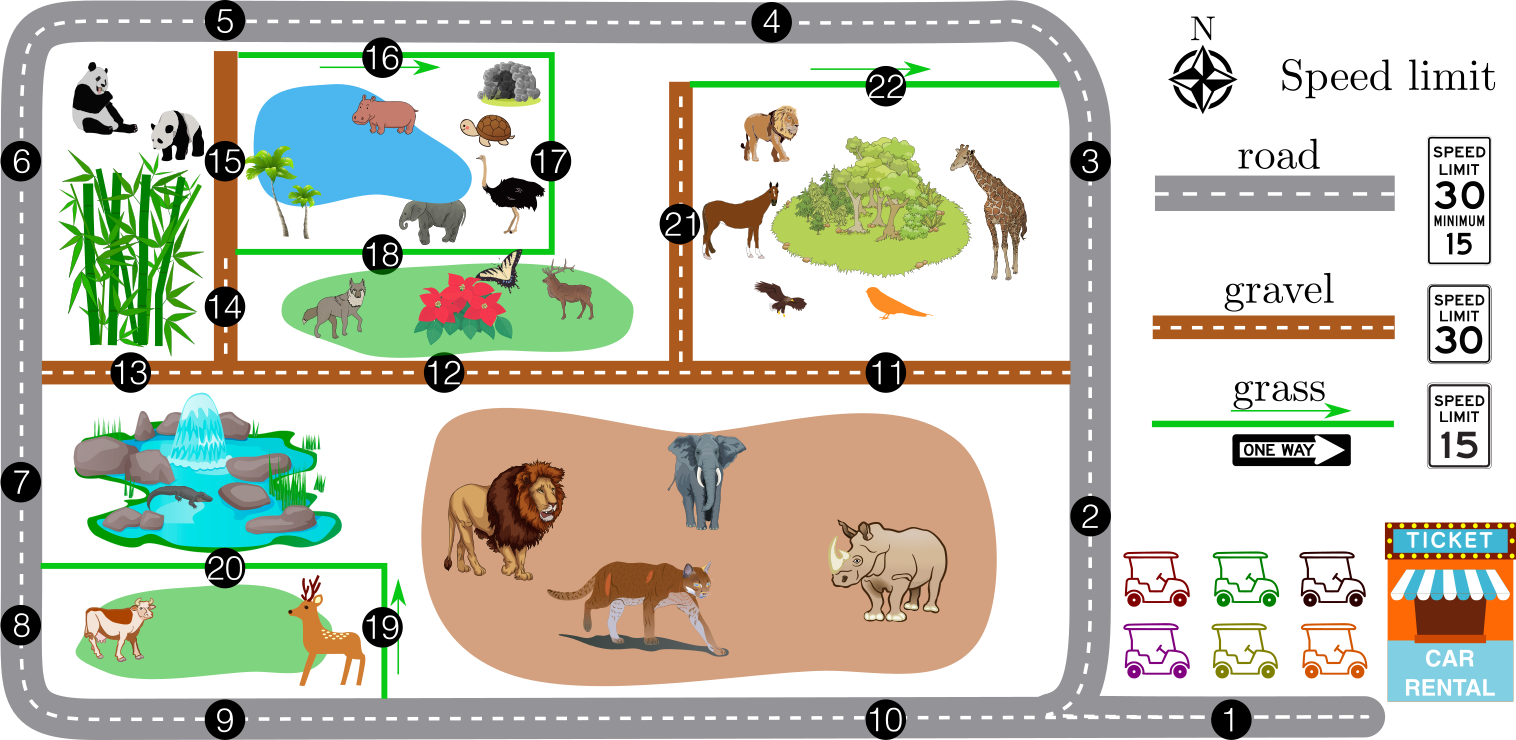
Figure 1: A safari park with vehicles for rental. The vehicles are equipped
with a compass to measure the heading of the vehicle, and runs an intelligent
gear shifting system automatically shifts the gear to satisfy the speed limit
according to its compass readings.
Figure 2: A naïve filter.
Figure 3: a minimal filter.
[1] Yulin Zhang, Dylan A. Shell. Nondeterminism subject to output commitment in combinatorial filters. International Workshop on the Algorithmic Foundations of Robotics (WAFR), 2022.
[arXiv]
[2] Yulin Zhang, Dylan A. Shell. On nondeterminism in combinatorial filters. IEEE International Conference on Robotics and Automation (ICRA), 2022.
[arXiv]
[3] Yulin Zhang, Hazhar Rahmani, Dylan A. Shell, Jason M. O'Kane. Accelerating combinatorial filter reduction through constraints. IEEE International Conference on Robotics and Automation (ICRA), 2021.
[arXiv]
[4] Yulin Zhang, Dylan A. Shell. Cover combinatorial filters and their minimization problem. International Workshop on the Algorithmic Foundations of Robotics (WAFR), 2020.
[arXiv]