Unit 2.2.1 Basic idea
¶Remark 2.2.1.
If the material in this section makes you scratch your head, you may want to go through the materials in Week 5 of our other MOOC: Linear Algebra: Foundations to Frontiers.
Key to understanding how we are going to optimize matrix-matrix multiplication is to understand blocked matrix-matrix multiplication (the multiplication of matrices that have been partitioned into submatrices).
Consider \(C := A B + C \text{.}\) In terms of the elements of the matrices, this means that each \(\gamma_{i,j} \) is computed by
Now, partition the matrices into submatrices:
and
where \(C_{i,j} \) is \(m_i \times n_j \text{,}\) \(A_{i,p} \) is \(m_i \times k_p \text{,}\) and \(B_{p,j} \) is \(k_p \times n_j \text{,}\) with \(\sum_{i=0}^{M-1} m_i = m \text{,}\) \(\sum_{j=0}^{N-1} n_i = n \text{,}\) and \(\sum_{p=0}^{K-1} k_i = k \text{.}\) Then
Remark 2.2.2.
In other words, provided the partitioning of the matrices is "conformal," matrix-matrix multiplication with partitioned matrices proceeds exactly as does matrix-matrix multiplication with the elements of the matrices except that the individual multiplications with the submatrices do not necessarily commute.
We illustrate how to block \(C \) into \(m_b \times n_b\) submatrices, \(A \) into \(m_b \times k_b \) submatrices, and \(B \) into \(k_b \times n_b \) submatrices in Figure 2.2.3

An implementation of one such algorithm is given in Figure 2.2.4.
void MyGemm( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int j=0; j<n; j+=NB ){
int jb = min( n-j, NB ); /* Size for "fringe" block */
for ( int i=0; i<m; i+=MB ){
int ib = min( m-i, MB ); /* Size for "fringe" block */
for ( int p=0; p<k; p+=KB ){
int pb = min( k-p, KB ); /* Size for "fringe" block */
Gemm_PJI( ib, jb, pb, &alpha( i,p ), ldA, &beta( p,j ), ldB,
&gamma( i,j ), ldC );
}
}
}
}
void Gemm_PJI( int m, int n, int k, double *A, int ldA,
double *B, int ldB, double *C, int ldC )
{
for ( int p=0; p<k; p++ )
for ( int j=0; j<n; j++ )
for ( int i=0; i<m; i++ )
gamma( i,j ) += alpha( i,p ) * beta( p,j );
}
Gemm_PJI which in this setting updates a \(m_b \times n_b \) submatrix of \(C \) with the result of multiplying an \(m_b \times k_b \) submatrix of \(A \) times a \(k_b \times n_b \) submatrix of \(B
\text{.}\)
Homework 2.2.1.1.
In directory Assignments/Week2/C, examine the code in file Assignments/Week2/C/Gemm_JIP_PJI.c. Time it by executing
make JIP_PJIView its performance with
Assignments/Week2/C/data/Plot_Blocked_MMM.mlx
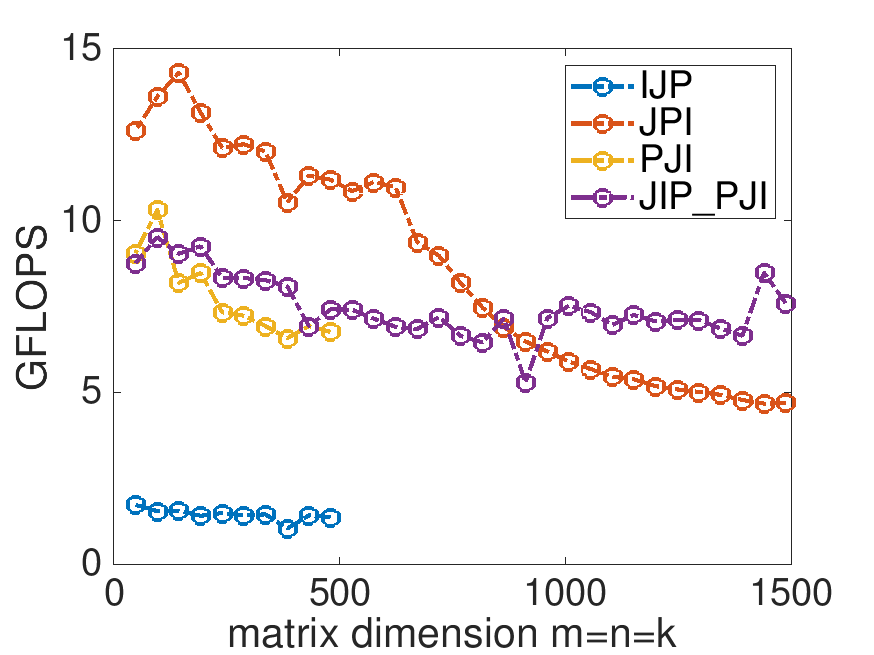
When MB=4, NB=4, and KB=4 in Gemm_JIP_PJI, the performance looks like
Homework 2.2.1.2.
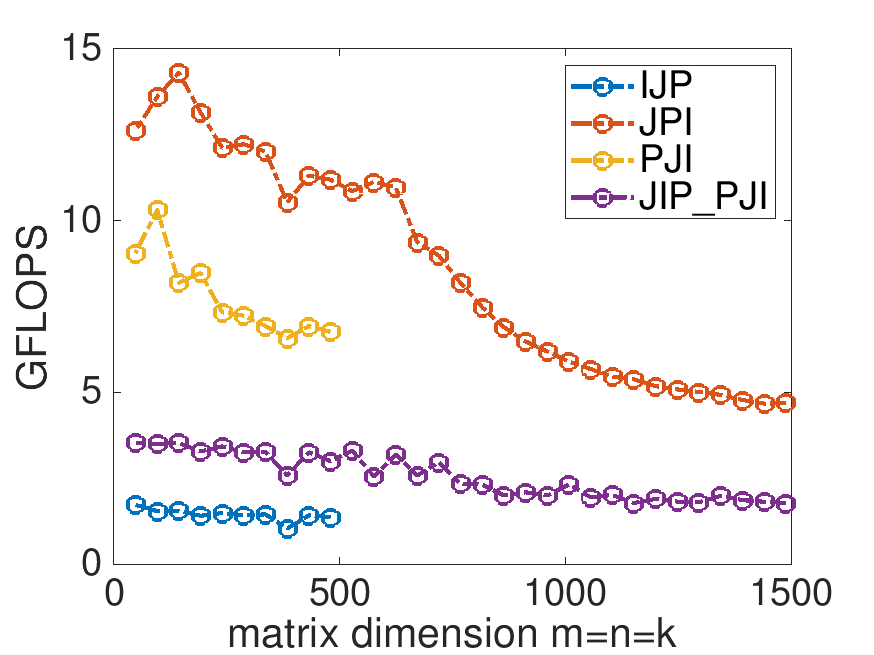
Examine the graph created by Plot_Blocked_MMM.mlx. What block sizes MB and NB would you expect to yield better performance? Change these in Gemm_JIP_PJI.c and execute
make JIP_PJIView the updated performance with
Assignments/Week2/C/data/Plot_Blocked_MMM.mlx (Don't worry about trying to pick the best block size. We'll get to that later.)
When we choose MB=100, NB=100, and KB=100 better performance is maintained as the problem size gets larger: