On notation

We have two main reasons for writing this note.

The one reason lies in the – if you come to think about it strange – coexistence of two circumstances. The one circumstance is that in a lot of mathematical work the use of an appropriate notation makes all the difference, notwithstanding Gauss even between feasibility and nonfeasibility. The other circumstance is that texts that give guidance in the conscious choice or design of appropriate notations are extremely rare. The regrettability of this state of affairs is amply confirmed by the mathematical literature, existing or being produced, of which notational clumsiness is an outstanding feature.

The other reason lies in a personal circumstance, viz. that all sorts of formula manipulation are beginning to play a more preponderant rôle in our derivations of proofs and programs. Thus we are frequently confronted with the inadequacy of existing notations and the need to design our own.

Remark. We are fully aware of the price of and resistance to change of widespread notations: the characterization of Florian Cajori’s encyclopedia as “a graveyard of notations” is more than appropriate. Hence we fully understand that, according to the morals of the bestseller society, notational experiments are considered a waste of time. We also know, however, the impossibility of progress without change and have found ourselves compelled to distinguish sharply between “convenient” and “conventional,” even if only for our own work. (End of Remark.)

In the past we have often missed guiding principles for the design of notations; the purpose of this note is to alleviate this deficiency. We tried to do so before, but the effort petered out before we had succeeded in raising our text above the level of motherhood statements. In retrospect we can see that at the time we lacked the varied calculational experience required. We are aware of having this time a broader overview of the purposes to be served by a good notation. We are also encouraged by recent experiences in which we suddenly found ourselves able to be much more specific and explicit than before in explaining the why and how of all sorts of derivations. Therefore we are this time not without hope.

*                       *
*

The purpose of this section is to delineate our topic.

Our starting point is that the notation used should be geared to the manipulative needs at hand. Sound and fruitful though this principle is, it is no good before the mechanisms available for manipulation have been specified. For instance, mechanized formula manipulation as performed in computers is most likely to use notations – e.g. combinator graphs – most unsuitable for manipulation with pen and paper. The latter even distinctly differs from the blackboard operated upon with a piece of chalk in the one hand and an eraser in the other: the almost continuous evolution of the text on the blackboard is all but impossible to capture in writing (as anyone can testify who ever tried to make notes of a lecture presented in such a fashion.)

The choice has to be made and we have decided to confine ourselves to the medium of pen and paper. This restriction of the topic creates specific opportunities and obligations. Among the opportunities we mention that paper – at least our paper – has room for more characters than an overheat sheet displayed before a large spectatorship. Among the obligations we mention the introduction of ways for avoiding lengthy repetitions. (In computerized formula manipulation the problem is solved by the combination of pointers and garbage collection; with eraser and chalk the problem is circumvented.)

This choice having been made, we shall allow ourselves – if the need arises – to take into account that the pen is held by a hand and the text is to be seen by eyes. For instance, if “officially” a mathematical formula is nothing but a finite string of symbols, matters of layout are “officially” irrelevant; yet we all know that for somewhat longer formulae some visual aids to parsing make all the difference.

We might add that we consider pen and paper one of the serious tools of the working mathematician, a tool whose proper usage should be taught. We know that in many mathematical circles formal methods have a bad name, such as being laborious and error-prone. We find the judgement little convincing, as in the same circles often the simple hand-eye coordination that is required to manipulate formulae is lacking . Similarly we challenge the belief that careful presentation of formulae matters only in the final stage of print and publication, but that one’s scribbling-paper is above the law in the sense that there syntactic ambiguities and all other sorts of notational atrocities are permissible. We hold the view that those who habitually make a mess of their scribbling-paper deny themselves a valuable tool. In this respect our concerns go beyond those of the well-known paper by Halmos, which is exclusively concerned with preparing manuscripts for publication.

For the sake of clarity we shall keep those considerations that can be considered purely psychological separated from clearly technical considerations.

*                       *
*

This section is devoted to a survey of the purposes that in our view a notation should serve. We follow Whitehead who writes: “[Symbolisms] have invariably been introduced to make things easy. [...] by the aid of symbolism, we can make transitions in reasoning almost mechanically by the eye, which otherwise would call into play the higher faculties of the brain. [...] Civilization advances by extending the number of important operations which we can perform without thinking about them.”

The purpose of symbolisms is to guide the development of arguments and to facilitate their a posteriori validation. The purpose of notation is to contribute to these goals. At this stage it would be a bit premature to analyze how design and development can be guided by symbolisms; it is safe, however, to conclude that validation (and design) are facilitated by brevity of the text and modesty of the body of rules of manipulation.

We mention these two, brevity of the text and modesty of the rules, explicitly because in the past they have been in conflict. Because the formal texts were more visible, more tangible so to speak, than the rules of manipulation – which under the slogan “you know what I mean” were largely left implicit – , marginal reductions of text length have crept in at the expense of unmanageable complification of the rules of manipulation. When a little further on Whitehead writes: “Mathematicians have chosen to make their symbolism more concise by defining xy to stand for x ⋅ y.”, our comment is that the mathematicians probably made a mistake.

Remark. Half of Whitehead’s motivation for conciseness of the text is the enable formulae to be “rapidly written”. We consider this a telling misjudgement of the ergonomics of doing mathematics with pen and paper. In teaching how to use pen and paper well, the first thing we would teach would be to write slowly. It helps prevent writing errors and discourages “formal verbiage”. Furthermore, with any reasonably effective formalism, deciding what to write down is the main job that takes the time, not the physical act of writing. If it complicates the rules, reducing text length by a factor close to 1 is penny-wise and pound-foolish. (End of Remark.)

The moral of the above is twofold. Firstly, in judging a notational convention we shall give due weight to the consequences of its incorporation for the rules of manipulation. Secondly, we shall be on the look-out for ways of achieving brevity that are less complicating and preferably an order of magnitude more effective than the introduction of invisible operators.

This is the place to point out that an unfortunate notation can harm manipulation in a variety of ways.

• It can make manipulation merely clumsy. Roman numerals are the prime example. Another example is provided by all conventions in which the representation of a component – such as a subexpression – of a structure depends on the position the subcomponent occupies in that structure; they levy a heavy tax on the substitution of expressions for variables.

• It can introduce ambiguities as a result of which the rules of manipulation defy formulation. This is, for instance, the case if identity or scope of dummy variables is subject to doubt. Another example is provided by the coexistence of sequence “expressions” such as (1, ..., k) and (x1, ..., xk): with k = 2, x1 = 1, and x2 = 7, the latter “expression” can stand for the sequence (1, 2, 3, 4, 5, 6, 7) or the sequence (1, 7).

• It may lack the combinatorial freedom required. Since negation is its own inverse, it pairs propositions. Using the one-to-one correspondence between small and capital letters, Augustus de Morgan decided to denote the negation of Q by q. But the convention fails to cover the negation of expressions. As a result the formulation of the rule ¬ (p ⋁ q) ≡ ¬p ⋀ ¬q becomes a pain in the neck. (One has to resort to manoeuvres such as “if r ≡ p ⋁ q then R ≡ P ⋀ Q.” Had his notation been more adequate, de Morgan would probably not have gained immortality by his Law.) (End of • .)

Unfortunate notation can also be detrimental to brevity in a variety of ways.

• A notational convention may easily introduce parameters that are superfluous in the sense that they are constant all through the argument (which means that the flexibility provided by the parameter mechanism is not needed). If x1, ..., xk were our only way of denoting sequences, we would always have to drag the sequence length around.

• Lack of a mechanism for abbreviation may lengthen a text considerably. It may, for instance, be very helpful to be able to declare only once for the whole argument that such and such quantifications are over such and such ranges.

• Notational conventions may force the introduction of names, and this in turn may induce otherwise avoidable case analyses. (We know from English the difficulty of referring to a person without mentioning his or her sex.) If, in reference to Δ ABC, we encounter the ominous “Without loss of generality we can assume edge AB to be ...”, the angles have probably been named prematurely. The notation “Δ ABC” precludes anonymous angles.

• A notational convention may be combinatorially defective. For some predicate B a set of integers is defined by {i | B.i}. In the convention used, i has a double rôle, viz. it is the dummy and it denotes the element. To denote the set obtained from the previous one by squaring each element, one now has to go through contortions like {j | (E i ∷ j = i2 ⋀ B.i)}.

• Texts can easily be lengthened considerably by a failure to introduce the proper operators. Boolean equivalence and function composition come to mind. Another example is failure to recognize pair-forming as an operator over which quantifications distribute. The penalty for this is the impossibility of rewriting the long formula

((A X, Y : [f.X.Y] : X), (A X, Y : [f.X.Y] : Y))

as

((A X, Y : [f.X.Y] : (X, Y)) .

(End of • .)

Thus we have set the scene for a more detailed analysis of specific notational conventions.

*                       *
*

Because of the central rôle of formulae, let us start with grammatical questions. Formal grammars are used to define which strings of symbols are syntactically correct formulae, but that is only a minor part of the story.

The major rôle of formal grammars is to provide a recursive definition of a class of objects that, for lack of a better name, we might call “syntactic trees” (i.e. trees with subtrees labelled as syntactic units, or something like that). In passing they provide rules for representing each syntactic tree by a string of characters, called a formula. The reason for stressing the syntactic trees is that the major manipulations, such as substitution and replacement, are more readily defined in terms of syntactic units than in terms of string manipulation.

The view that we manipulate syntactic trees by manipulating formulae, gives rise to all sorts of considerations.

For instance, a grammar is called ambiguous if different syntactic trees are represented by the same formula. (Vide sin2x versus sin-1x.) Though common in practice, the adoption of ambiguous grammars is hardly to be recommended. (We can even strengthen the advice: not only should a grammar be unambiguous, but its nonambiguity should be simple to establish. The advice is based on the combination of two circumstances. Firstly, in order to accommodate special notational needs one must be willing to incorporate local extensions of the grammar. Secondly, nonambiguity can easily become tough to establish: do not set your hopes on “tools”, for in it full generality the problem is undecidable.)

Nonambiguity, however, is not the only issue; simplicity of the parsing algorithm is another one. A subexpression is always replaced by something of the same syntactic category, which implies that the working mathematician is parsing his formulae all the time and that, consequently, a complicated parsing algorithm increases his burden. (In the sixties, the parsing problem was studied well beyond our needs: for a well-designed programming language, the parsing problem should be trivial, not so much for the benefit of the compiler writer as for that of the programmer that is going to use the language. The promotion of a grammatical monstrum like Ada is a clear example of an ill-directed effort at user-friendliness, for which the DoD will pay heavily.)

This is probably the place to point out that the introduction of infix operators is a common technique of complicating the parsing problem, the trouble of infix operators being that they invite the introduction of priority rules so as to reduce the number of parentheses needed. When introducing an infix operator one faces the methodological problem that a lot of clairvoyance about its future usage is required to determine which priority will reduce the number of parentheses most effectively. (We warn the reader that beginning by leaving the priority undecided and ending up with ambiguous formulae is a common error.) A nuisance of priority rules is that they complicate parsing and, hence, substitution – substitute in the product x ⋅ y the sum 2 + 3 for x –; perhaps this complication is too slight to worry about, but it can never hurt to remember that it is there.

Infix notation has a definite charm for all associative operators, such as addition, multiplication, conjunction, disjunction, equivalence, minimum, maximum, concatenation, relational or functional composition, etc. . It is so much nicer to write

a max b max c

than

max(a, max(b, c)) or max(max(a, b), c) .

The obvious disadvantage of the latter notation is that it forces one to make a totally irrelevant decision. If one prefers a functional notation, max ⋅ (a, b, c) – i.e. a function on a nonempty list – is preferable.

The above example draws attention to another phenomenon. Besides being associative, max is also symmetric, and regrettably there is no really nice linear representation of the enumerated unordered pair. Whether we like it or not, we are forced to mention the elements in some order. The best we can do is to give the elements positions as similar as possible. The worst one can do is to hide the symmetry, as has happened in the notation for the binomial coefficients. With an alternative notation P.(i, j) – “P” from “Pascal” – defined on a pair of natural numbers by

P.(i, j) = if i = 0 ⋁ j = 0 ⇒ 1
              ⫾ i > 0 ⋀ j > 0 ⇒ P.(i-1, j) + P.(i, j-1)
              fi               ,

i.e. with P.(i, j) for 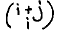and 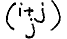, we can write

(x + y)n = (S i, j : i + j = n : P.(i, j) ⋅ xi ⋅ yj) .

Simplification of other formulae involving 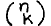is left as an exercise for the reader.

In this connection we note that symmetry considerations apply to operators as well. The beautiful symmetry of

            (P ⋀ Q) ⋁ (Q ⋀ R) ⋁ (R ⋀ P)
         ≡ (P ⋁ Q) ⋀ (Q ⋁ R) ⋀ (R ⋁ P)

is lost when we give conjunction a greater binding power than disjunction and write

            P ⋀ Q ⋁ Q ⋀ R ⋁ R ⋀ P
         ≡ P ⋁ Q ⋀ Q ⋁ R ⋀ R ⋁ P

But the question is more serious than that, because from here it is only a small step to the convention adopted in electrical engineering, where this formula would be rendered as

PQ + QR + RP = (P + Q)(Q + R)(R + P)     :

Conjunction’s distribution over disjunction is then rendered by

P(Q + R) = PQ + PR     ,

which looks very familiar; the other distribution, however, yields

P + QR = (P + Q)(P + R)     ,

which looks a bit strange. As a result, and as is to be expected, many an electrical engineer, though thoroughly familiar with the first distribution, is not so sure at all about the second one, and that psychological consequence of a mere notational convention could be deemed serious. In short, one has to decide whether saving a few parentheses is worth the price of destroying symmetry.

The common overloading of the plus and minus signs, which are unary and binary, should be a point of grammatical concern as well; it is in a way okay in infix notation, but defies the transition to post- or prefix notation. The effort of saving the unary additive operators by the invention of the invisible operand 0 makes matters only worse. In ALGOL 60, the invisible statement “skip” was introduced; subsequently, for “if B then S else” the abbreviation “if B then S” was allowed, and as a consequence

if B0 then if B1 then S0 else S1

was syntactically ambiguous. Seven centuries after the introduction of Hindu/Arabic numerals in the Western world, the ALGOL Committee should have known better.

A further grammatical concern is whether to keep the parsing algorithm context-free, i.e. to keep the parsing independent of the types of the operands.

For instance, anyone working with logical formulae in which relations between integers occur as boolean primaries, will be tempted to give those relational operators greater binding power than the logical operators. He will also be tempted to give equivalence a binding power lower than almost all other logical operators. Do we need a special symbol, say ≡, for equivalence or will the normal equality sign do? If we choose the equality sign, we either have to be willing to use more parentheses or have to resort to a context-dependent grammar. The latter alternative should not be adopted without full awareness of the price to be paid. Besides complicating the demonstration that the formalism is unambiguous – a demonstration which is required at each (even temporary) extension of the formalism – it places a burden on the use of the formalism: firstly, a formula like

                 a = b ⋀ c

cannot be read without an awareness of the types of the operands, and, secondly, types that can no longer be inferred from the formal context, have to be declared explicitly.

The most common way, however, of introducing context-dependent parsing – if not downright ambiguity – is the introduction of invisible operators, which results in a severe overloading of juxtaposition. The most common candidates for omission seem to be multiplication, concatenation, conjunction, and function application. The omission has all sorts of consequences.

Compare 3x, 3½, and 32. We are all so used to these that we hardly notice the anomaly any more. (In the “real world”, we have seen a recipe being misinterpreted: “11/2 cups of water” was read as 5.5 instead of 1.5. The result was desastrous.) But it becomes a different matter when we realize the massive amount of time spent on these in classrooms all over the world. For the uncorrupted youngster their teaching is all the more perplexing as, at the same time, the whole topic is presented as logical, systematic, reasonable, and precise. It would be nice to know in general which percentage of mathematical instruction is in fact usurped by getting pupils to learn how to live with notational anomalies; the percentage could very well be shockingly high. Another possibly heavy price is the widespread distortion of the general public’s view of mathematics.

• Parsing immediately becomes context-dependent, e.g.

                 p(x + y) .

Is this a product or a function application?

• It has created an awkward position for what are now known as reserved identifiers: what about

                 sin(s + i + n) ?

• It is undoubtedly responsible for the general reluctance to introduce multi-character identifiers, which after the exhaustion of the Latin alphabet led to using Greek letters, Gothic letters, Hebrew letters, and large script capitals. We need not elaborate on the ensuing cost and cumbersomeness of printing mathematical texts. This typographical immodesty, which makes many a typewriter all but useless, is the more amazing because it is of little help compared to the use of multi-character identifiers: the admission of two-character identifiers already gives the power of 52 new alphabets. (To be fair we should add that multi-character names have found their way into geometry to denote lines, line segments, triangles, etc. . Geometry is, of course, a context in which on dimensional grounds products are less common than quotients.)

• It is similarly responsible for the presence of many a subscript. It is not uncommon to see the angles of a triangle denoted by A1, A2, and A3, whereas A0, A1, and A2 would have done at least as nicely. Like the use of different alphabets, subscription is an unfortunate convention from a typographical point of view: it creates the need of a smaller character set or occasionally wider spacing of the lines.

• We shall deal with function application in a little more detail, since we might have readers that are unaware of the operator that has been omitted.

What is the quintessence of p being a function, say of a natural argument? Well, two things: firstly, that for natural variables x and y, say, we may write down p(x), p(y), p(x+y), etc. as legitimate expressions, and, secondly, that we can rely for all natural x and y on the validity of

x = y ⇛ p(x) = p(y) .

Our expressions p(x), p(x+y), etc. consist of two components, viz. the function – p in these cases – and a natural expression – x or x+y –. In mathematical parlance, in p(x), “x is supplied (as argument) to (the function) p” or alternatively “(the function) p is applied to (the argument) x”. In the notation used, this state of affairs has to be deduced from the succession of a function name and a parenthesized expression. (As pointed out before, whether this identification is context-dependent depends on the rest of the grammar, i.e. whether for instance the multiplication operator is invisible.) Note that this function notation extends the use of parentheses: as long as parentheses are used only as part of a convention that represents syntactic trees by strings, there is no need to surround a single variable by a pair of parentheses.

Consider next “the infinite sequence of natural numbers A0, A1, A2, ... ”. Then, for all natural i and j we may write down constructs like Ai, Aj, Ai+j. In short, in the position of the subscript we allow any natural expression (provided it is small enough). Also we can rely for all natural i and j on the validity of

i = j ⇛ Ai = Aj .

The moral of the story is that we have two different notations for the same state of affairs: function application tied p to x, y, and x+y in precisely the same way as subscription tied A to i, j, and i+j. It now stands to reason to consider a single operator to denote this connection, e.g. an infix period with the highest binding power of all. For our examples, this would give rise to the expressions

p.x, p.y, p.(x+y), A.i, A.j, A.(i+j) .

In the previous line the period is used as the visible representation of the operator known as “function application”.

In judging the pros and cons of this notational alternative, there is more to be considered than typographical simplification and greater notational or conceptual homogeneity. We should at least investigate the potential syntactic pitfalls of the new rendering of an expression such as fi(x), in which the old subscription and function notation are combined. We could encounter such an expression when dealing with a whole class of functions consisting of f0, f1, f2, ... . As we would now denote these functions by f.0, f.1, f.2, ... , a suitable candidate for fi(x) is

                 f.i.x .

But the period is not associative, so we have to settle how such a formula, if admitted, is to be parsed. Its non-admittance would imply the use of an obligatory parenthesis pair, yielding in this case (f.i).x, as in the alternative f.(i.x) we would encounter the non-interpretable subexpression i.x (i not denoting a function). Its admittance leaves the choice between context-dependent parsing or the strict rule that function application is left- (or right-) associative. In the case of context-dependent parsing, f.i.x would have to be parsed as (f.i).x, but p.A.i – for p and A defined earlier – would have to be parsed as p.(A.i). Though in a sufficiently typed context this convention does not lead to ambiguity, it has not been adopted, and probably wisely so. The usual choice, e.g. in functional programming, is left-associativity, i.e. admitting f.i.x, but requiring the parentheses in constructs like p.(A.i) and A.(A.i) or even A.(A.(A.i)). (In passing we note that traditional subscription is right-associative.)

It is interesting to note that purely notational considerations have led us to the discovery of the device known to the logicians as “Currying”, but for the judgement of notational adequacy there is more to be considered. Not only is it possible to distinguish between a function of two arguments and a function of one argument that happens to be a pair – vide f.i.x versus g.(x,y) –, but we also have to. In contexts in which this distinction is deemed irrelevant, the obligation to distinguish will be regarded as an awkward burden. On the other hand, it enables us to write down – using parentheses for list notation – expressions like sum.(a,b), sum(a,b,c), and even sum.(a) and sum.() without the introduction of a function with a variable number of arguments: they are all of the form sum.x where x is a list.

This seemed a suitable occasion for some experimental mathematics: in order to find out we carried out the experiment of adopting the infix period for function application. The initial experience was so favourable that at least some of our readers joined the experiment. The aforementioned obligation of distinction turned out to be less of a burden than expected. In a number of cases the possibility of distinguishing was essential; when at first sight the distinction seemed irrelevant, often closer inspection revealed one of the alternatives to be clearly preferable. The experiment continues, and the reader is invited to join it. (End of • .)

Historical remark. The decision to carry out the experiment was in part triggered by a rereading of the history of the equality sign. For three centuries after its introduction – by Robert Recorde in 1557 – the equality sign has not been recognized as a genuine infix operator, nor a = b as an expression. This had to wait until the introduction – by George Boole in 1854 – of the proper value domain of such expressions. And even then that recognition was slow to spread: to this very day the bulk of the mathematical literature treats the expression a = b as second-class citizen. The remarkable slowness of this process could very well be related to the fact that prior to Recorde equality, if not expressed verbally, was sometimes indicated by mere juxtaposition. (End of Historical remark.)

*                       *
*

We would like to stress the deficiency of notations in which identity or scope of dummies are unclear, because such notations are not uncommon.

For instance, we recall the set {j | (E i ∷ j = i2 ⋀ B.i)}. This is so clumsy that occasionally one finds this set denoted by {i2 | B.i}. Let us take, for the sake of the argument, a special choice for B, and consider the set denoted by {i2 | i > 2}; a similarly denoted set being {i3 | i > 3}, we find ourselves now considering

{ij | i > j} ,

and by that time we have been nicely led down the garden path. Had we written

{i : B.i : i2}

to start with – employing a notation that explicitly mentions the dummies in the position preceding the first colon – , we would have ended up with

{i : i > j : ij} ,

which definitely differs from

{i,j : i > j : ij} .

Remark. The above notation for sets has encountered the objection that it is unclear “how to read such a formula in normal English”. This is identical to the objection to the logical connective of equivalence, viz. that it defies smooth expression in all Western languages (do not forget that “if and only if” should be regarded as a linguistic artefact of the mathematicians). The objection is valid if we require our formalisms to mimic our verbal thinking. If freeing us from the shackles of our native tongues is viewed as one of the major virtues of formalisms, the above objections are no longer valid. (End of Remark.)

So much for the consequences of the obscurity of the dummy’s identity; let us now turn to its scope. One finds universal quantification denoted by prefixing with (∀x). Without explicitly stated priority rules, it is then no longer clear how to parse

(∀x)P.x ⋁ Q and (∀x)P.x ⋀ Q .

A possible reason why the parsing rules are often left undefined is that the two parsings

((∀x)P.x) ⋁ Q and (∀x)(P.x ⋁ Q)

of the first formula are semantically equivalent. Those of the second formula,

((∀x)P.x) ⋀ Q and (∀x)(P.x ⋀ Q) ,

are only equivalent if the range of x is nonempty; for an empty range they yield Q and true, respectively. These problems can be avoided by introducing an obligatory “parenthesis pair” that declares the dummy and delineates its scope (vide ALGOL 60’s block structure).

This is probably the place to point out that conjunction and disjunction are not the only symmetric and associative operators whose definition can be extended – sometimes conditionally – to a possibly infinite bag of operands; the maximum, the minimum, the sum, the product, and set formation come to mind. A homogeneous notation comprising (i) an explicit declaration of the dummies, (ii) a range expressed as a boolean expression in terms of the dummies, and (iii) a term expressed in terms of the dummies, might have avoided such anomalies as a traditional notation for summation

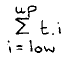
This notation erroneously ties the notation of summation to a range of consecutive integers, and the reader is invited to use it to express the sum of all prime numbers that are less than N.

There are two ways in which a homogeneous notation for quantified expressions could be used; in addition to being a tool for the working mathematician, it could be used as an educational device in order to separate the problem of how to use the dummies in quantified expressions from the problems caused by the irregularity and deficiences of established notations.

*                       *
*

In addition to the above, we have less grammatical concerns of notation. We mention the following ones.

• A notation should not force us to be explicit about what is irrelevant. In contexts in which lengths of strings are not very relevant, it is overspecific to represent them by the usual x1, x2, ..., xk. We have encountered cases where regular expressions provided the appropriate alternative. In other cases a combination of character variables x,y and string variables X,Y did the job: XxY stands for a nonempty string and x for one of its characters, xyX provides the nomenclature for the two leading elements of a string with at least two characters (and also for the possibly empty rest). Similarly, without a summation convention it is all but impossible to do analytical geometry without committing oneself to a specific dimension of the space in question. Coordinate-free analytical geometry provides many a nice example of arguments not encumbered by an arbitrarily chosen coordinate system.

• A notation should provide the combinatorial freedom we need. This does not only mean that what we would like to vary in the course of an argument should occur as an explicit parameter; it means more. We have mentioned the shortcomings of de Morgan’s notation for negation; we still find similar phenomena in much more recent literature, e.g. in R. Courant’s Differential and Integral Calculus:

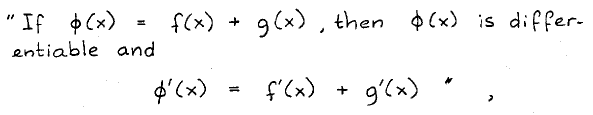
a roundabout way of expressing that differentiation distributes over addition. The formula (f + g)′ = f′ + g′ would have been much more direct, but Courant’s reluctance to introduce expressions whose values are functions forces him to introduce the name Φ, so as to have something to attach the prime to.

• Another way of losing combinatorial freedom is the introduction of a single character for the combination of two independent operations. An often observed example is the symbol ⊕ as in n ⊕ 1, for the addition reduced modulo some globally specified N. This is all right for 2n ⊕ 1, but the combined concept of addition modulo N is unfortunate: for 2n reduced modulo N it would lead to 2n ⊕ 0 or n ⊕ n. The introduction of ⊗ for multiplication reduced modulo N does not solve the problem but only pushes it forward: what about exponentiation?

We encounter the same loss of freedom when, in f = g, the equality sign is burdened with a universal quantification over the domain so as to express that f and g are the same function. It then becomes hard to express the boolean function that is true wherever f and g coincide and false elsewhere.

• We would like to point out that minor notational accidents can have major consequences. We give two examples.

We have all encountered and probably even used A = B = C to denote that A, B, and C are all equal. It is usually explained as a shorthand for A = B ⋀ B = C, transitivity supplying the remaining equality. But shorthands are dangerous: this one has generally obscured the fact that equality between boolean operands is not only symmetric but also associative. The truth of a continued boolean equality amounts to the number of false arguments being even, e.g. false = false = true, which may be parsed (false = false) = true or, alternatively, false = (false = true). We might consider a special symbol for that associative equality and write for boolean arguments for instance a ≡ b ≡ c. The irony of the situation is that indeed a special boolean equality sign is in use, but it is the wrong one with the wrong connotation: a ⇔ b, pronounced “a if and only if b”, is viewed as shorthand for a ⇒ b ⋀ b ⇒ a. As a result (a ⇔ b) ⇔ c and a ⇔ (b ⇔ c) have completely different expansions, and the associativity of boolean equality is hidden once more. But this is not the end of the sad story. General unfamiliarity with the algebraic properties of boolean equality (e.g. that furthermore disjunction distributes over it) has led to general underexploitation of it; as a result, proofs are often much longer than necessary. (Among electrical engineers it is not unusual to pronounce “≢” as “exclusive or”. How unfortunate this name is, surfaced during a lecture delivered for an American audience. When, in formalizing a specification, the audience was invited to supply the appropriate logical operator – which was the equivalence – someone suggested after some hesitation “the exclusive nor”!)

Next we mention the general acceptance of the symbol ⇒ for “implies”, more precisely the general absence of the symbol ⇐ for “is implied by” or “follows from”. We have seen a number of proofs in which the adherence to the implication sign gave rise to proofs that were in conflict with the convention that texts are best read from beginning to end: they were more conveniently read backwards. This observation invited the use of the follows-from symbol in a reverse presentation of the argument. It was a great improvement, as the switch from a bottom-up to a top-down argument enabled the enclusion of almost all heuristic considerations, which would have required an appeal to clairvoyance before. That the mere transition from ⇒ to ⇐ could have such a profound effect on mathematical exposition is a frightening observation, which is not to be forgotten. It is not impossible that the restriction to the one-sided ⇒ – inspired by the cause/effect dichotomy of the philosophers? – has greatly contributed to the mystification of mathematics. A sobering thought.

Acknowledgment. The Austin and Eindhoven Tuesday Afternoon Clubs are acknowledged for their constructive comments on an earlier version of this note. (End of Acknowledgment.)


Waalre, 27 January 1986


prof. dr. Edsger W. Dijkstra
Department of Computer Sciences
The University of Texas at Austin
Austin, TX 78712-1188
United States of America


drs. A.J.M. van Gasteren
BP Venture Research Fellow
Department of Mathematics and Computing Science
Eindhoven University of Technology
Postbus 513
5600 MB EINDHOVEN
The Netherlands