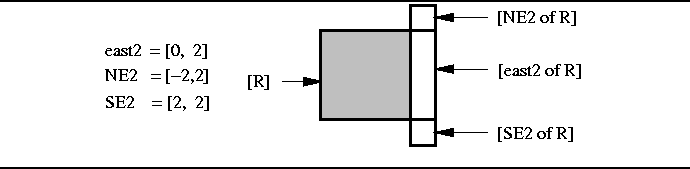
Figure 1: Illustration of ``Of'' Regions.
The Of operator takes two operands--a direction and a region--and evaluates to a region that is adjacent to the specified region. The relative position of the resulting region is determined by the signs of the components of the direction vector, and the size of the new region is determined by circumscribing a box around the direction as shown in Figure 1.

Figure 1: Illustration of ``Of'' Regions.
Mathematically, if vector vIn other words, ifand
region R
,
[v of R] defines an array of size
,
where
if
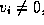
or
if
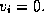
This array is located outside of R and adjacent to R at
,
where
if
,
if
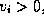
and
if